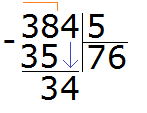
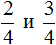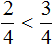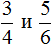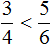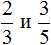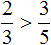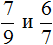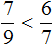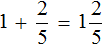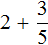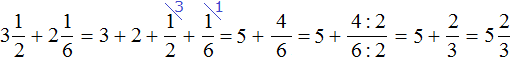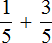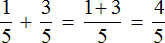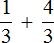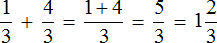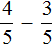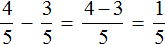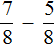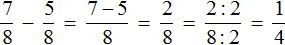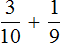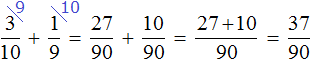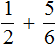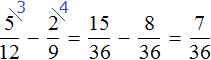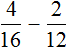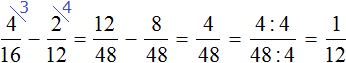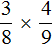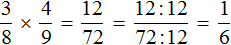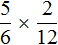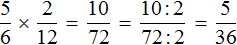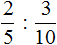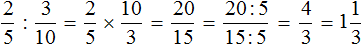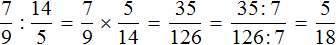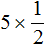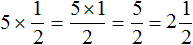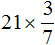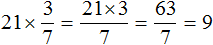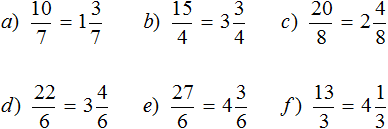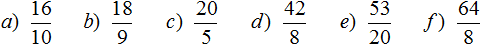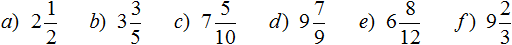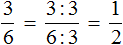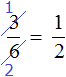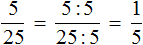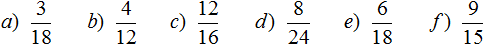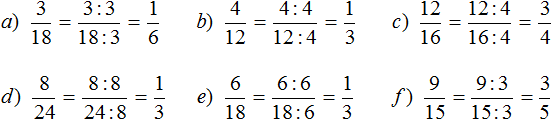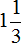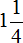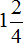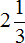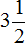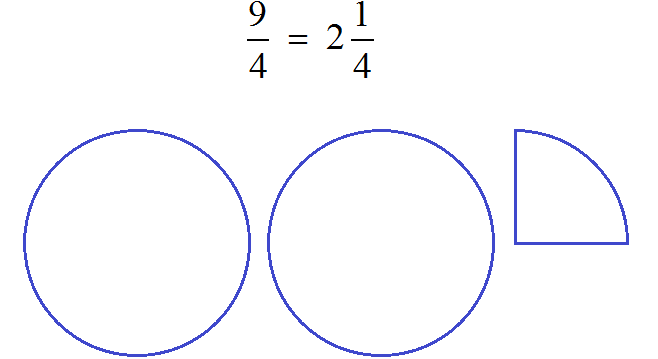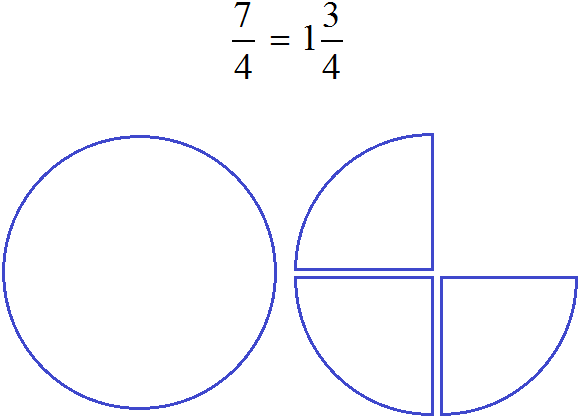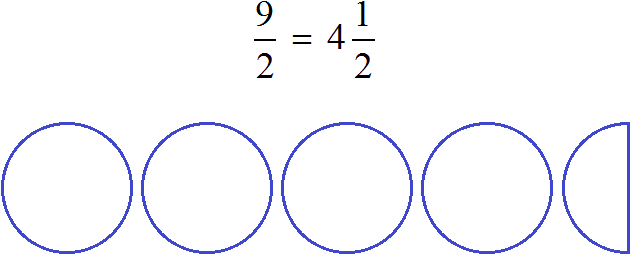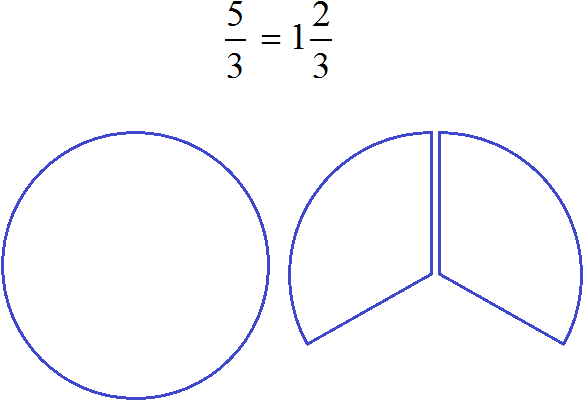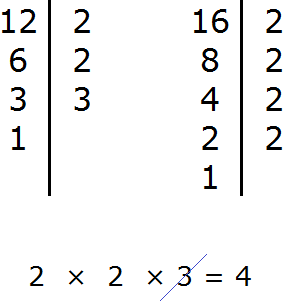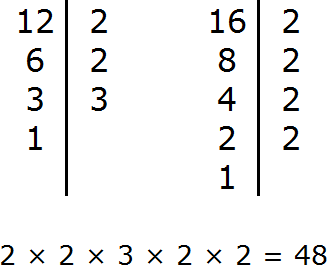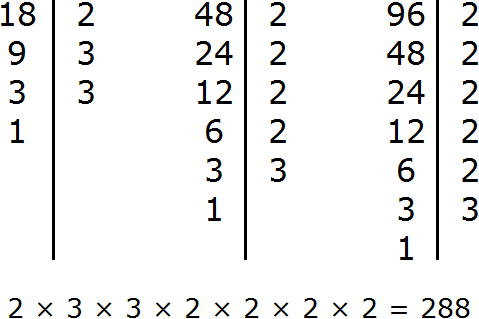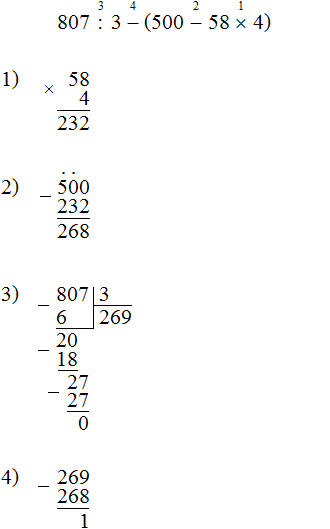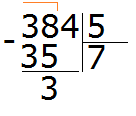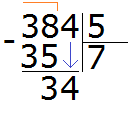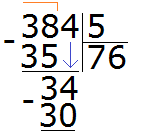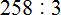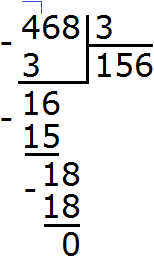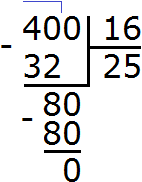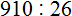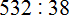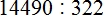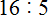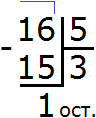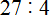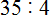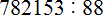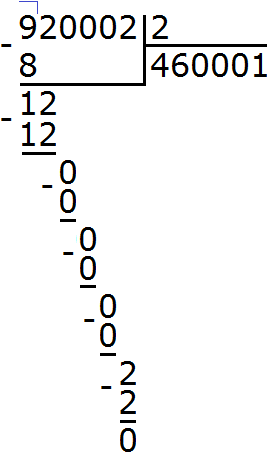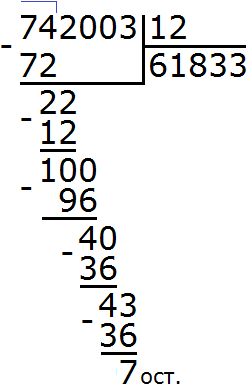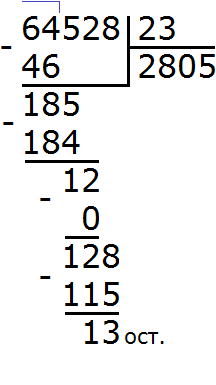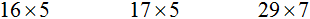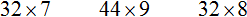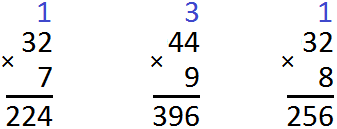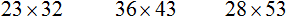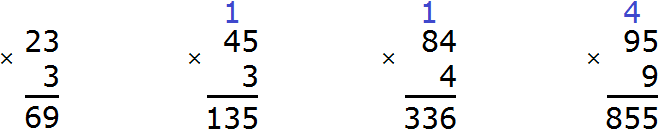Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше (<).
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Сравнение дробей с одинаковыми знаменателями
Дроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Например, сравним дроби ![]() и
и ![]() и ответим какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби
и ответим какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби ![]() числитель больше, чем у дроби
числитель больше, чем у дроби ![]() . Значит дробь
. Значит дробь ![]() больше, чем
больше, чем ![]() . Так и отвечаем. Отвечать нужно с помощью значка больше ( > )
. Так и отвечаем. Отвечать нужно с помощью значка больше ( > )
![]()
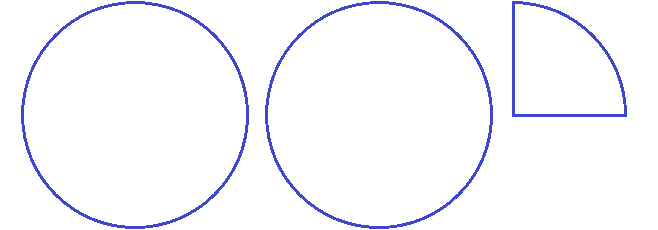
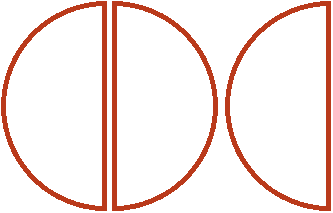
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. ![]() пиццы больше, чем
пиццы больше, чем ![]() пиццы:
пиццы:
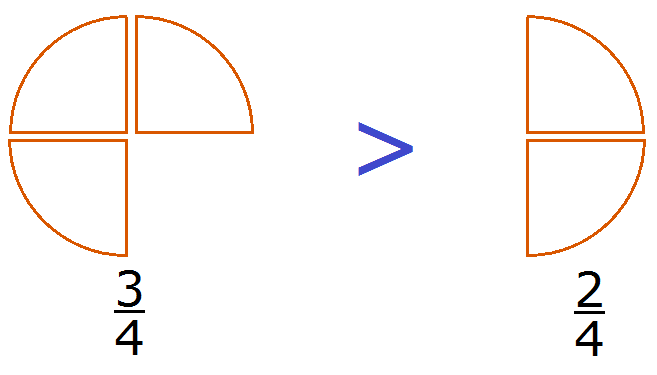
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителями
Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби ![]() и
и ![]() . У этих дробей одинаковые числители. У дроби
. У этих дробей одинаковые числители. У дроби ![]() знаменатель меньше, чем у дроби
знаменатель меньше, чем у дроби ![]() . Значит дробь
. Значит дробь ![]() больше, чем дробь
больше, чем дробь ![]() . Так и отвечаем:
. Так и отвечаем:![]()
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. ![]() пиццы больше, чем
пиццы больше, чем ![]() пиццы:
пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями. Например, сравнить дроби ![]() и
и .
Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби ![]() и
и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей
![]() и
и это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби ![]() . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
. НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
![]()
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
![]()
Умножим дроби на свои дополнительные множители:
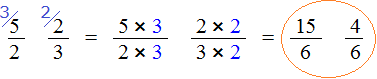
Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
![]()
Правило правилом, а мы попробуем разобраться почему ![]() больше, чем
больше, чем ![]() . Для этого выделим целую часть в неправильной дроби
. Для этого выделим целую часть в неправильной дроби ![]() . В дроби
. В дроби ![]() ничего выделять не нужно, поскольку эта дробь уже правильная.
ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби ![]() , получим следующее выражение:
, получим следующее выражение:
![]()
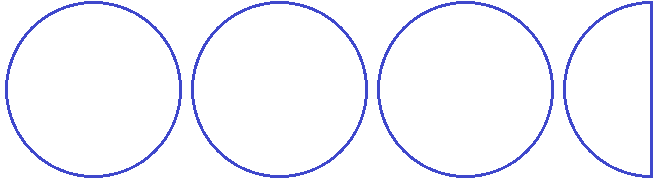
Теперь можно легко понять, почему ![]() больше, чем
больше, чем ![]() . Давайте нарисуем эти дроби в виде пицц:
. Давайте нарисуем эти дроби в виде пицц:
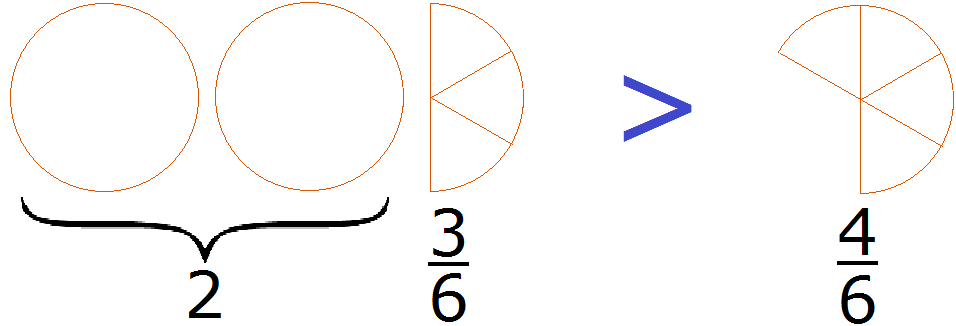
2 целые пиццы и ![]() пиццы, больше чем
пиццы, больше чем ![]() пиццы.
пиццы.
Вычитание смешанных чисел. Сложные случаи.
Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Например, 10 − 8 = 2
10 — уменьшаемое
8 — вычитаемое
2 — разность
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2
5 — уменьшаемое
7 — вычитаемое
−2 — разность
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример 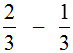 .
.
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. ![]() больше чем
больше чем ![]()
![]()
поэтому смело можем вернуться к примеру и решить его:
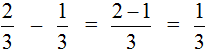
Теперь решим такой пример ![]()
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
![]()
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения ![]() .
.
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
![]()
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
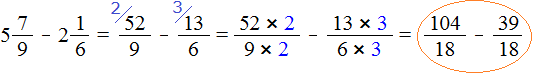
Теперь нужно сравнить дроби ![]() и
и ![]() . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
. Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби ![]() числитель больше, чем у дроби
числитель больше, чем у дроби ![]() . Значит дробь
. Значит дробь ![]() больше, чем дробь
больше, чем дробь ![]() .
.
![]()
А это значит что уменьшаемое ![]() больше, чем вычитаемое
больше, чем вычитаемое ![]()
![]()
А значит мы можем вернуться к нашему примеру и смело решить его:
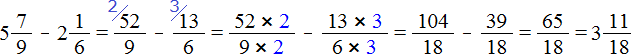
Пример 3. Найти значение выражения ![]()
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
![]()
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:
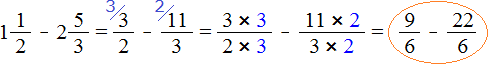
Теперь сравним дроби ![]() и
и ![]() . У дроби
. У дроби ![]() числитель меньше, чем у дроби
числитель меньше, чем у дроби ![]() , значит дробь
, значит дробь ![]() меньше, чем дробь
меньше, чем дробь ![]()
![]()
А это значит, что и уменьшаемое ![]() меньше, чем вычитаемое
меньше, чем вычитаемое ![]()
![]()
А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.
Пример 4. Найти значение выражения ![]()
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
![]()
Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:
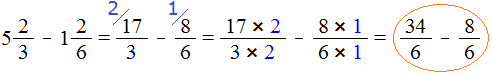
Теперь нужно сравнить дроби ![]() и
и ![]() . У дроби
. У дроби ![]() числитель больше, чем у дроби
числитель больше, чем у дроби ![]() . Значит дробь
. Значит дробь ![]() больше, чем дробь
больше, чем дробь ![]() .
.
![]()
А это значит, что уменьшаемое ![]() больше, чем вычитаемое
больше, чем вычитаемое ![]()
![]()
Поэтому мы смело можем продолжить вычисление нашего примера:
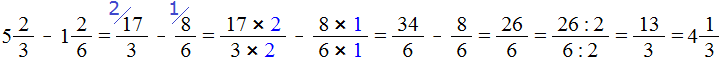
Сначала мы получили ответ ![]() . Эту дробь мы сократили на 2 и получили дробь
. Эту дробь мы сократили на 2 и получили дробь ![]() , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ
, но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ ![]() .
.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Смешанные числа
В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дроби
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь ![]() . Чтобы решить этот пример, нужно число 2 представить в виде дроби
. Чтобы решить этот пример, нужно число 2 представить в виде дроби ![]() . Затем сложить дроби с разными знаменателями:
. Затем сложить дроби с разными знаменателями:
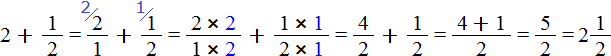
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: ![]() , а конец так:
, а конец так: ![]() . Различие в том, что в первом случае число 2 и дробь
. Различие в том, что в первом случае число 2 и дробь ![]() соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что
соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что ![]() это свёрнутая форма записи смешанного числа, а
это свёрнутая форма записи смешанного числа, а ![]() — развёрнутая.
— развёрнутая.
Когда перед нами смешанное число вида ![]() , мы должны понимать, что знак сложения опущен.
, мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения ![]() равно
равно ![]()
![]()
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
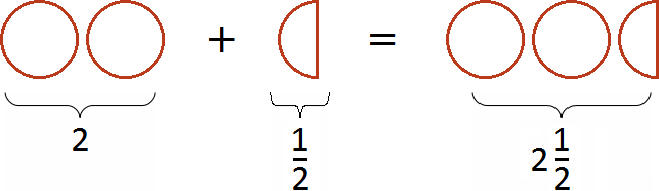
Пример 2. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем сложим дроби с разными знаменателями:
. Затем сложим дроби с разными знаменателями:
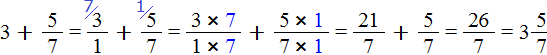
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
![]()
Пример 3. Найти значение выражения ![]()
Можно записать вместе число 2 и дробь ![]() , но этот ответ не будет окончательным, поскольку в дроби
, но этот ответ не будет окончательным, поскольку в дроби ![]() можно выделить целую часть.
можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби ![]() . Пять вторых это две целых и одна вторая:
. Пять вторых это две целых и одна вторая:
![]()
Теперь в главном выражении ![]() вместо дроби
вместо дроби ![]() запишем смешанное число
запишем смешанное число ![]()
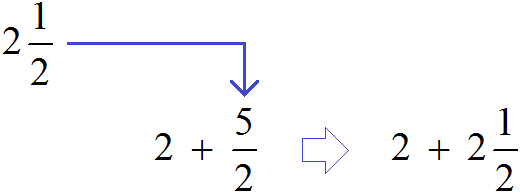
Получили новое выражение ![]() . В этом выражении смешанное число
. В этом выражении смешанное число ![]() запишем в развёрнутом виде:
запишем в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
![]()
Теперь свернём полученное смешанное число:
![]()
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
![]()
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения ![]() . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
. Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
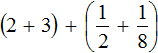
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
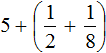
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
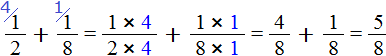
Получили ![]() . Теперь в главном выражении
. Теперь в главном выражении 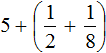 заменяем дробные части на полученную дробь
заменяем дробные части на полученную дробь ![]()
![]()
Теперь свернем полученное смешанное число:
![]()
Таким образом, значение выражения ![]() равно
равно ![]() . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
. Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
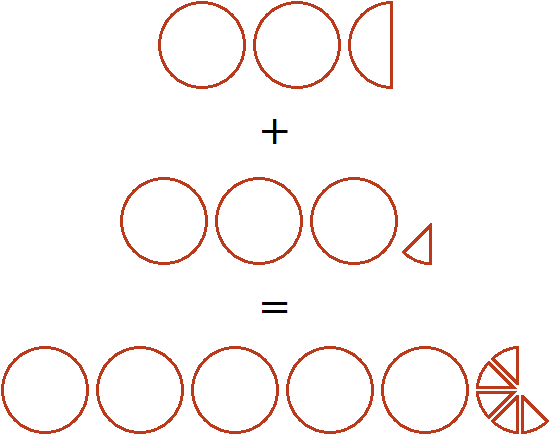
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
![]()
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
![]()
Сгруппируем целые и дробные части по отдельности:
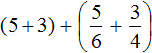
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
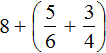
Теперь вычислим дробные части:
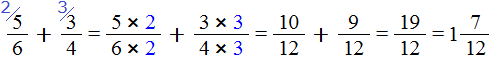
Получили смешанное число ![]() . Теперь в главном выражении
. Теперь в главном выражении 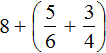 заменяем выражение в скобках на полученное смешанное число
заменяем выражение в скобках на полученное смешанное число ![]()
![]()
Получили выражение ![]() . В данном случае число 8 надо прибавить к целой части смешанного числа
. В данном случае число 8 надо прибавить к целой части смешанного числа ![]() . Для этого смешанное число
. Для этого смешанное число ![]() можно временно развернуть, чтобы было понятнее, что с чем складывать:
можно временно развернуть, чтобы было понятнее, что с чем складывать:
![]()
Сложим целые части. Получаем 9
![]()
Сворачиваем готовый ответ:
![]()
Таким образом, значение выражения равно
![]() .
.
Полное решение этого примера выглядит следующим образом:
![]()
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения ![]()
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
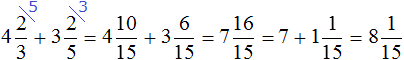
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число ![]() . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
. В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
![]()
Здесь смешанная дробь ![]() была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ
была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ ![]() .
.
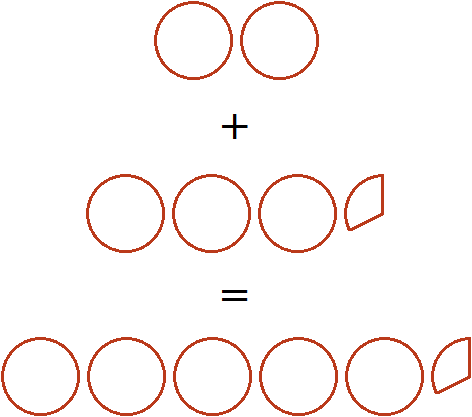
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Пример 2. Найти значение выражения ![]()
В этом примере, как и в предыдущем, нужно сложить целые части:
![]()
Осталось свернуть целую и дробную части, но дело в том, что дробная часть ![]() представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
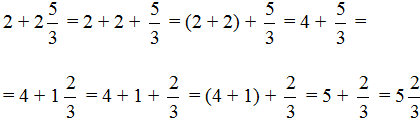
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь ![]() . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби
. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби ![]() , и выполнить вычитание дробей с разными знаменателями:
, и выполнить вычитание дробей с разными знаменателями:
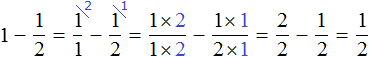
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
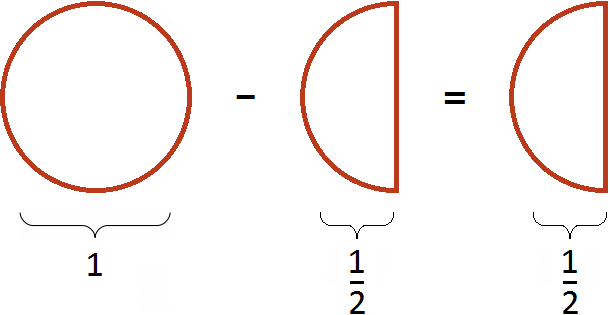
Пример 2. Найти значение выражения ![]() .
.
Представим число 2 в виде дроби ![]() , и выполним вычитание дробей с разными знаменателями:
, и выполним вычитание дробей с разными знаменателями:
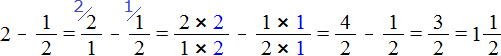
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
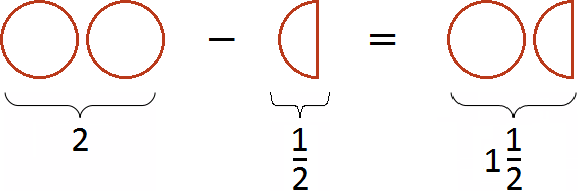
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения ![]() , не приводя на бумаге никаких вычислений.
, не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:

Нужно вычесть из них ![]() . Мы помним, что треть выглядит следующим образом:
. Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось ![]() (две целых и две трети пиццы).
(две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения ![]() обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
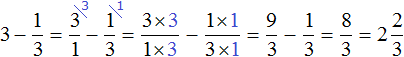
Пример 3. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем выполним вычитание дробей с разными знаменателями:
. Затем выполним вычитание дробей с разными знаменателями:
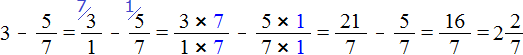
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа
в неправильную дробь, получим дробь
![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
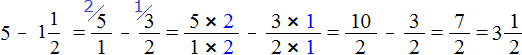
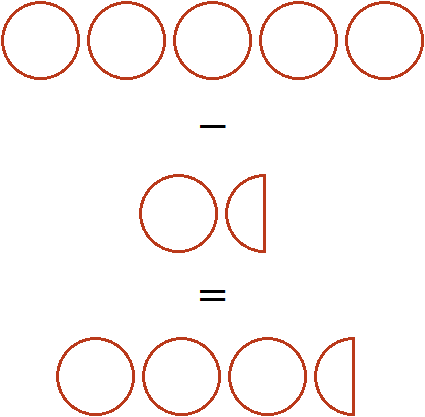
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения ![]()
Представим 6 в виде дроби ![]() , а смешанное число
, а смешанное число ![]() , в виде неправильной дроби. После перевода смешанного числа
, в виде неправильной дроби. После перевода смешанного числа ![]() в неправильную дробь, получим дробь
в неправильную дробь, получим дробь ![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
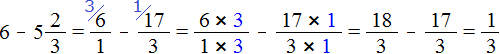
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения ![]() , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
, то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

Тогда от той пиццы, от которой отрезали останется
![]() пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
![]()
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения: ![]()
Чтобы решить этот пример, нужно смешанные числа ![]() и
и ![]() перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
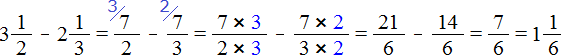
Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
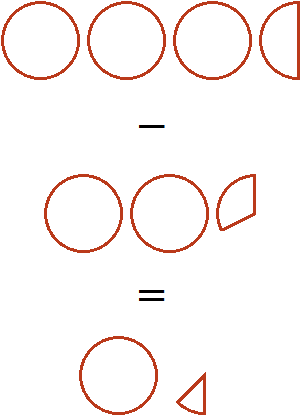
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа ![]() и
и ![]() в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь ![]() . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби ![]() , а знаменатель оставить без изменения:
, а знаменатель оставить без изменения:
![]()
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
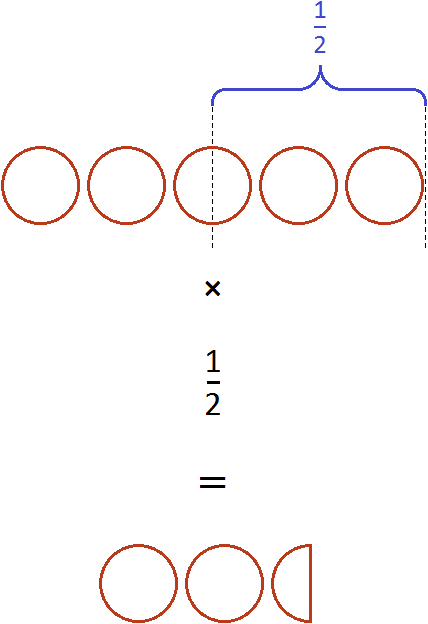
Пример 2. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
В ответе получилась неправильная дробь ![]() , но мы выделили её целую часть и получили 2.
, но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
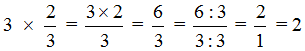
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
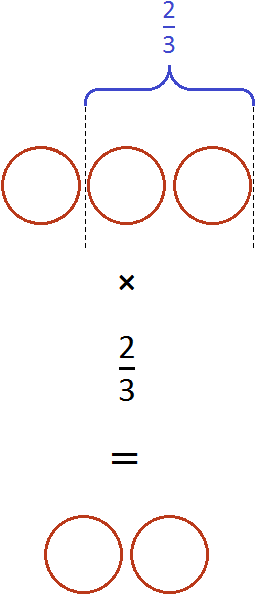
Пример 3. Найти значение выражения ![]()
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
![]()
Пример 4. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения ![]()
Переведём смешанное число ![]() в неправильную дробь. После перевода это число превратится в дробь
в неправильную дробь. После перевода это число превратится в дробь ![]() . Затем можно будет умножить эту дробь на
. Затем можно будет умножить эту дробь на
![]()
Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
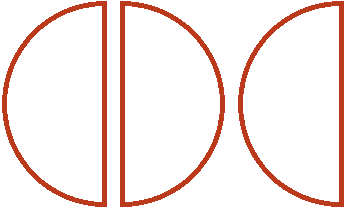
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
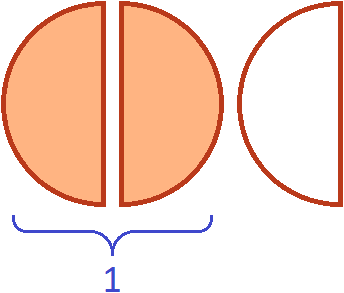
Поэтому значение выражения ![]() было равно 1
было равно 1
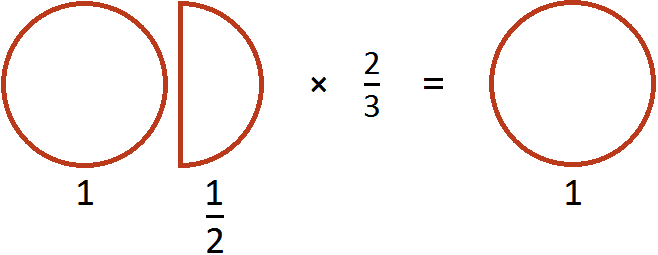
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить ![]() и
и ![]() . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
. Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
![]()
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
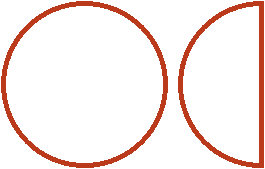
Теперь разберемся со смешанным множителем ![]() . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще
. Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще ![]() раза.
раза.
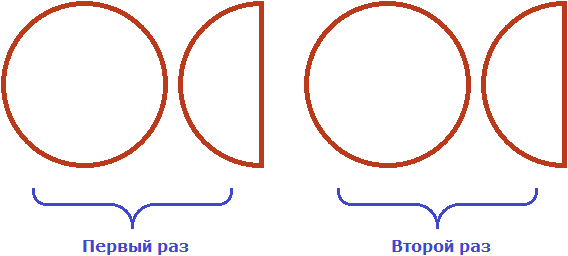
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
Но ещё осталось взять ![]() от изначальной целой пиццы и половины, ведь множителем было смешанное число
от изначальной целой пиццы и половины, ведь множителем было смешанное число ![]() . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
. Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
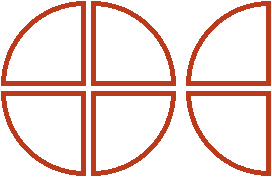
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
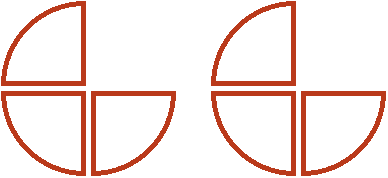
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения ![]() равно
равно ![]()
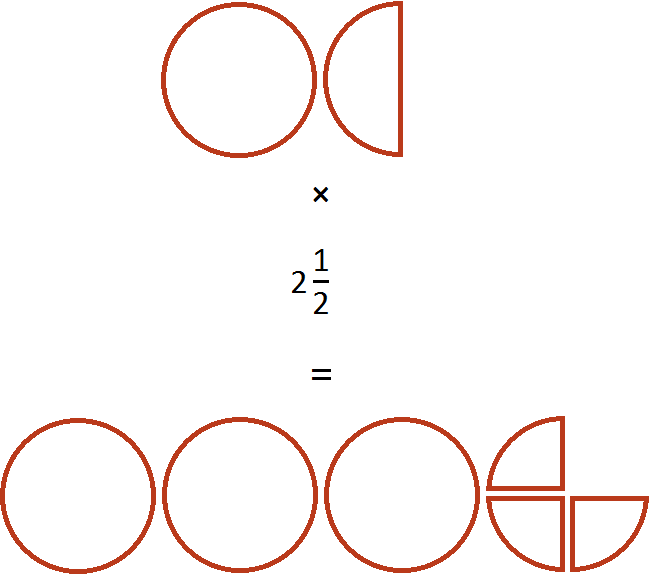
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
![]()
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь ![]() . Здесь число 3 — это делимое, а дробь
. Здесь число 3 — это делимое, а дробь ![]() — делитель.
— делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 3 на дробь
. Поэтому умножаем число 3 на дробь ![]()
![]()
Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз ![]() (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
(половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
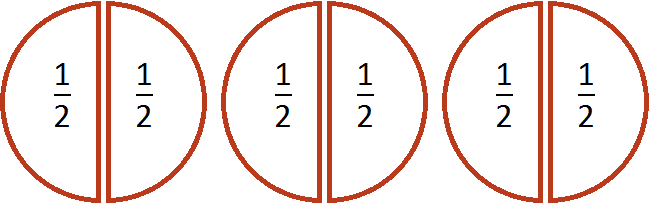
Поэтому значение выражения ![]() равно 6.
равно 6.
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби
пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби ![]() . После выделения целой части в этой дроби получим
. После выделения целой части в этой дроби получим ![]()
Теперь поставим вопрос так: «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух пиццах?».
(одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
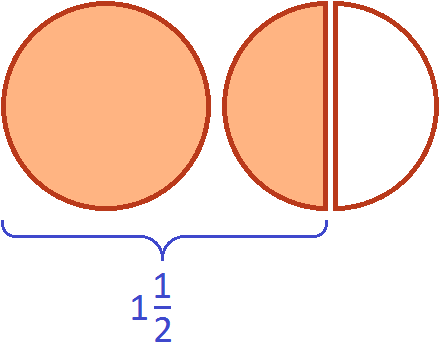
А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения ![]() равно
равно ![]()
Пример 3. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 5 на
. Поэтому умножаем число 5 на ![]()
![]()
Дробь ![]() это 2 целых и
это 2 целых и ![]() . Проще говоря, две целые и четверть пиццы:
. Проще говоря, две целые и четверть пиццы:

А выражение ![]() определяет сколько раз
определяет сколько раз ![]() содержится в пяти целых пиццах. Ответом было смешанное число
содержится в пяти целых пиццах. Ответом было смешанное число ![]() .
.
То есть ![]() пиццы содержится в пяти целых пиццах
пиццы содержится в пяти целых пиццах ![]() раза.
раза.
Давайте нащупаем в пяти пиццах два раза по ![]()
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой ![]() от
от ![]() , которые не вместились. Двумя девятыми они являются по той причине, что в
, которые не вместились. Двумя девятыми они являются по той причине, что в ![]() пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
Поэтому значение выражения ![]() равно
равно ![]()
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь ![]() на число 2
на число 2
Чтобы разделить дробь ![]() на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь ![]()
![]()
Пусть имеется половина пиццы:

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно дробь ![]() умножить на число, обратное числу 2. Обратное числу 2 это дробь
умножить на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Пример 3. Найти значение выражения ![]()
Умножаем первую дробь ![]() на число, обратное числу 3. Обратное числу 3 это дробь
на число, обратное числу 3. Обратное числу 3 это дробь ![]()
![]()
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на ![]() .
.
Чтобы решить этот пример, нужно делитель ![]() перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Затем умножим 2 на дробь, обратную дроби
. Затем умножим 2 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
(одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Переводим делитель ![]() в неправильную дробь, получаем
в неправильную дробь, получаем ![]() . Теперь умножаем число 5 на дробь, обратную дроби
. Теперь умножаем число 5 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь ![]()
![]()
Сначала мы получили ответ ![]() , затем сократили эту дробь на 5, и получили
, затем сократили эту дробь на 5, и получили ![]() , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
, но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ ![]()
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим ![]() на 2. Чтобы решить этот пример, нужно делимое
на 2. Чтобы решить этот пример, нужно делимое ![]() перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() .
.
Теперь умножаем ![]() на число, обратное числу 2. Обратное числу 2 это дробь
на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
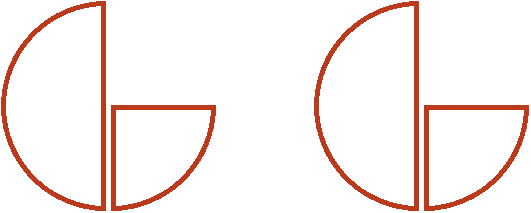
Поэтому значение выражения ![]() равно
равно
Пример 2. Найти значение выражения ![]()
Переведём делимое ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Теперь умножаем
. Теперь умножаем ![]() на число, обратное числу 4. Обратное числу 4 это дробь
на число, обратное числу 4. Обратное числу 4 это дробь ![]() .
.
![]()
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Как решать дальше мы уже знаем. Первую дробь ![]() нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь
нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь ![]() .
.
Дорешаем данный пример до конца:
![]()
Допустим, имеются две целые и половина пиццы:
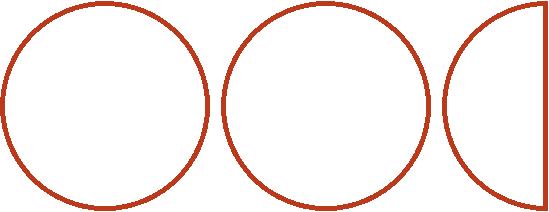
Если зададим вопрос «Сколько раз ![]() (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
(одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
Пример 2. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь ![]()
![]()
Сначала мы получили дробь![]() . Эту дробь мы сократили на 9. В результате получили дробь
. Эту дробь мы сократили на 9. В результате получили дробь ![]() , но такой ответ нас тоже не устроил и мы выделили в дроби
, но такой ответ нас тоже не устроил и мы выделили в дроби ![]() целую часть. В результате получили окончательный ответ
целую часть. В результате получили окончательный ответ ![]() .
.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателями
Сложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
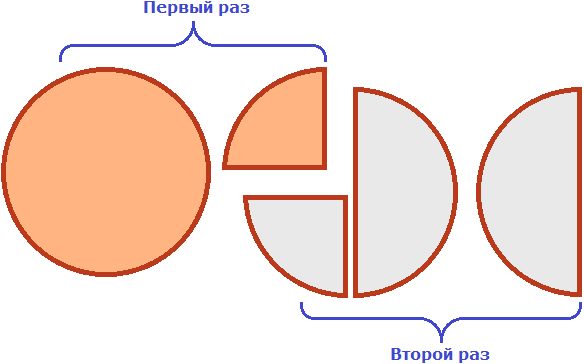
Например, слóжим дроби ![]() и
и ![]() . Складываем числители, а знаменатель оставляем без изменения:
. Складываем числители, а знаменатель оставляем без изменения:
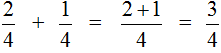
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к ![]() пиццы прибавить
пиццы прибавить ![]() пиццы, то получится
пиццы, то получится ![]() пиццы:
пиццы:
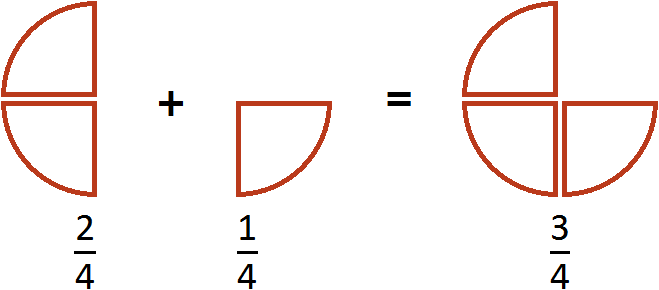
Пример 2. Сложить дроби ![]() и
и ![]() .
.
Опять же складываем числители, а знаменатель оставляем без изменения:
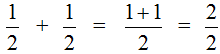
В ответе получилась неправильная дробь ![]() . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
. Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
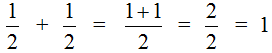
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к ![]() пиццы прибавить еще
пиццы прибавить еще ![]() пиццы, то получится одна целая пицца:
пиццы, то получится одна целая пицца:
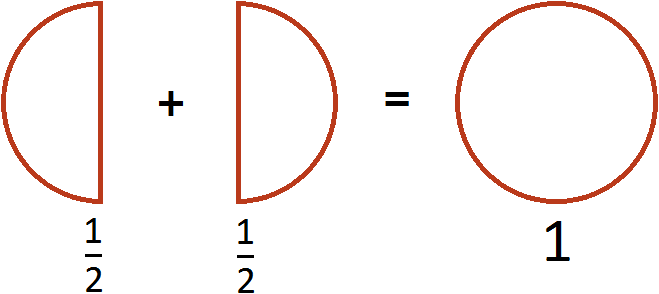
Пример 3. Сложить дроби ![]() и
и ![]() .
.
Опять же складываем числители, а знаменатель оставляем без изменения:
![]()
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к ![]() пиццы прибавить ещё
пиццы прибавить ещё ![]() пиццы, то получится
пиццы, то получится ![]() пиццы:
пиццы:
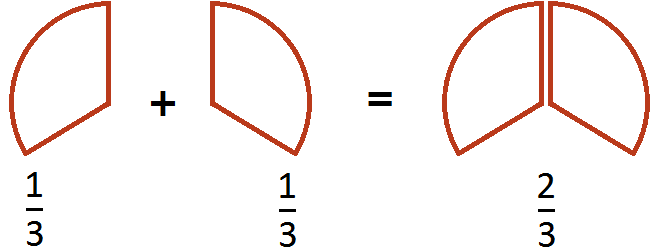
Пример 4. Найти значение выражения 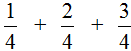
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
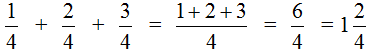
Попробуем изобразить наше решение с помощью рисунка. Если к ![]() пиццы прибавить
пиццы прибавить ![]() пиццы и ещё прибавить
пиццы и ещё прибавить пиццы, то получится 1 целая и ещё
![]() пиццы.
пиццы.

Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби ![]() и
и ![]() сложить можно, поскольку у них одинаковые знаменатели.
сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби ![]() и
и ![]() сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
![]()
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и
![]() . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
. Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
![]()
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
![]()
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
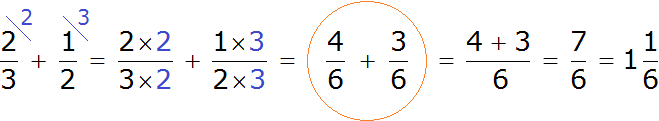
Таким образом, пример завершается. К прибавить
![]() получается
получается ![]() .
.
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить
![]() пиццы, то получится одна целая пицца и еще одна шестая пиццы:
пиццы, то получится одна целая пицца и еще одна шестая пиццы:
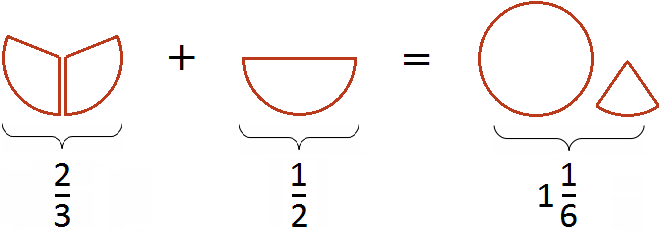
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и
![]() к общему знаменателю, мы получили дроби
к общему знаменателю, мы получили дроби ![]() и
и ![]() . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
. Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
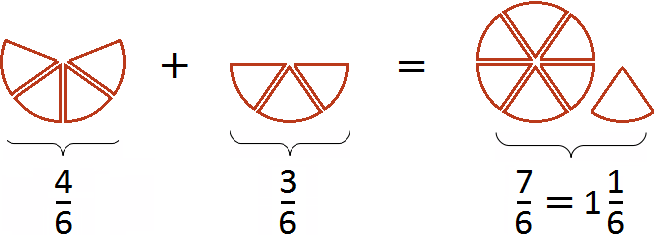
Первый рисунок изображает дробь ![]() (четыре кусочка из шести), а второй рисунок изображает дробь
(четыре кусочка из шести), а второй рисунок изображает дробь ![]() (три кусочка из шести). Сложив эти кусочки мы получаем
(три кусочка из шести). Сложив эти кусочки мы получаем ![]() (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили
(семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили ![]() (одну целую пиццу и еще одну шестую пиццы).
(одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
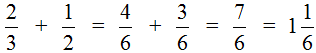
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения 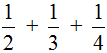 .
.
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
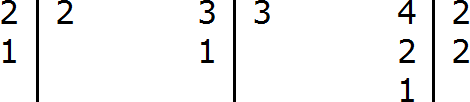
![]()
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
![]()
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
![]()
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
![]()
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
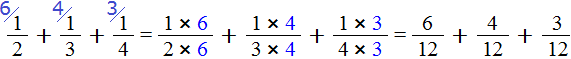
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
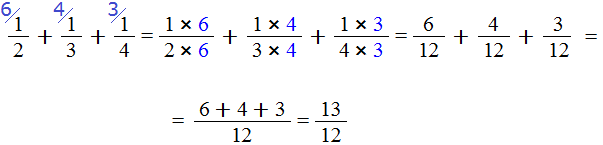
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
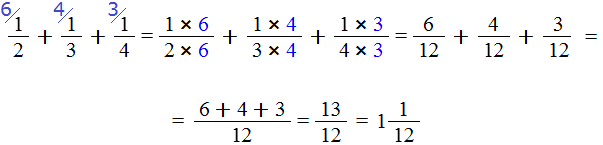
Получили ответ ![]()
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения 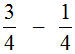 . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
. Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
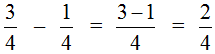
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от ![]() пиццы отрезать
пиццы отрезать ![]() пиццы, то получится
пиццы, то получится ![]() пиццы:
пиццы:
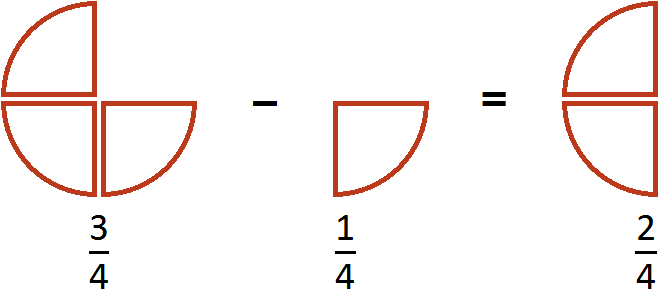
Пример 2. Найти значение выражения 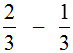 .
.
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
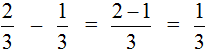
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от ![]() пиццы отрезать
пиццы отрезать ![]() пиццы, то получится
пиццы, то получится ![]() пиццы:
пиццы:
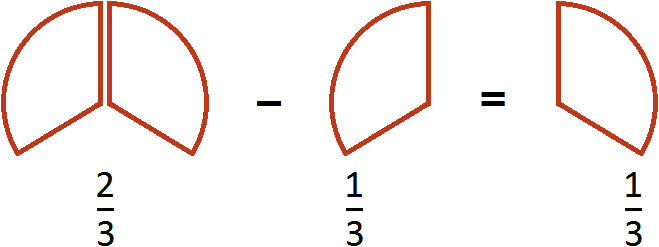
Пример 3. Найти значение выражения 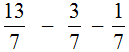
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
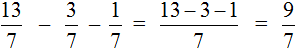
В ответе получилась неправильная дробь. Выделим в ней целую часть:
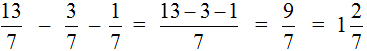
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби ![]() можно вычесть дробь
можно вычесть дробь ![]() , поскольку у этих дробей одинаковые знаменатели. А вот от дроби
, поскольку у этих дробей одинаковые знаменатели. А вот от дроби ![]() нельзя вычесть дробь
нельзя вычесть дробь ![]() , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения: 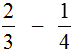
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям ![]() и
и ![]()
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
![]()
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
![]()
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
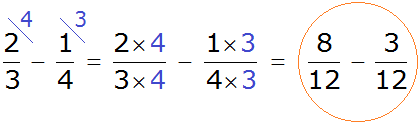
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
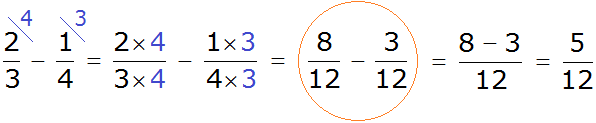
Получили ответ ![]()
Попробуем изобразить наше решение с помощью рисунка. Если от ![]() пиццы отрезать
пиццы отрезать ![]() пиццы, то получится
пиццы, то получится ![]() пиццы
пиццы
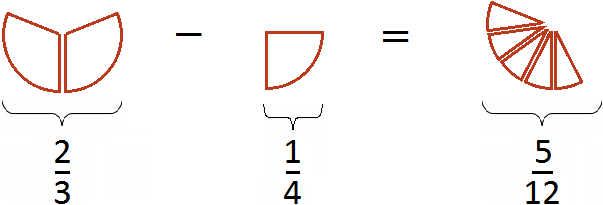
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
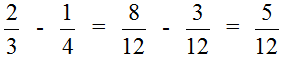
Приведение дробей ![]() и
и ![]() к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби
к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби ![]() и
и ![]() . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
. Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
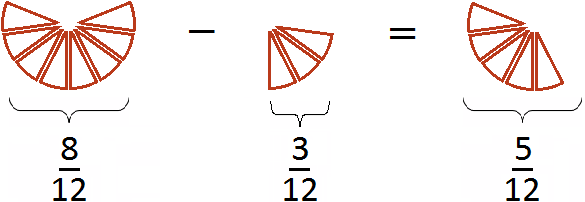
Первый рисунок изображает дробь ![]() (восемь кусочков из двенадцати), а второй рисунок — дробь
(восемь кусочков из двенадцати), а второй рисунок — дробь ![]() (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь
(три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь ![]() и описывает эти пять кусочков.
и описывает эти пять кусочков.
Пример 2. Найти значение выражения 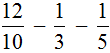
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
![]()
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
![]()
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
![]()
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
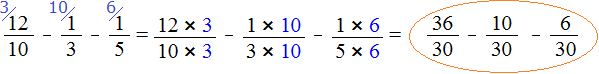
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
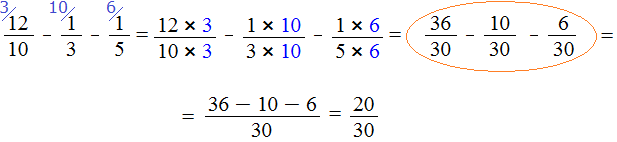
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь ![]() , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
, нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
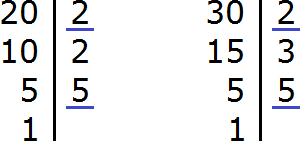
![]()
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби ![]() на найденный НОД, то есть на 10
на найденный НОД, то есть на 10
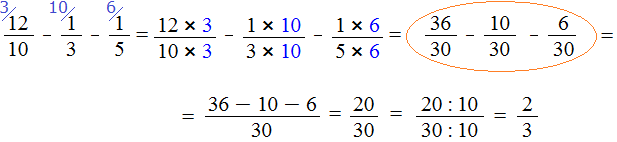
Получили ответ ![]()
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь ![]() на число 1.
на число 1.
Умножим числитель дроби ![]() на число 1
на число 1
![]()
Запись ![]() можно понимать, как взять половину 1 раз. К примеру, если
можно понимать, как взять половину 1 раз. К примеру, если ![]() пиццы взять 1 раз, то получится
пиццы взять 1 раз, то получится ![]() пиццы
пиццы
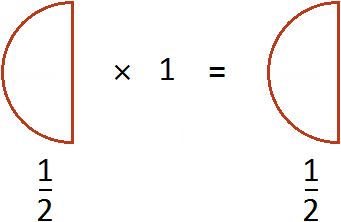
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение ![]() , записать как
, записать как ![]() , то произведение по прежнему будет равно
, то произведение по прежнему будет равно ![]() . Опять же срабатывает правило перемножения целого числа и дроби:
. Опять же срабатывает правило перемножения целого числа и дроби:
![]()
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется ![]() пиццы:
пиццы:
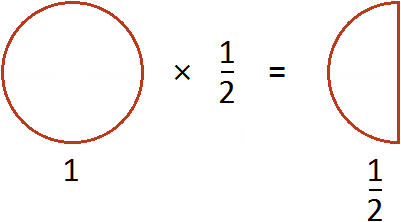
Пример 2. Найти значение выражения ![]()
Умножим числитель дроби ![]() на 4
на 4
![]()
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Выражение ![]() можно понимать, как взятие двух четвертей 4 раза. К примеру, если
можно понимать, как взятие двух четвертей 4 раза. К примеру, если ![]() пиццы взять 4 раза, то получится две целые пиццы
пиццы взять 4 раза, то получится две целые пиццы
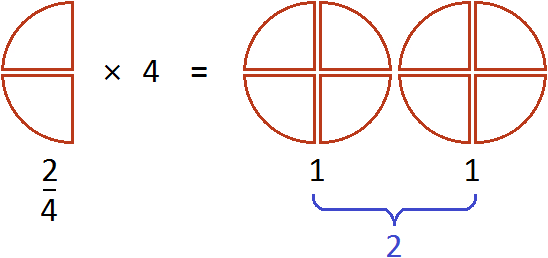
А если поменять множимое и множитель местами, то получим выражение ![]() . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
. Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
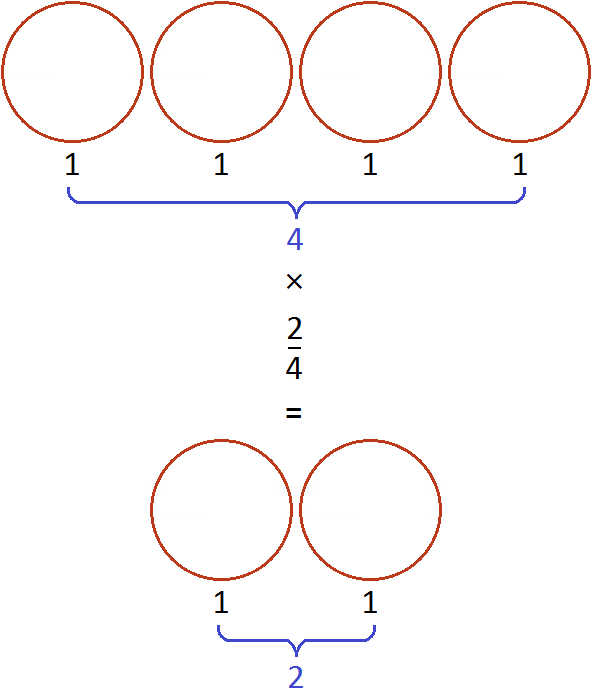
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение ![]() можно вычислить двумя способами.
можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
![]()
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
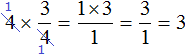
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
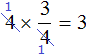
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
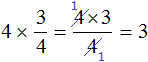
А вот к примеру выражение ![]() можно вычислить только первым способом — умножить число 7 на числитель дроби
можно вычислить только первым способом — умножить число 7 на числитель дроби ![]() , а знаменатель оставить без изменений:
, а знаменатель оставить без изменений:
![]()
Связано это с тем, что число 7 и знаменатель дроби ![]() не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
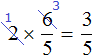
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением 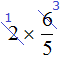 деление выполнено только в числителе, поскольку записать
деление выполнено только в числителе, поскольку записать 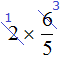 это всё равно, что записать
это всё равно, что записать 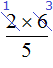 . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
. Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения ![]() .
.
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
![]()
Получили ответ ![]() . Желательно сократить данную дробь. Дробь
. Желательно сократить данную дробь. Дробь ![]() можно сократить на 2. Тогда окончательное решение примет следующий вид:
можно сократить на 2. Тогда окончательное решение примет следующий вид:
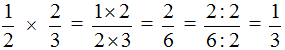
Выражение ![]() можно понимать, как взятие
можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:

Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:

И взять от этих трех кусочков два:
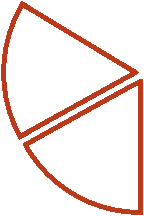
У нас получится ![]() пиццы. Вспомните, как выглядит пицца, разделенная на три части:
пиццы. Вспомните, как выглядит пицца, разделенная на три части:

Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
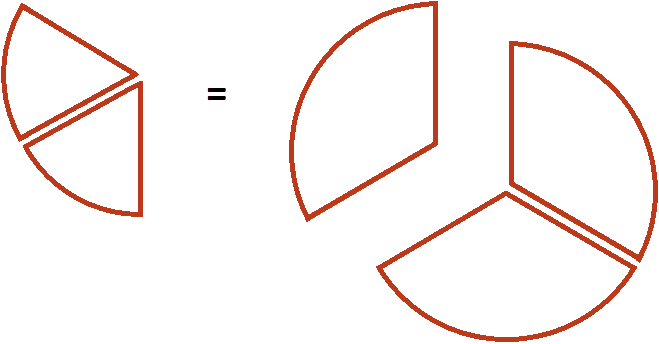
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения ![]() равно
равно ![]()
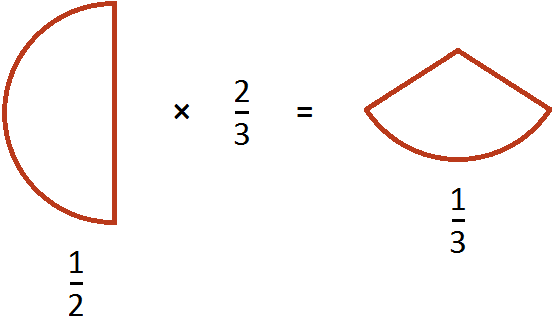
Пример 2. Найти значение выражения ![]()
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
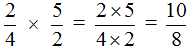
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Пример 3. Найти значение выражения ![]()
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
![]()
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
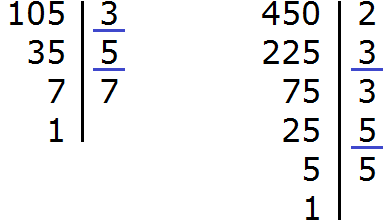
![]()
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
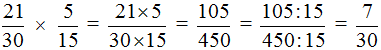
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как ![]() . От этого пятёрка своего значения не поменяет, поскольку выражение
. От этого пятёрка своего значения не поменяет, поскольку выражение ![]() означает «число пять разделить на единицу», а это, как известно равно пятёрке:
означает «число пять разделить на единицу», а это, как известно равно пятёрке:
![]()
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
![]()
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь ![]() на саму себя, только перевёрнутую:
на саму себя, только перевёрнутую:
![]()
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
![]()
Значит обратным к числу 5, является число ![]() , поскольку при умножении 5 на
, поскольку при умножении 5 на ![]() получается единица.
получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь

- обратным числа 3 является дробь

- обратным числа 4 является дробь

Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
- для дроби
 обратной дробью является дробь
обратной дробью является дробь 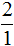
- для для дроби
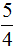 обратной дробью является дробь
обратной дробью является дробь 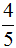
- для дроби
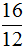 обратной дробью является дробь
обратной дробью является дробь 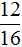
Деление дроби на число
Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?
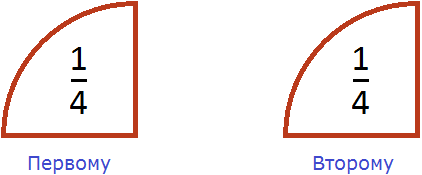
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет ![]() пиццы. Значит каждому достанется по
пиццы. Значит каждому достанется по ![]() пиццы.
пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь ![]() на число 2. Здесь делимым является дробь
на число 2. Здесь делимым является дробь ![]() , а делителем число 2.
, а делителем число 2.
Чтобы разделить дробь ![]() на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь
на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь ![]() . Значит нужно умножить
. Значит нужно умножить ![]() на
на ![]()
![]()
Получили ответ ![]() . Значит при делении половины на две части получается четверть.
. Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь ![]()
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить ![]() на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь ![]()
Пример 2. Найти значение выражения ![]()
Умножим первую дробь на число, обратное делителю:
![]()
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
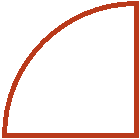
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь ![]()
![]()
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения ![]()
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
![]()
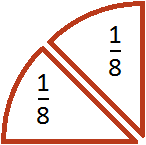
Допустим, имелось ![]() пиццы:
пиццы:

Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет ![]() . Поэтому при делении
. Поэтому при делении ![]() на 6 получается
на 6 получается ![]()
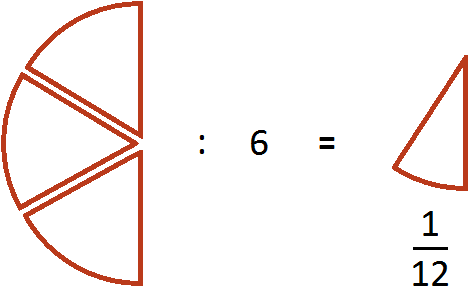
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на ![]() .
.
Чтобы разделить число 1 на ![]() , нужно это число 1 умножить на дробь, обратную дроби
, нужно это число 1 умножить на дробь, обратную дроби ![]() . А обратная дроби
. А обратная дроби ![]() это дробь
это дробь ![]()
![]()
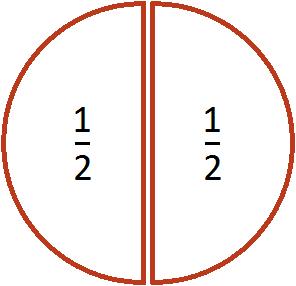
Выражение ![]() можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:

Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражения ![]()
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь ![]()
![]()
Допустим, у нас имеются две целые пиццы:
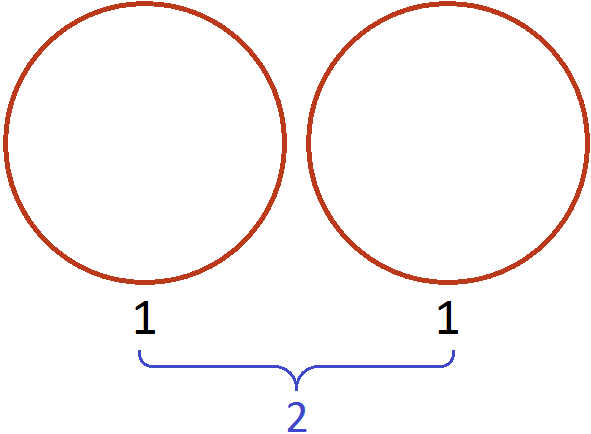
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
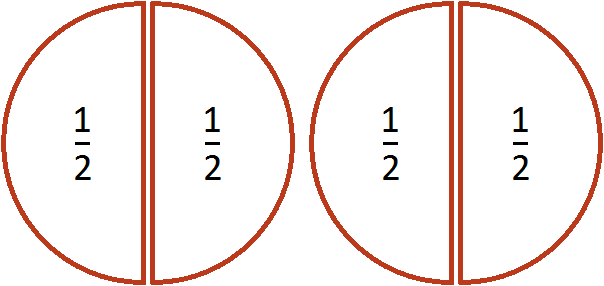
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим ![]() на
на ![]()
Чтобы разделить ![]() на
на ![]() , нужно
, нужно ![]() умножить на дробь, обратную дроби
умножить на дробь, обратную дроби ![]() . А обратная дроби
. А обратная дроби ![]() это дробь
это дробь ![]()
![]()
Допустим, имеется половина пиццы:

Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
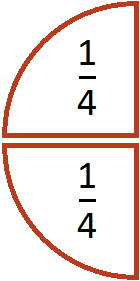
Пример 1. Найти значение выражения ![]()
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
![]()
Пример 2. Найти значение выражения ![]()
Умножаем первую дробь на дробь обратную второй:
![]()
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Дроби
Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.
Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.
А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.
Что такое дробь?
Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.
Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.

Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:
![]()
Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
![]()
А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
![]()
Такие записи называют дробями. Дробь состоит из числителя и знаменателя.
Число, которое записывается сверху, называется числителем дроби.
Число, которое записывается снизу, называется знаменателем дроби.
В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.
Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?
Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):
![]()
Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».
Теперь представьте, что пиццу мы разделили не на четыре части, а на три.

Допустим мы съели один кусок этой пиццы. Как записать такую дробь?
Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:
![]()
Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».
Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:
![]()
Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:

Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?
Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:
![]()
Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».
Дроби, которые мы сейчас рассмотрели, называют обыкновенными.
Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.
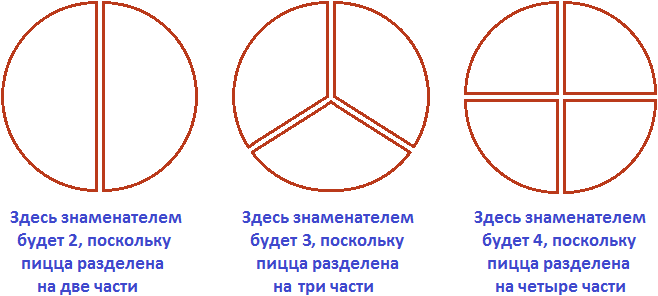
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли ![]() (одну часть из двух), или как говорят в народе «половину» пиццы.
(одну часть из двух), или как говорят в народе «половину» пиццы.
С помощью переменных дробь можно записать так:
![]() где a — это числитель, b — знаменатель.
где a — это числитель, b — знаменатель.
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
![]()
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём ![]() (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
(одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
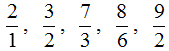 Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Теперь возьмём к примеру неправильную дробь ![]() и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:
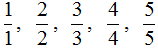
Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь ![]() . Применим её к нашей пицце.
. Применим её к нашей пицце.
Допустим, мы хотим съесть![]() пиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим эту
пиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим эту![]() пиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
пиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Дробь означает деление
Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь ![]() . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
. Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
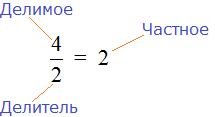
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
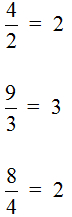
Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».
Выделение целой части дроби
Вычислим дробь ![]() . Пять разделить на два будет два и один в остатке:
. Пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Проверка: (2 × 2) + 1 = 4 + 1 = 5
Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:
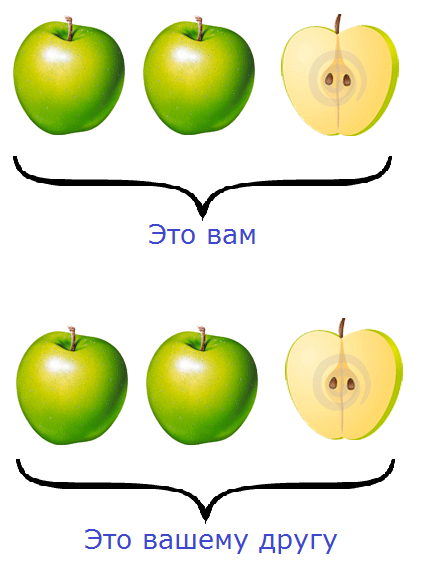
Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Теперь возвращаемся к дроби ![]() и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
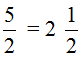
Схематически это выглядит так:
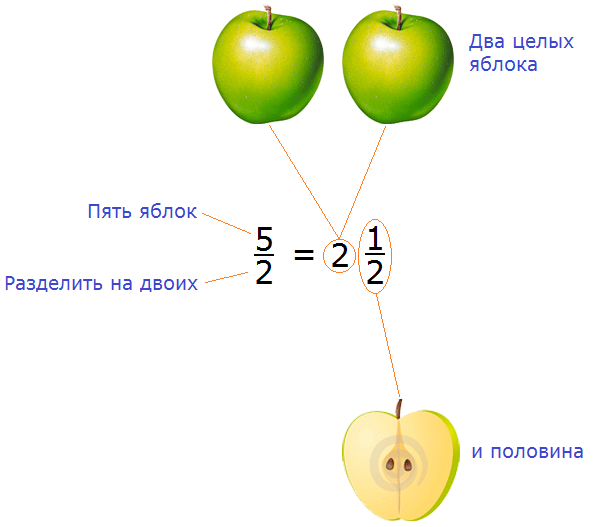
Процедуру, которую мы сейчас провели, называют выделением целой части дроби.
В нашем примере мы выделили целую часть дроби ![]() и получили новую дробь
и получили новую дробь ![]() . Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
. Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
В нашем примере целая часть это 2, а дробная часть это ![]()
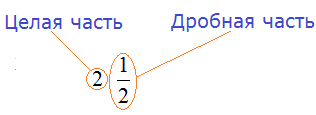
Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.
Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:
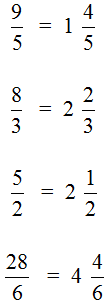
Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби ![]() . Записываем уголком данное выражение и решаем:
. Записываем уголком данное выражение и решаем:
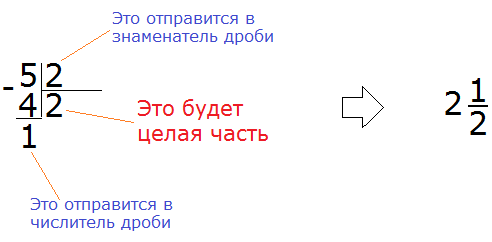
После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.
В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.
Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби ![]()
Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:

Получили: 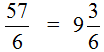
Перевод смешанного числа в неправильную дробь
Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь ![]() . Если выделить в ней целую часть, то получается
. Если выделить в ней целую часть, то получается ![]()
![]()
Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.
Например, переведём смешанное число ![]() в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
2 × 3 = 6
Затем к 6 прибавляем числитель дробной части:
6 + 1 = 7
Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:
![]()
Подробное решение выглядит так:
![]()
А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
![]()
Пример 2. Перевести смешанное число ![]() в неправильную дробь.
в неправильную дробь.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:
![]()
Основное свойство дроби
Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.
Например, рассмотрим дробь ![]() . Умножим её числитель и знаменатель на одно и то же число, например на число 2
. Умножим её числитель и знаменатель на одно и то же число, например на число 2
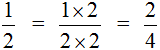
Получили новую дробь ![]() . Если верить основному свойству дроби, то дроби
. Если верить основному свойству дроби, то дроби ![]() и
и ![]() равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
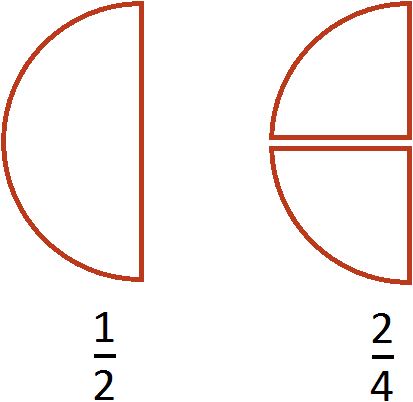
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь ![]() (один кусок из двух), а второй иллюстрирует дробь
(один кусок из двух), а второй иллюстрирует дробь ![]() (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
(два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями ![]() и
и ![]() можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
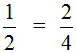
Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь ![]() . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
. Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
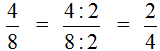
Получили новую дробь ![]() . Если верить основному свойству дроби, то дроби
. Если верить основному свойству дроби, то дроби ![]() и
и ![]() равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
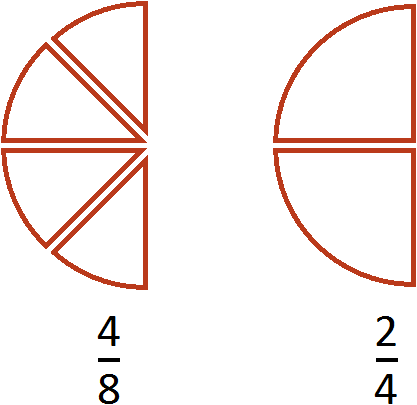
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь ![]() (четыре куска из восьми), а второй иллюстрирует дробь
(четыре куска из восьми), а второй иллюстрирует дробь ![]() (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
(два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями ![]() и
и ![]() можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
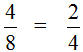
Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!
Сокращение дробей
Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь ![]() выглядит намного проще и красивее, чем дробь
выглядит намного проще и красивее, чем дробь ![]() .
.
Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.
Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.
Пример 1. Сократить дробь ![]()
Итак, нужно разделить числитель и знаменатель дроби ![]() на наибольший общий делитель чисел 2 и 4.
на наибольший общий делитель чисел 2 и 4.
В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби ![]() надо разделить на 2
надо разделить на 2
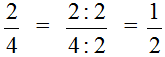
В результате дробь ![]() обратилась в более простую дробь
обратилась в более простую дробь ![]() . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.
. Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.
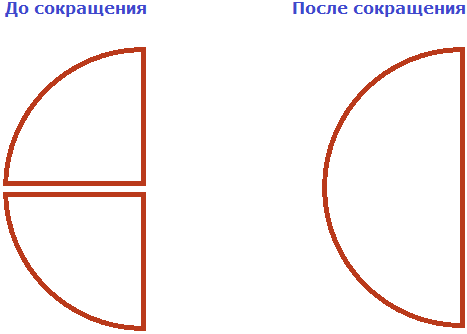
На рисунке представлены дроби ![]() и
и ![]() в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
Пример 2. Сократим дробь ![]()
Чтобы сократить дробь ![]() , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби ![]() на 20
на 20
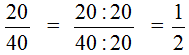
Пример 3. Сократим дробь ![]()
Чтобы сократить дробь ![]() , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби ![]() на 4
на 4
Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:
Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.
Второй способ сокращения дроби
Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.
К примеру, вернёмся к дроби ![]() . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
. Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
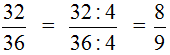
Теперь представьте, что в данном выражении отсутствует конструкция ![]() , и сразу записан ответ
, и сразу записан ответ ![]() . Получится следующее выражение:
. Получится следующее выражение:
![]()
Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.
Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:
![]()
Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:
![]()
Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36
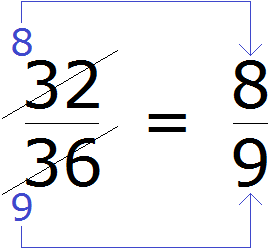
Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.
Например, сократим дробь ![]() , предварительно разложив на простые множители числитель и знаменатель:
, предварительно разложив на простые множители числитель и знаменатель:
![]()
Итак, мы разложили числитель и знаменатель дроби ![]() на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение: 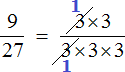
Сократить можно ещё по тройке в числителе и в знаменателе:
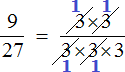
Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.
Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.
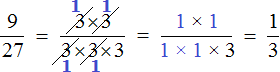
Получили ответ ![]() . Значит, при сокращении дроби
. Значит, при сокращении дроби ![]() получается новая дробь
получается новая дробь ![]() .
.
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.
Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:
![]()
Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:
Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?
Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
НОД и НОК
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения: ![]() и
и ![]()
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
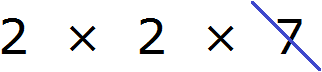
Теперь перемножаем оставшиеся множители и получаем НОД:
![]()
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
![]()
Перемножим оставшиеся числа:
![]()
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
 Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.
Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
![]()
Перемножим оставшиеся числа:
![]()
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
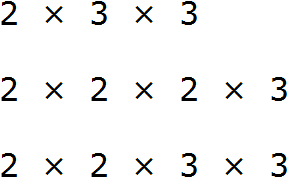
Теперь найдём и подчеркнём общие множители:
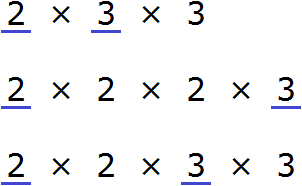
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12

Разложим на множители число 24
Разложим на множители число 36
Разложим на множители число 42
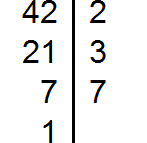
Получили четыре разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
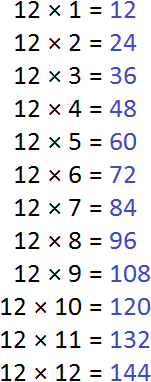
Теперь выпишем кратные обоих чисел:
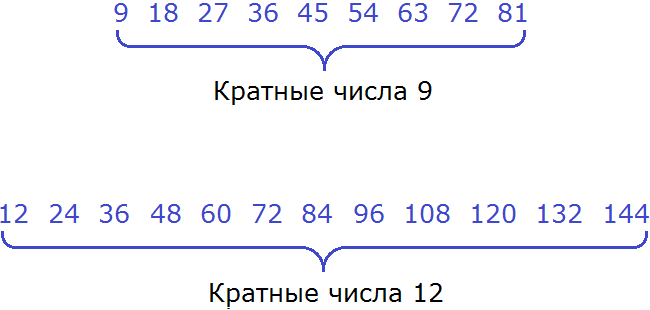
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
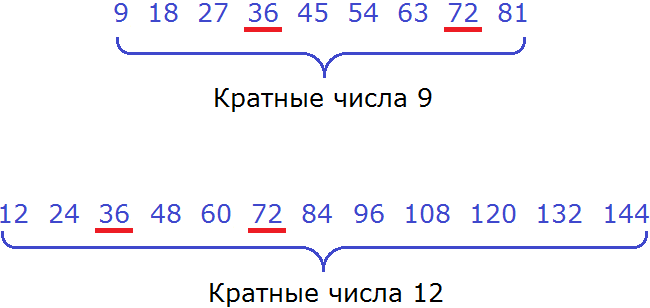
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Разложим на множители число 9
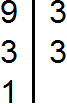
Разложим на множители число 12

Выпишем первое разложение:
![]()
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
![]()
Теперь перемножаем эти множители:
![]()
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
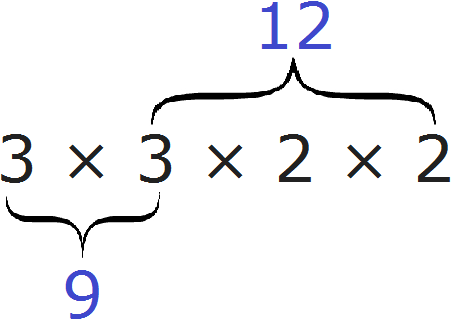
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
Разложим на множители число 180
Выпишем первое разложение:
![]()
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
![]()
Теперь перемножаем эти множители:
![]()
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
Разложим на множители число 15
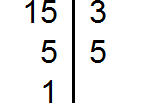
Разложим на множители число 33
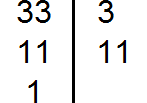
Выпишем первое разложение:
![]()
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
![]()
Теперь перемножаем эти множители:
![]()
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
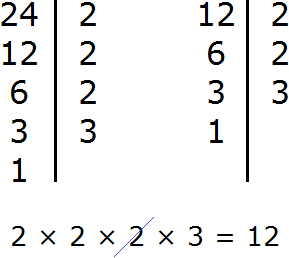
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
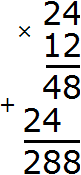
Разделим полученное число 288 на НОД чисел 24 и 12
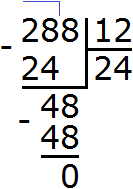
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
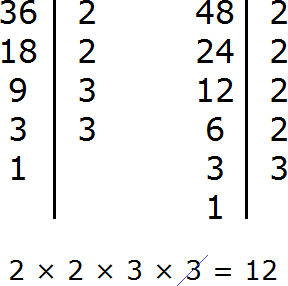
Перемножим числа 36 и 48
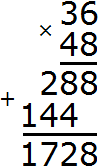
Разделим 1728 на НОД чисел 36 и 48
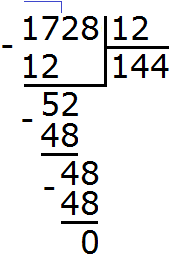
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
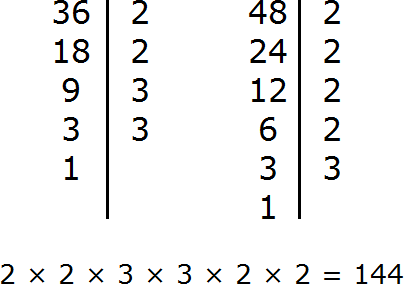
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Делители и кратные
В данном уроке мы рассмотрим такие понятия как делители и кратные.
Что такое делитель?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:
8 : 2 = 4
Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:
9 : 3 = 3
Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:
10 : 4 = 2 (2 в остатке)
Определение. Делителем числа а называется число, на которое число а делится без остатка.
Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 12 и прочитаем определение:
Делителем числа 12 называется число, на которое 12 делится без остатка.
Попробуем перечислить эти числа:
1, 2, 3, 4, 6, 12
Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Кратные числа
Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3
6 : 3 = 2
Определение. Кратным числа а называется число, которое делится без остатка на а.
Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 5 и прочитаем определение:
Кратным числа 5 называется число, которое делится без остатка на 5.
У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Примеры:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Примеры:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
27 : 3 = 9
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
18 : 9 = 2
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
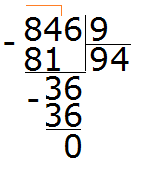
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
20 : 2 = 10
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
5 : 1 = 5
5 : 5 = 1
Значит, число 5 является простым числом.
Составным же называется число, которое имеет больше двух делителей. Например, число 4 составное, поскольку у него больше двух делителей: 4, 2 и 1
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
Значит, число 4 является составным числом.
Разложение составного числа на простые множители
Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.
Например, число 6 можно записать в виде суммы 4 + 2 или в виде частного 12 : 2 или в виде произведения 2 × 3. Последнюю запись 2 × 3 можно назвать разложением числа 6 на простые множители.
Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.
Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4
4 = 2 × 2
Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6
6 = 2 × 3
Разложим на множители число 8. Это число можно разложить на множители 2 и 4, при этом множитель 4 можно разложить на два множителя: 2 и 2. Поэтому вместо четвёрки записываем её разложение:
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10
180 = 18 × 10
Теперь раскладываем множители 18 и 10 на другие множители:
18 = 3 × 6
10 = 5 × 2
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:
6 = 2 × 3
Теперь собираем все простые множители вместе:
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.
Например, разложим предыдущее число 180 этим способом.
Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
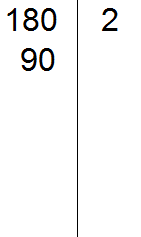
Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.
90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:
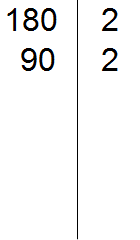
Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:
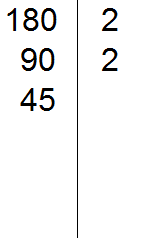
Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
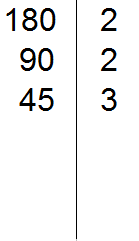
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
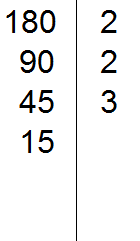
Теперь делим 15. Проверяем делится ли 15 на 2.
15 не делится на 2. Тогда проверяем делится ли 15 на 3.
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
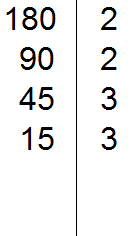
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:
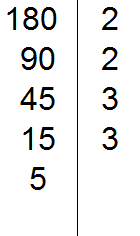
Теперь делим 5. Проверяем делится ли 5 на 2.
5 не делится на 2. Тогда проверяем делится ли 5 на 3.
5 не делится на 3. Тогда проверяем делится ли 5 на 5.
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:
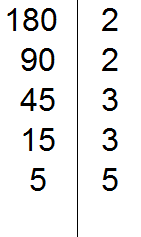
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:
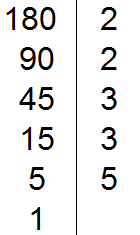
На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.
Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
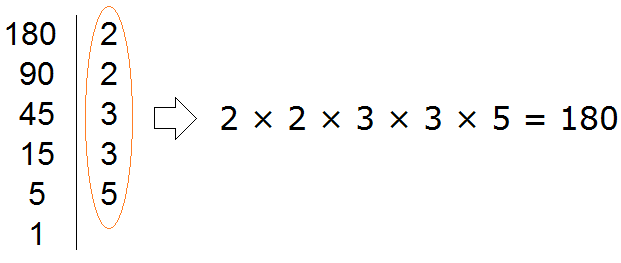
Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
Пример 1. Найти делители числа 12
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
2 × 2 = 4
Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
- записать в качестве первого делителя единицу;
- разложить исходное число на простые множители и выписать из полученных простых множителей те множители, которые являются делителями исходного числа (если множитель повторяется, то выписать его нужно только один раз);
- найти все возможные произведения полученных простых множителей между собой. Получаемые в результате ответы будут остальными делителями исходного числа.
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
1
Теперь разложим число 6 на простые множители:
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
Теперь найдём все возможные произведения простых множителей числа 6. В данном случае имеется только одно произведение, а именно 2 × 3. Это произведение равно 6. Допишем число 6 к нашим делителям:
1, 2, 3, 6
Таким образом, делителями числа 6 являются числа 1, 2, 3, 6.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Законы математики
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае — к тому что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
5 + 2 = 7
2 + 5 = 7
Если на одну чашу весов положить пакет, в котором 10 килограмм яблок, и на другую чашу так же положить пакет, в котором 10 килограмм яблок, то весы выровнятся, и не важно что яблоки в пакетах лежат вразброс.
Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
5 + 2 = 2 + 5
7 = 7
Полагаем что вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
a + b = b + a
Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
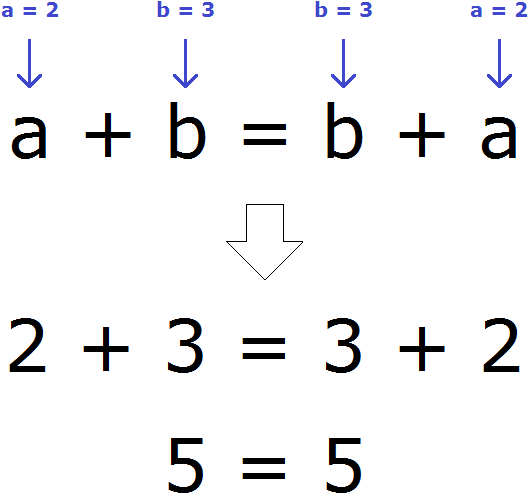
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
5 × 2 = 10
2 × 5 = 10
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
10 = 10
Запишем переместительный закон умножения с помощью переменных:
a × b = b × a
Для записи законов в качестве переменных необязательно использовать именно буквы a и b. Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
x × y = y × x
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
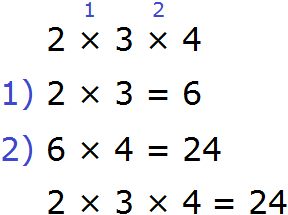
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
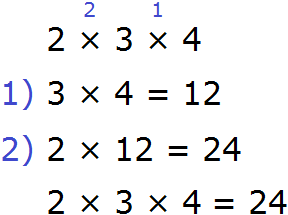
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
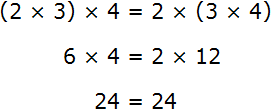
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
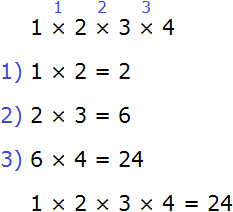
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
(3 + 5) × 2
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
(3 + 5) = 8
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
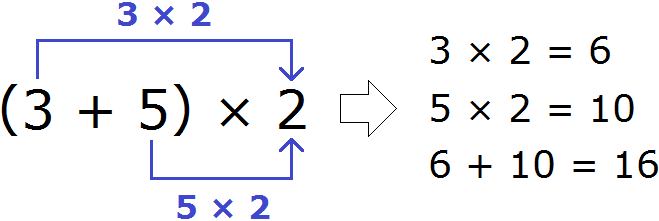
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
Или ещё короче:
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7
Задания для самостоятельного решения
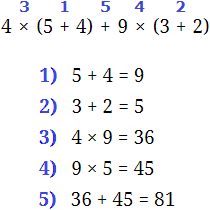
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Порядок действий
В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.
Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.
Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:
10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1
Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто как 2 + 2 или 9 − 3.
Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.
Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:
Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1
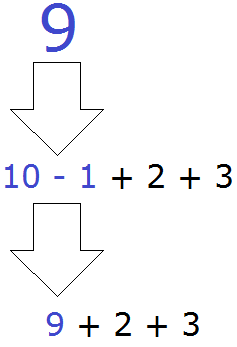
Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:
1. Сначала вычислить то, что находится в скобках!
2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!
3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!
Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:
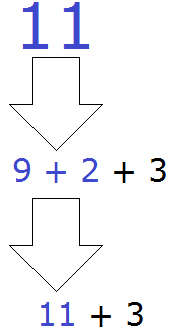
Осталось простейшее выражение 11 + 3, которое вычисляется легко:
11 + 3 = 14
Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14
10 − 1 + 2 + 3 = 14
Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:
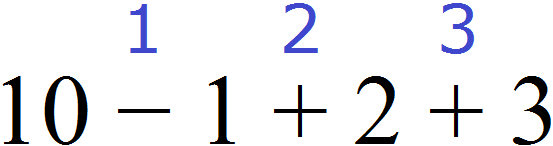
И далее можно выполнить действия по отдельности, что очень удобно:
1) 10 − 1 = 9
2) 9 + 2 = 11
3) 11 + 3 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:
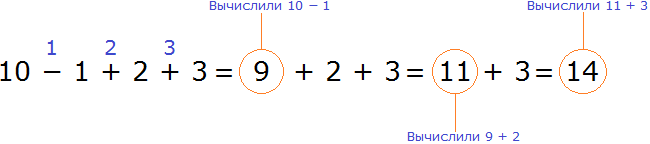
Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.
Пример 2. Найти значение выражения (3 + 5) + 2 × 3
Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:
8 + 2 × 3
Снова читаем первое правило:
Сначала вычислить то, что находится в скобках!
Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3
8 + 6
Осталось простейшее выражение 8 + 6, которое вычисляется легко:
8 + 6 = 14
Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14
(3 + 5) + 2 × 3 = 14
Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:
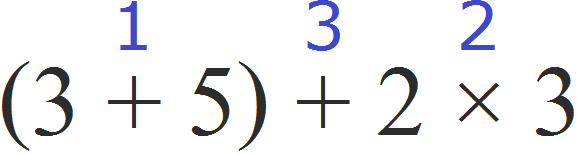
И далее можно выполнить действия по отдельности, что очень удобно:
1) 3 + 5 = 8
2) 2 × 3 = 6
3) 8 + 6 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
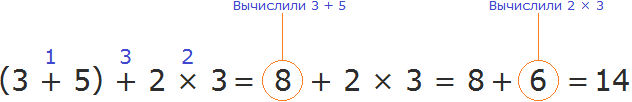
Но опять же, используя такой способ, нужно быть очень внимательным.
Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1
Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:
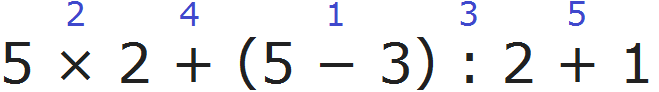
1) 5 − 3 = 2
2) 5 × 2 = 10
3) 2 : 2 = 1
4) 10 + 1 = 11
5) 11 + 1 = 12
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.
Пример 4. Найти значение выражения (3250 − 2905) : 5
Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым
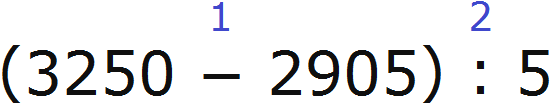
1) 3250 − 2905 = 345
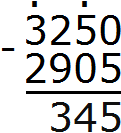
2) 345 : 5 = 69
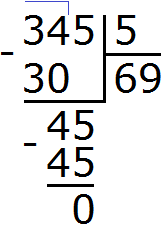
В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.
Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.
В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.
В результате будем иметь следующий порядок:
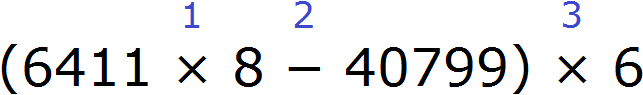
1) 6 411 × 8 = 51 288
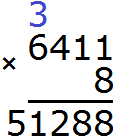
2) 51 288 − 40 799 = 10 489

3) 10 489 × 6 = 62 934
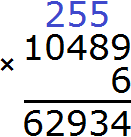
Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)
Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.
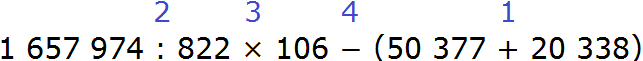
1) 50 377 + 20 338 = 70 715
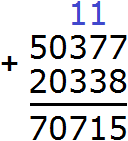
2) 1 657 974 : 822 = 2 017
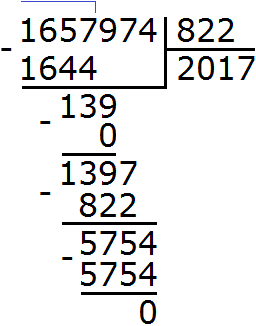
3) 2 017 × 106 = 213 802
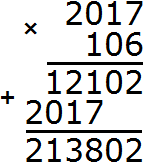
4) 213 802−70 715 = 143 087
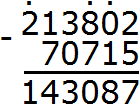
Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.
В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:
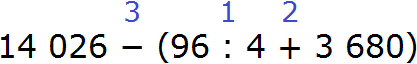
1) 96 : 4 = 24
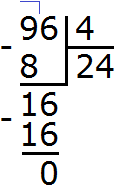
2) 24 + 3 680 = 3 704
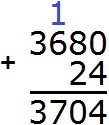
3) 14026 − 3 704 = 10 322
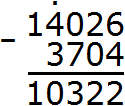
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Деление
Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.
Что такое деление?
Деление это действие, позволяющее что-либо разделить.
Деление состоит из трёх параметров: делимого, делителя и частного.
Делимое это то что делят;
Делитель это число, показывающее на сколько частей нужно разделить делимое.
Частное это собственно результат.
Пусть у нас имеются 4 яблока:

Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:
Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:
![]()
В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.
Говоря о делении, можно рассуждать и по-другому. Вернёмся к предыдущему выражению 4 : 2 = 2. Можно посмотреть на делитель 2 и задать вопрос «сколько двоек в четвёрке?» и ответить: «две двойки». Действительно, если сложить две двойки, то получится число 4
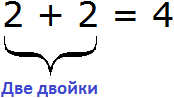
В ситуации с четырьмя яблоками можно задать вопрос «сколько раз два яблока содержатся в четырёх яблоках» и ответить: «два раза».

Чтобы научиться делить, нужно хорошо знать таблицу умножения. Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
![]()
Видно, что второе выражение записано в обратном порядке. Если у нас имеются два яблока и мы захотим увеличить их в пять раз, то запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то запишем 10 : 5 = 2
Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷
На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.
Деление с остатком
Остаток — это то что осталось от действия деления неразделённым.
Например, пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Можно проверить это умножением:
(2 × 2) + 1 = 5
Допустим, имеются пять яблок:

Разделим их поровну на двоих друзей. Но разделить поровну пять целых яблок не полýчится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:
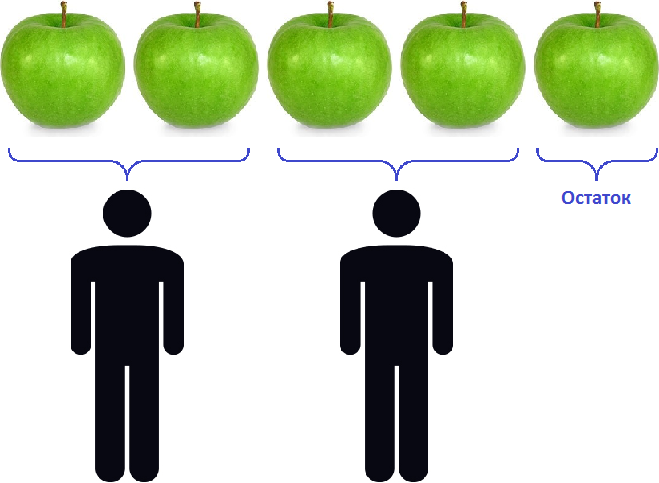
Деление уголком
Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.
Прежде чем делить уголком, человек должен знать:
- обычное деление маленьких чисел;
- деление с остатком;
- умножение в столбик;
- вычитание в столбик.
Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9 : 3. Уголком это выражение записывается следующим образом:
Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:
Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа: 3 × 3 = 9. Получили 9. Записываем эту девятку под делимым:
Теперь от делимого вычитаем девятку, которую мы под ним написали: 9 − 9 = 0. Остаток равен нулю. Проще говоря, остатка нет. На этом деление успешно завершено:
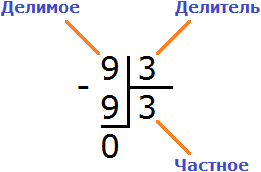
Пример 2. Найти значение выражения 8 : 3
Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.
Сначала запишем данное выражение уголком:
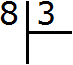
Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:
В школе частное подбирается методом подбора. Все мы слышали такие фразы как «берём по одному» , «берём по два» или «берём по три». У нас сейчас как раз такой случай. Мы взяли по два, ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:
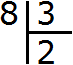
Теперь вынимаем остаток. Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:
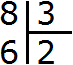
Далее из 8 вычитаем 6. Полученное число и будет остатком:
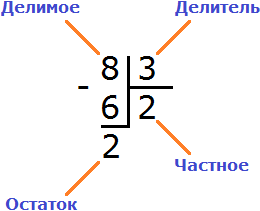
8 : 3 = 2 (2 в остатке)
Проверка:
(2 × 3) + 2 = 6 + 2 = 8
Деление многозначного числа на однозначное
Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.
В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.
Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.
Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя. Если больше, то её надо разделить на делитель, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то надо разделить их на делитель, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.
Сложно? Ни чуть, если мы разберём несколько примеров.
Пример 1. Найти значение выражения 25 : 3
25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше чем три? Да. Поэтому выполняем деление числа 25 на 3. Записываем уголком данное выражение и начинаем делить:
Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему. Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:
Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.
Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:

Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:
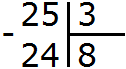 Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:
Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:
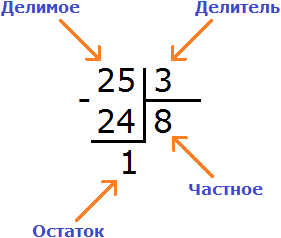
25 : 3 = 8 (1 в остатке)
Проверка:
(8 × 3) + 1 = 24 + 1 = 25
Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.
В приведённом примере последним остатком было число 1, а делителем число 3. Единица меньше чем три, поэтому деление завершено. Последний остаток мéньший делителя говорит о том, что он не содержит чисел равных делителю.
В нашем примере, если задать вопрос «сколько троек в единице?», то ответом будет «нисколько», потому что единица не содержит троек.
Пример 2. Разделить 326 на 4.
Смóтрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да. Значит можно выполнять деление.
Записываем уголком данное выражение:

Теперь задаём вопрос: «сколько четвёрок в числе 32?». В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:
Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:
 Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:
Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:
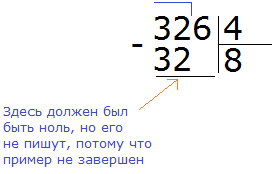 Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:
Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:
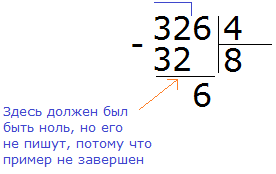
Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:
Записываем единицу в правом уголке нашего ответа:
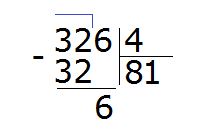 Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:
Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:
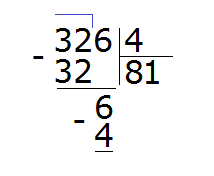
Затем из 6 вычитаем 4, получаем число 2, которое является остатком:
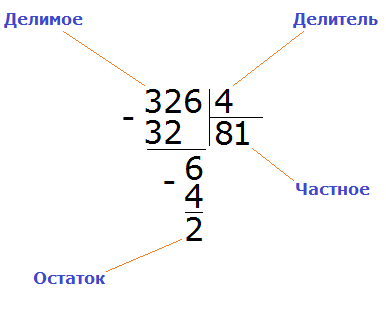
Получили 326 : 4 = 81 (2 в остатке)
Проверка: (81 × 4) + 2 = 324 + 2 = 326
Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.
Вернёмся к предыдущему примеру 326 : 4. Первое неполное делимое в данном выражении было число 32, поскольку его мы разделили в первую очередь.
А в примере 25 : 3 первое неполное делимое было 25.
Пример 3. Найти значение выражения 384 : 5
Записываем данное выражение в уголком:
Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:
Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:
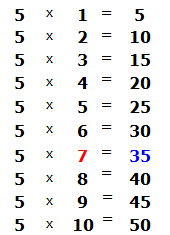
Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение. Это множитель 7, который выделен красным.
Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:
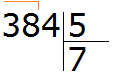 Умножаем 7 на 5, получаем 35 и записываем его под 38:
Умножаем 7 на 5, получаем 35 и записываем его под 38:
Теперь из 38 вычитаем 35, получим 3:
Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:
Видно, что после того, как мы снесли четвёрку, она вместе с тройкой образовала число 34. Это число 34 мы будем делить на 5. Для этого опять задаем вопрос: «сколько пятёрок в числе 34?». Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему или равно ему:
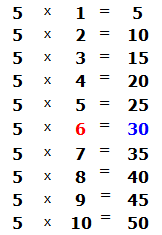
Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:
Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:
Теперь из 34 вычитаем 30, получаем 4. Эта четвёрка будет остатком от деления 384 на 5
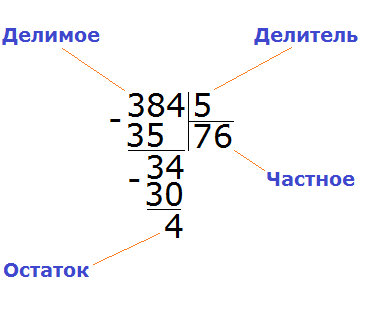
384 : 5 = 76 (и 4 в остатке)
Проверка:
(76 × 5) + 4 = 380 + 4 = 384
Пример 4. Найти значение выражения 8642 : 4
Этот пример немного посложнее. Записываем уголком данное выражение:
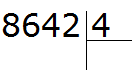
Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2
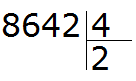 Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:
Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:
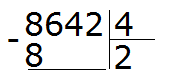
Вытаскиваем остаток: 8 − 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не записываем, поскольку решение примера не завершено.
Далее сносим цифру 6 и делим её на делитель, получаем 1
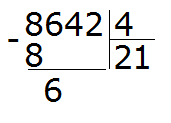 Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:
Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:
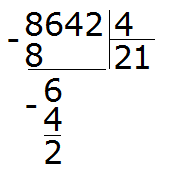
Получили остаток 2. Это остаток, который остался от деления 6 на 4.
Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6
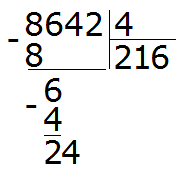
Умножаем 6 на 4, получаем 24. Записываем это число под 24
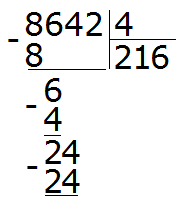
Вытаскиваем остаток: 24 − 24 = 0. Ноль это остаток от деления 24 на 4. Ноль, как мы уже договорились, не записываем. Далее сносим последнюю цифру 2
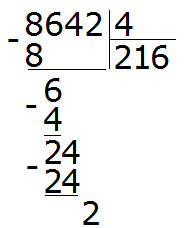
Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Если мы зададим вопрос «сколько четвёрок в двойке?«, то ответом будет ноль, поскольку двойка меньше четвёрки и не может содержать в себе число, бóльшее себя самогó.
Поэтому два разделить на четыре это ноль:
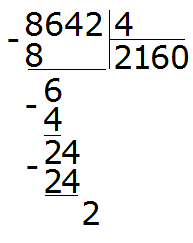 Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:
Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:
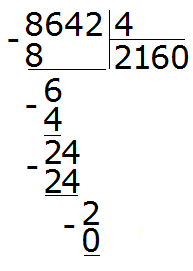
Теперь находим остаток: 2 − 0 = 2. Двойка это остаток от деления 8642 на 4. Таким образом, пример завершён:
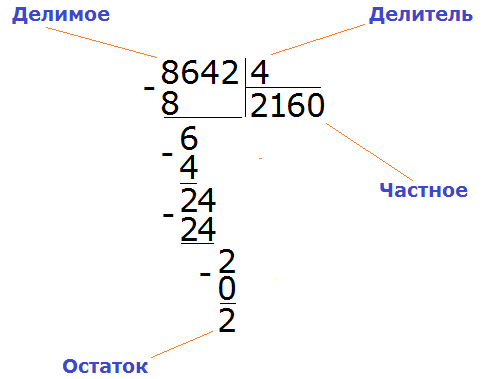
8642 : 4 = 2160 (2 в остатке)
Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642
Деление чисел, у которых на конце 0
Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.
Например, разделим 120 : 3
Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:
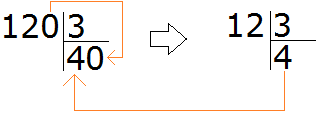
Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее находим остаток: 120 − 120 = 0. Остаток равен нулю. Пример завершён.
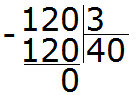
120 : 3 = 40
Проверка 40 × 3 = 120.
Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:
12 : 3 = 4 (делимое без нулей на конце)
120 : 3 = 40 (здесь у делимого один ноль)
1200 : 3 = 400 (здесь у делимого два нуля)
12000 : 3 = 4000 (здесь у делимого три нуля)
В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.
Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5
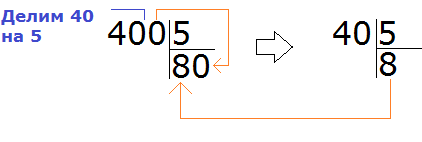 Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:
Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:
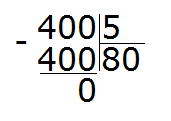 Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.
Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:
1000 + 400 = 1400
Можно по-отдельности разделить 1000 на 5 и 400 на 5:
1000 : 5 = 200
400 : 5 = 80
и сложить полученные результаты:
200 + 80 = 280
Итого: 1400 : 5 = 280
Решим этот же пример уголком:
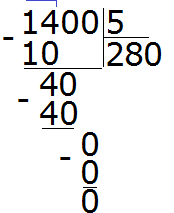
Деление многозначного числа на многозначное
Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так-то просто.
Принцип деления остаётся тем же что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.
Для начала введём новое понятие — круглое число. Круглым будем называть число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 500, 600, 1000, 13000
Любое число можно превратить в круглое. Для этого первую цифру, образующую самый старший разряд, оставляют без изменений, а остальные цифры заменяют нулями.
Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10
Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.
Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.
Превратим число 13735 в круглое число. Первая цифра 1 образуют старший разряд (разряд десятков тысяч) — эту цифру оставляем без изменений, а остальные цифры заменяем нулями. В итоге получаем 10000.
Внимание! В дальнейшем понятия круглого числа и перевод любого числа в круглое будут рассмотрены более подробно.
Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное надо находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.
Пример 1. Найти значение выражения 88 : 12
Записываем данное выражение уголком:
 Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.
Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.
Со школы мы помним, что частное подбиралось методом угадывания, говоря «берем по два» или «берем по три».
Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число которое меньше делимого, но очень близко к нему или равно ему.
Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12
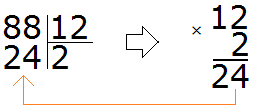
Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит.
Пробуем следующее число. Допустим частное равно 5
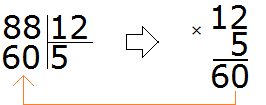
Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит.
Попробуем сразу взять по 8
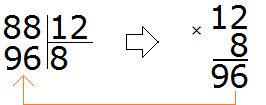
На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7
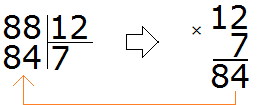
Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.
88 : 12 = 7 (4 в остатке)
Проверка: (12 × 7) + 4 = 84 + 4 = 88
Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.
Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.
Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.
Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.
В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.
Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:
800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)
800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)
900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)
400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)
320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)
Заметно, что всё в конечном итоге свóдится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.
Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания.
Для начала превращаем делимое и делитель в круглые числа.
Круглым числом для 88 будет число 80.
А круглым числом для 12 будет число 10.
Теперь делим полученные круглые числа:
 80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:
80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:
Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.
Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.
Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:

Как видно, этим способом мы решили этот пример намного быстрее.
Пример 2. Найти значение выражения 1296 : 144
Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:
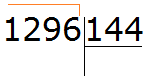 Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.
Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.
Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.
Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144
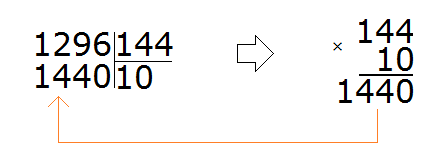
Десятка не подходит, поскольку при умножении получается число, которое больше делимого.
Попробуем взять по 9, уменьшив десятку на единицу.
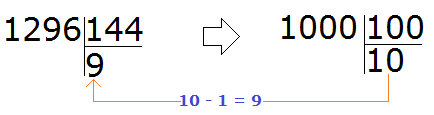
Проверяем девятку. Для этого умножаем её на делитель:
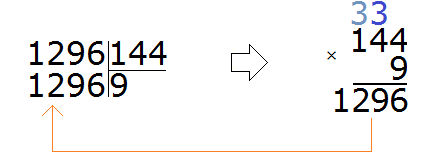
Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296
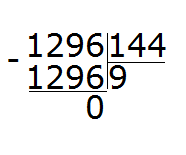 1296 : 144 = 9
1296 : 144 = 9
Проверка: 144 × 9 = 1296
Пример 3. Попробуем решить большой и сложный пример 227 492 : 331
Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.
Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300
 Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:
Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:
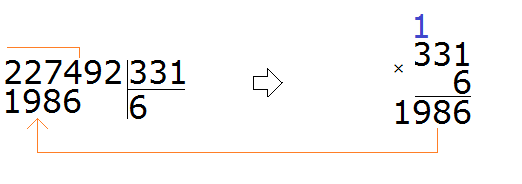 Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:
Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:
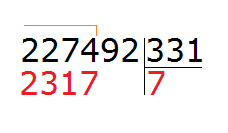 Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.
Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.
Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:
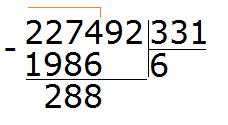
288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:
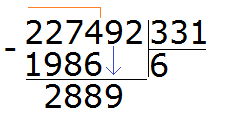
Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:
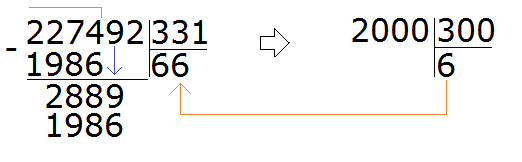 Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:
Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:
 Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:
Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:

Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.
Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241
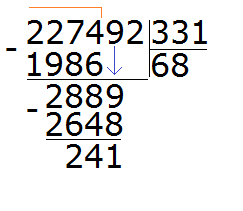
241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:
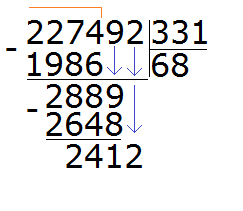
Теперь делим 2412 на 331. Возьмём по 7
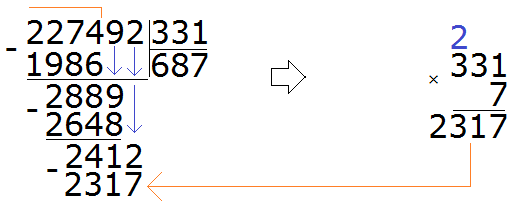
Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:

227 492 : 331 = 687 (95 в остатке)
Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492
На этом данный урок можно завершить. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.
Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Умножение
В этом уроке мы изучим умножение чисел. Напомним, что для умножения маленьких чисел предназначена таблица умножения. Обязательно выучите её наизусть, поскольку любое умножение больших чисел в конечном итоге свóдится к тому, чтобы умножить маленькие.
Однозначные и многозначные числа
Для начала введём два новых понятия: однознáчные и многознáчные числа.
Однознáчным называется число, которое состоит из одной цифры. Например, следующие числа являются однознáчными:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Слово «однознáчные» говорит само за себя. Однознáчное — значит состоит из одного знака (цифру иногда называют знáком).
Многознáчным называется число, которое состоит из двух и более цифр. Например, следующие цифры являются многознáчными:
10, 11, 15, 255, 350, 1000, 12500
Многознáчных чисел бесконечно много. Их не сосчитать. Кроме того, они подразделяются на следующие виды:
- двузнáчные, которые состоят из двух цифр (например, 25);
- трёхзнáчные, которые состоят из трёх цифр (например, 563);
- четырёхзнáчные, которые состоят из четырёх цифр (например, 1400)
и так далее, в зависимости от того сколько цифр в числе.
Умножение однозначных чисел
Однозначные числа умножаются легко. Достаточно знать таблицу умножения. Примеры:
5 × 5 = 25
3 × 5 = 15
7 × 6 = 42
5 × 8 = 40
Если по каким-либо причинам не удаётся вспомнить таблицу умножения, то можно воспользоваться сложением. Ведь умножение это ни что иное как многократное сложение.
Чтобы умножить, например, число 4 на число 3, нужно число 4 сложить три раза:
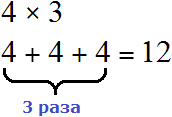
Умножение на 10, 100, 1000
Чтобы умножить любое число на 10, 100 или 1000, достаточно дописáть к множимому количество нулей из множителя.
Например, чтобы умножить 12 на 10, нужно к множимому 12 дописать в конце ноль из множителя 10. В результате получим ответ 120
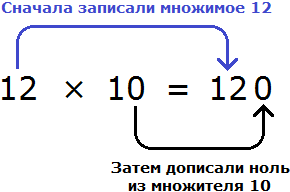
Еще примеры:
12 × 100 = 1200 (к 12 дописали два нуля, поскольку в числе 100 два нуля)
12 × 1000 = 12000 (к 12 дописали три нуля, поскольку в числе 1000 три нуля)
15 × 100 = 1500 (к 15 дописали два нуля, поскольку в числе 100 два нуля)
320 × 100 = 32000 (к 320 дописали два нуля, поскольку в 100 два нуля)
Если нулём оканчивается не множитель, а множимое, то для получения ответа нужно дописать ноль после множителя.
Например, чтобы умножить 10 на 12, нужно в ответе записать множитель 12 и дописать в конце один ноль:
10 × 12 = 120
Умножение чисел, которые оканчиваются нулями
Если оба числа оканчиваются нулями, то нужно перемнóжить те цифры, которые нулями не являются, затем к полученному результату дописáть все нули из обоих чисел.
Например, умнóжим 20 на 30.
20 × 30
Видим, что оба числá содержат по нулю. Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 2 и 3. Два умножить на три будет шесть:
20 × 30 = 6
Теперь к полученному результату, то есть к числу 6 дописываем все нули из обоих чисел. В числе 20 один ноль, в числе 30 также один ноль. Итого два нуля. Дописываем два нуля к числу 6
20 × 30 = 600
Пример 2. Умножить 40 на 300
Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 4 и 3. Четыре умножить на три будет двенадцать:
40 × 300 = 12
Теперь к полученному результату, то есть к числу 12 дописываем все нули из обоих чисел. В числе 40 один ноль, в числе 300 — два нуля. Итого три нуля. Дописываем три нуля к числу 12
40 × 300 = 12000
Пример 3. Умножить 600 на 3000
Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 6 и 3. Шесть умножить на три будет восемнадцать:
600 × 3000 = 18
Теперь к полученному результату, то есть к числу 18 дописываем все нули из обоих чисел. В числе 600 два нуля, в числе 3000 — три нуля. Итого пять нулей. Дописываем пять нулей к числу 18
600 × 3000 = 1800000
Умножение многозначного числа на однозначное
Чтобы умножить многозначное число на однозначное, надо умножить каждую цифру многозначного числа на это однозначное число. Например, найдем значение выражения 12 × 3. Записываем данное выражение в столбик, при этом единицы должны быть под единицами. Всё это соединяется знаком умножения ( × )
Далее каждая цифра многозначного числа умножается на 3. Умножать начинаем с разряда единиц, то есть с цифры 2. Два умножить на три будет шесть. Записываем цифру 6 в разряде единиц нашего ответа:
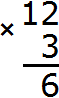
Теперь умножаем 1 на 3, получаем 3. Записываем цифру 3 в разряде десятков нашего ответа:
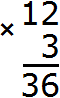
Получили ответ 36.
В данном примере множимым было число 12, а множителем число 3. Число 12 это две единицы и один десяток. Наша задача заключалась в том, чтобы увеличить эти две единицы и один десяток в 3 раза. Тогда решая этот пример, можно было бы рассуждать следующим образом:
Увеличим две единицы в 3 раза: 2 × 3 = 6. Получили шесть единиц. Записываем цифру 6 в разряде единиц нового числа
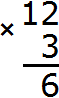
Увеличим один десяток в 3 раза: 1 × 3 = 3. Получили три десятка. Записываем цифру 3 в разряде десятков нового числа:
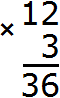
Иногда при умножении одной цифры многозначного числа на однозначное число получается многозначное число. В этом случае сначала записывается одна цифра из разряда единиц, а остальные цифры переносятся на следующий разряд, к которому они будут добавлены после вычисления.
Например, найдем значение выражения 23 × 6
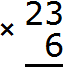
Умножаем каждую цифру числа 23 на 6. Начинаем с тройки: 3 × 6 = 18. Восемнадцать не вмещается в разряд единиц нашего ответа, поэтому сначала записывается 8, а 1 переносится на следующий разряд. Эта единица будет прибавлена к результату умножения 2 на 6
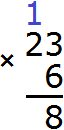
Теперь умножаем 2 на 6, получаем 12, плюс единица, которая досталась от предыдущего умножения. На рисунке эта единица выделена синим цветом. Вычисляем (2 × 6) + 1 = 13
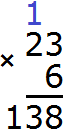
Получили ответ 138. В данном примере множимым было число 23, а множителем число 6. Число 23 это три единицы и два десятка. Наша задача заключалась в том, чтобы увеличить эти три единицы и два десятка в 6 раз. Тогда решая этот пример, можно было бы рассуждать следующим образом:
Увеличим три единицы в 6 раз: 3 × 6 = 18. Получили восемнадцать единиц. Произошло переполнение разряда в разряде единиц. Число 18 это 8 единиц и 1 десяток. 8 единиц записываем в разряде единиц нового числа, а 1 десяток отправляем к разряду десятков. Этот десяток мы прибавим, когда увеличим два десятка в шесть раз:
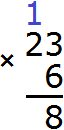
Увеличим два десятка в 6 раз: 2 × 6 = 12. Получили двенадцать десятков. Плюс прибавляем один десяток, который остался от числа 18.
12 десятков плюс 1 десяток будет 13 десятков. Записываем число 13 в разряде десятков нового числа, образуя окончательный ответ:
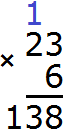
Пример 3. Найти значение выражения 326 × 5
Записываем в столбик данное выражение:
Умножаем каждую цифру числа 326 на 5. Начинаем с шестёрки: 6 × 5 = 30. Число 30 не вмещается в разряд единиц нашего ответа, поэтому сначала записываем 0, а тройку переносим на следующий разряд:
Теперь умножаем 2 на 5, получаем 10 плюс тройка, которая досталась от предыдущей операции: (2 × 5) + 3 = 13. Получили число 13, которое не вмещается в разряд десятков нашего ответа. Поэтому записываем сначала 3, а единицу переносим на следующий разряд:
Теперь умножаем последнюю тройку на 5, плюс прибавляем единицу, которая досталась от предыдущей операции: (3 × 5) + 1 = 16. Получили 16. Записываем это число целиком, образуя окончательный ответ:
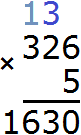
Умножение многозначных чисел на многозначные
Умножение многозначных чисел на многозначные происходит таким же образом, как и умножение многозначных на однозначные. Каждая цифра многозначного числа умножается на каждую цифру другого многозначного числа. Единственное отличие заключается в том, что в конце образуется своего рода лесенка ответов, которые надо сложить. Рассмотрим несколько примеров, чтобы хорошо понять это.
Пример 1. Найти значение выражения 12 × 14
Записываем данное выражение в столбик — единицы под единицами, десятки десятками:
Теперь умножаем каждую цифру числа 12 на каждую цифру числа 14. Делать это надо по-очереди, начав с четвёрки. В результате таких действий мы приходим к умножению многозначного числа на однозначное, которое проходили ранее:
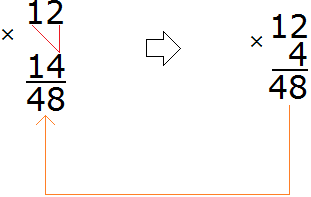
Умножив 12 на 4, мы получили число 48, которое записали таким образом, чтобы разряд единиц этого числа оказался под четверкой, на которую мы умножали число 12.
Теперь умножаем 12 на 1:
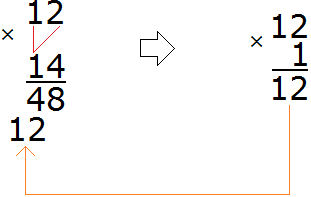
Умножив 12 на 1 мы получили число 12 и записали его таким образом, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножали число 12.
Мы получили лесенку ответов 48 и 12, которую надо сложить. Складываем и получаем ответ 168
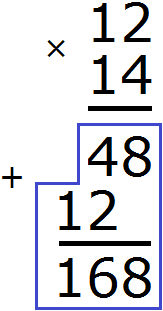
В данном примере множитель 14 это четыре единицы и один десяток. Тогда умножение 12 на 14 можно понимать как увеличение числа 12 в четыре раза и в десять раз. Этим и объясняется появление лесенки в конце решения. Давайте посмотрим как это выглядит на каждом этапе:
Увеличим число 12 в четыре раза, получим число 48
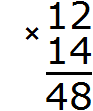
Увеличим число 12 в десять раз, получим число 120. Записываем 120 так, чтобы можно было сложить единицы этого числа с единицами числа 48, а десятки числа 120 можно было сложить с десятками числа 48
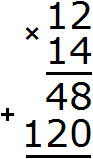
Теперь сложим получившуюся лесенку ответов. Единицы сложим с единицами, десятки с десятками, сотни с сотнями. В результате образуется окончательный ответ:

Но чаще всего множитель не группируется с помощью разрядов, и умножение выполняют, умножая каждую цифру множимого на каждую цифру множителя.
Пример 2. Найти значение выражения 25 × 36
Записываем данное выражение в столбик
Умножаем каждую цифру числа 25 на каждую цифру числа 36.
Умножим 25 на 6:
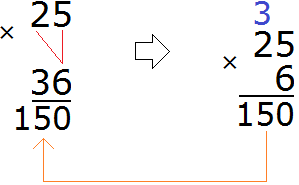
Умножаем 25 на 3:
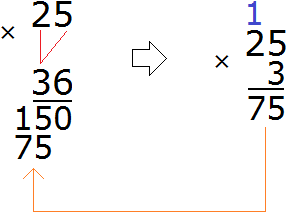
Теперь сложим получившуюся лесенку:
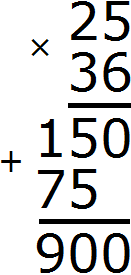
Получили ответ 900.
Рассмотрим большой и сложный пример на умножение: 12305 × 5641. Будем придерживаться ранее изученных правил.
Сначала записываем в столбик данное выражение
 Теперь начинаем умножать. Число 12305 надо умножить на каждую цифру числа 5641.
Теперь начинаем умножать. Число 12305 надо умножить на каждую цифру числа 5641.
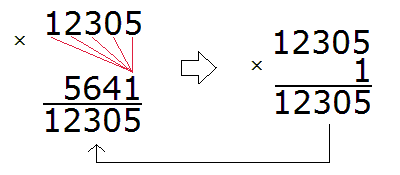
Умножив 12305 на 1, мы получили 12305 и записали это число так, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножили 12305.
Теперь умножаем 12305 на следующую цифру 4:
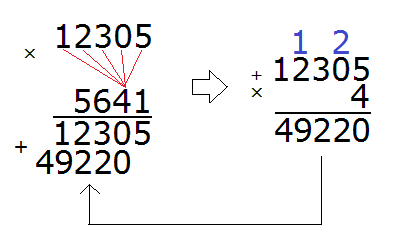 Умножив 12305 на 4, мы получили 49220 и записали это число так, чтобы разряд единиц этого числа оказался под четверкой, на которую умножали 12305.
Умножив 12305 на 4, мы получили 49220 и записали это число так, чтобы разряд единиц этого числа оказался под четверкой, на которую умножали 12305.
Умножаем 12305 на следующую цифру 6:
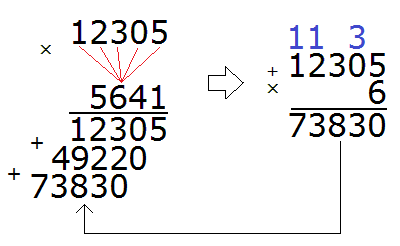
Умножив 12305 на 6, мы получили 73830 и записали это число так, чтобы разряд единиц этого числа оказался под шестёркой, на которую мы умножали 12305.
Теперь умножаем 12305 на последнюю цифру 5:

Умножив 12305 на 5, мы получили 61525 и записали это число так, чтобы разряд единиц этого числа оказался под пятёркой, на которую умножали 12305.
В результате мы получили большую лесенку, которую надо сложить. Складываем:
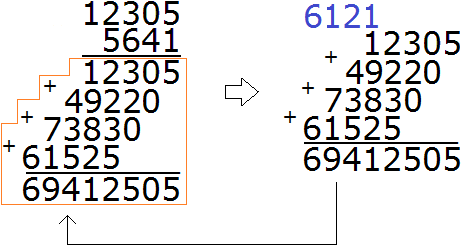
Получили окончательный ответ 69412505.
Если вы поняли этот пример, то можно сказать, что умножение больших чисел вы усвоили на отлично.
На этом урок по умножению можно завершить. Обязательно потренируйтесь, решив несколько примеров, которые даны ниже.
Важно отметить, что все эти стрелки и подробные решения, как на картинках в «боевых условиях» рисовать не принято. Нужно уметь сразу записывать ответы, выполняя в уме все вычисления.
Исключением является то, если человек давно не занимался математикой или никогда ею не занимался. В таком случае можно рисовать для себя стрелки и другие вспомогательные схемы для хорошего усвоения материала.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже