Квадратный корень легко извлекается с помощью калькулятора. Для этого достаточно набрать на нём исходное число и нажать клавишу корня ![]()
Если калькулятора под рукой нет, то квадратный корень извлекают пользуясь алгоритмом извлечения квадратного корня.
Применение алгоритма может оказаться весьма полезным на контрольных и экзаменах. Ведь чаще всего на таких мероприятиях использовать калькулятор запрещено.
Как пользоваться алгоритмом
Рассмотрим применение алгоритма извлечения квадратного корня на конкретных примерах. О том, почему алгоритм следует применять именно так, поговорим позже.
Пример 1. Извлечём квадратный корень из числа 4096 с помощью алгоритма извлечения квадратного корня.
Прежде всего сгруппируем число 4096 по две цифры. Двигаясь с конца влево сделаем небольшую мéтку:
![]()
Сгруппированные цифры исходного числа называют грáнями, а саму группировку по две цифры разделением на грáни. Количество грáней позволяет предположить сколько цифр будет содержаться в извлечённом корне. В нашем примере извлечённый корень будет содержать две цифры, поскольку исходное число содержит две грани.
Теперь нужно извлечь квадратный корень из числа 40 с точностью до целых, получаем 6. Записываем 6 после знака равенства:
![]()
Далее возвóдим число 6 в квадрат и полученный результат записываем под числом 40
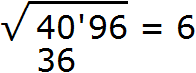
Далее вычитаем из числа 40 число 36, получаем 4. Записываем это число под 36
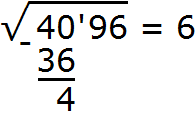
Снóсим оставшиеся цифры из под корня, а именно 96. Получаем остаток 496
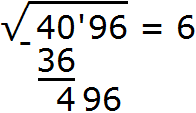
Теперь нужно найти следующую цифру корня. Её находят так. Первую найденную цифру корня, а именно 6 умножаем на 2, получаем 12. К числу 12 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 496 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 5. Допишем её к числу 12 и умножим образовавшееся число 125 на 5
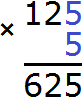
Получилось число 625, которое больше остатка 496. Значит цифра 5 не годится в качестве следующей цифры корня. Проверим тогда цифру 4. Допишем ее к числу 12 и умножим образовавшееся число 124 на 4
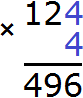
Получилось число 496, которое в точности является нашим остатком. Значит дописанная к числу 12 цифра 4 является следующей цифрой корня. Возвращаемся к исходному примеру и записываем цифру 4 в ответе после цифры 6
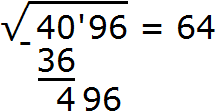
А число 496, которое получилось в результате умножения 124 на 4 записываем под остатком 496
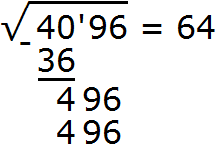
Выполняем вычитание 496 − 496 = 0. Ноль в остатке говорит о том, что решение окончено:
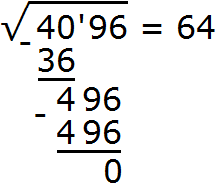
Для удобства поиска второй цифры, слева от остатка проводят вертикáльную линию и уже за этой линией записывают умножение. В нашем случае умножение 124 на 4. Результат умножение сразу записывают под остатком:
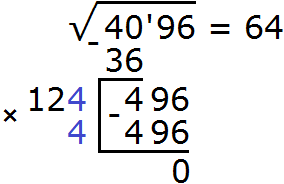
Итак, квадратный корень из числа 4096 равен 64
![]()
Пример 2. Извлечём квадрáтный корень из числа 441 с помощью алгоритма извлечения квадратного корня.
Прежде всего сгруппируем число 441 по две цифры. Двигаясь с конца влево сделаем небольшую мéтку. В данном случае в числе 441 только три цифры. Поэтому группируем цифры 4 и 1. Крайняя четвёрка слева будет сама по себе:
![]()
Теперь нужно извлечь квадратный корень из числа 4 с точностью до целых, получаем 2. Записываем 2 после знака равенства:
![]()
Далее возвóдим число 2 в квадрат и полученный результат записываем под числом 4
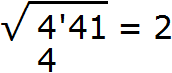
Вычитаем из числа 4 число 4, получаем 0. Ноль принято не записывать. Снóсим оставшиеся цифры корня, а именно 41
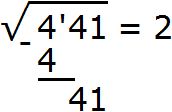
Теперь нахóдим следующую цифру корня. Первую найденную цифру корня, а именно 2 умножаем на 2, получаем 4. К числу 4 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить получившееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 41 или хотя бы максимально близким ему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 4 и умножим получившееся число 42 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 41
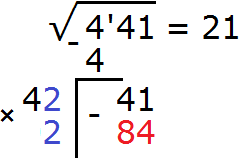
Получилось число 84, которое больше остатка 41. Значит цифра 2 не годится в качестве следующей цифры корня. Проверим тогда цифру 1. Допишем ее к числу 4 и умножим получившееся число 41 на на ту же самую дописанную цифру 1
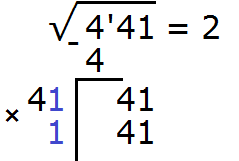
Получилось число 41, которое в точности является нашим остатком. Значит дописанная к числу 4 цифра 1 является следующей цифрой корня. Записываем цифру 1 после цифры 2
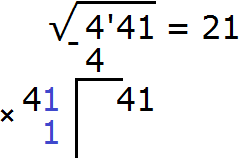
А число 41, которое получилось в результате умножения 41 на 1, записываем под остатком 41
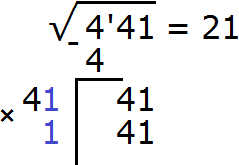
Выполняем вычитание 41 − 41 = 0. Ноль в остатке говорит о том, что решение окончено:
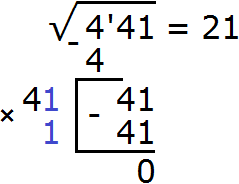
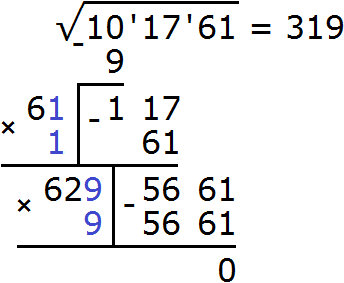
Пример 3. Извлечём квадратный корень из числа 101761 с помощью алгоритма извлечения квадратного корня.
Разбиваем число 101761 на грани:
![]()
Получилось три грани. Значит корень будет состоять из трёх цифр.
Извлекáем квадратный корень из первой грани (из числа 10) с точностью до целых, получаем 3. Записываем 3 после знака равенства:
![]()
Далее возвóдим число 3 в квадрат и полученный результат записываем под первой гранью (под числом 10)
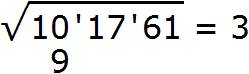
Вычитаем из числа 10 число 9, получаем 1. Снóсим следующую грань, а именно число 17. Получаем остаток 117
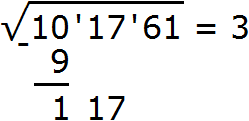
Теперь нахóдим вторую цифру корня. Первую найденную цифру корня, а именно 3 умножаем на 2, получаем 6. К числу 6 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 117 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 6 и умножим образовавшееся число 62 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 117
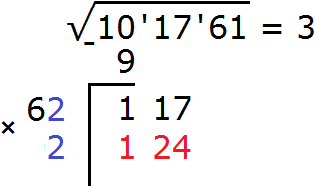
Получилось число 124, которое больше остатка 117. Значит цифра 2 не годится в качестве второй цифры корня. Проверим тогда цифру 1. Допишем ее к числу 6 и умножим образовавшееся число 61 на на ту же самую дописанную цифру 1
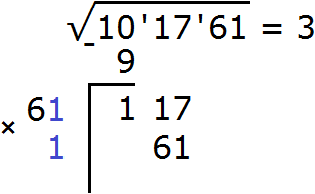
Получилось число 61, которое не превосходит остатка 117. Значит дописанная к числу 6 цифра 1 является второй цифрой корня. Записываем её в ответе после цифры 3
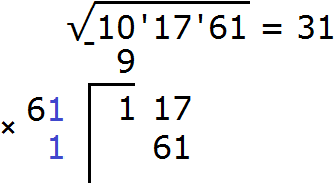
Теперь выполняем вычитание 117 − 61 = 56.
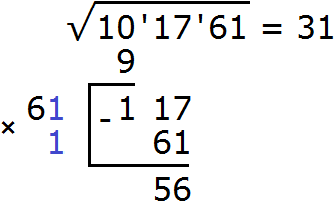
Снóсим следующую грань, а именно число 61. Получаем новый остаток 5661
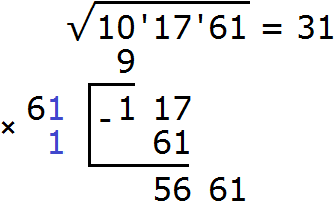
Теперь нахóдим третью цифру корня. Первые две найденные цифры корня, а именно число 31 умножаем на 2, получаем 62. К числу 62 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет третьей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 5661 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 9. Допишем её к числу 62 и умножим образовавшееся число 629 на ту же самую дописанную цифру 9. Результат умножения будем записывать сразу под остатком 5661
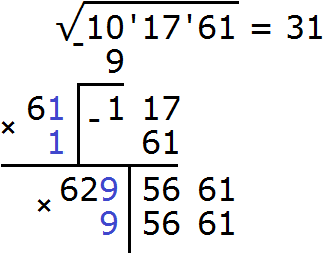
Получилось число 5661, которое в точности является нашим остатком. Значит дописанная к числу 62 цифра 9 является третьей цифрой корня. Записываем цифру 9 в ответе после цифры 1

Выполняем вычитание 5661 − 5661 = 0. Ноль в остатке говорит о том, что решение окончено:
Пример 4. Извлечём квадратный корень из числа 30,25 с помощью алгоритма извлечения квадратного корня.
Данное число является десятичной дробью. В данном случае на грани следует разбить целую и дробную часть. Целую часть на грани следует разбить, двигаясь влево от запятой. А дробную — двигаясь вправо от запятой:
![]()
Получилось по одной грани в каждой части. Это значит, что корень будет состоять из двух цифр: одна цифра будет в целой части корня и одна цифра в дробной.
Извлечём квадратный корень из первой грани (из числа 30) с точностью до целых, получаем 5. Записываем 5 после знака равенства:
![]()
Далее возвóдим число 5 в квадрат и полученный результат записываем под первой гранью (под числом 30)
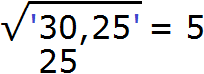
Вычитаем из числа 30 число 25, получаем 5.
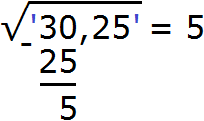
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 30,25 с точностью до целых, получили ответ 5. Последний остаток 5 показывает, что целая часть 30 превосходит квадрат 52 на 5 квадратных единиц.
Чтобы дальше извлечь корень (с точностью до десятых), снесём следующую грань, а именно число 25, получим остаток 525. А в ответе после числа 5 следует поставить запятую, поскольку сейчас мы будем искать дробную часть корня.
Затем снóсим следующую грань, а именно число 25. Получаем остаток 525
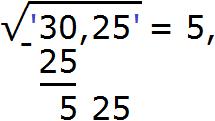
Далее работаем по тому же принципу, что и раньше. Нахóдим следующую цифру корня. Для этого уже найденный корень, а именно число 5 умножим на 2 получим 10. К числу 10 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 525 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 5. Допишем её к числу 10 и умножим получившееся число 105 на ту же самую дописанную цифру 5
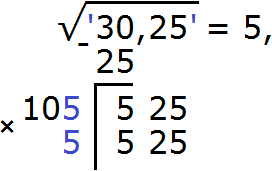
Получилось число 525, которое в точности является нашим остатком. Значит дописанная к числу 10 цифра 5 является следующей цифрой корня. Возвращаемся к исходному примеру и записываем цифру 5 после в ответе после запятой:
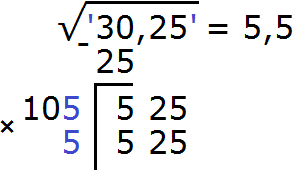
Выполняем вычитание 525 − 525 = 0. Ноль в остатке говорит о том, что решение окончено:
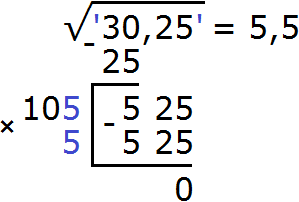
В подкоренном выражении можно было использовать следующий прием: умножить подкоренное число на 100 и получить под корнем число 3025. Далее извлечь из него квадратный корень, как из обычного целого числа. Тогда получился бы ответ 55
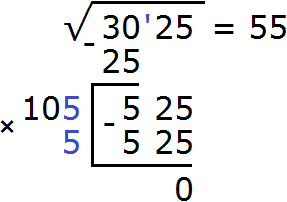
Затем можно обратно разделить 3025 на 100 (или сдвинуть запятую влево на две цифры). В результате под корнем полýчится прежнее число 30,25, а правая часть уменьшится в десять раз и полýчится квадратный корень из числа 30,25.
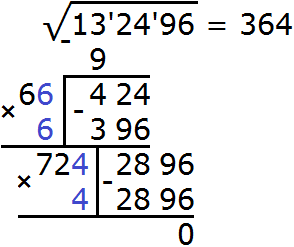
Пример 5. Извлечём квадратный корень из числа 632,5225 с помощью алгоритма извлечения квадратного корня.
Данное число является десятичной дробью. Разбиваем число на грани. На грани следует разбить целую и дробную часть. Целую часть на грани следует разбить, двигаясь влево от запятой. А дробную — двигаясь вправо от запятой:
![]()
Получилось четыре грани. При этом две грани в целой части, и две грани в дробной. Это значит, что корень будет состоять из четырёх цифр: две цифры будет в целой части корня, и две цифры после запятой.
Извлечём квадратный корень из первой грани (из числа 6) с точностью до целых, получаем 2. Записываем 2 после знака равенства:
![]()
Далее возвóдим число 2 в квадрат и полученный результат записываем под первой гранью (под числом 6)
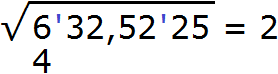
Вычитаем из числа 6 число 4, получаем 2. Затем снóсим следующую грань, а именно число 32. Получаем остаток 232
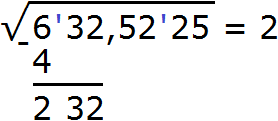
Теперь нахóдим вторую цифру корня. Первую уже найденную цифру корня, а именно 2 умножаем на 2, получаем 4. К числу 4 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня) и умножить получившееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 232 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 6. Допишем её к числу 4 и умножим получившееся число 46 на ту же самую дописанную цифру 6. Результат умножения будем записывать сразу под остатком 232
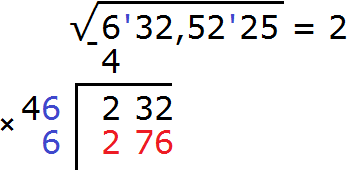
Получилось число 276, которое больше остатка 232. Значит цифра 6 не годится в качестве второй цифры корня. Проверим тогда цифру 5. Допишем ее к числу 4 и умножим получившееся число 45 на на ту же самую дописанную цифру 5
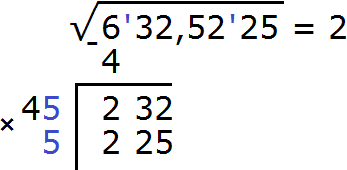
Получилось число 225, которое не превосходит остатка 232. Значит дописанная к числу 4 цифра 5 является второй цифрой корня. Записываем её в ответе после цифры 2
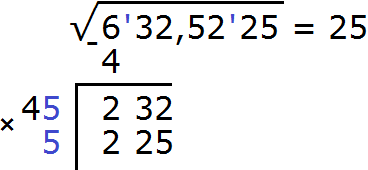
Теперь выполняем вычитание 232 − 225 = 7.
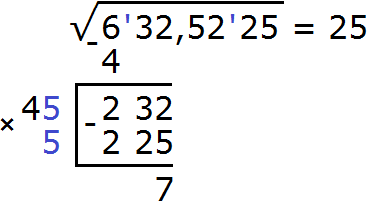
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 632,5225 с точностью до целых, получили ответ 25. Последний остаток 7 показывает, что целая часть 632 превосходит квадрат 252 на 7 квадратных единиц.
Чтобы дальше извлечь корень (с точностью до десятых и сотых), снесём следующую грань, а именно число 52, получим остаток 752. А в ответе после числа 25 поставим запятую, поскольку сейчас мы будем искать дробные части корня:
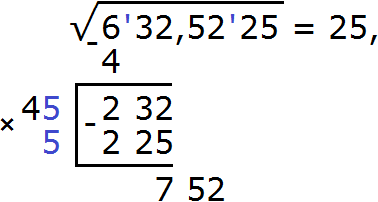
Далее работаем по тому же принципу, что и раньше. Нахóдим первую цифру корня после запятой. Для этого уже найденные цифры, а именно 25 умножим на 2 получим 50. К числу 50 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 752 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 50 и умножим получившееся число 502 на ту же самую дописанную цифру 2. Можно интуитивно понять, что цифра 2 великá, поскольку 502 × 2 = 1004. А число 1004 больше остатка 752. Тогда очевидно, что первой цифрой после запятой будет цифра 1
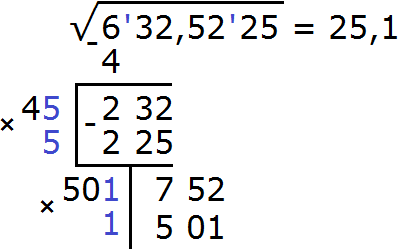
Теперь выполняем вычитание 752 − 501 = 251. Сразу снóсим следующую грань 25. Полýчим остаток 25125

Теперь нахóдим вторую цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умнóжим на 2. Полýчим 502.
К числу 502 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 25125 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 6. Допишем её к числу 502 и умнóжим образовавшееся число 5026 на ту же самую дописанную цифру 6. Результат умножения будем записывать сразу под остатком 25125

Получилось число 30156, которое больше остатка 25125. Значит цифра 6 не годится в качестве второй цифры корня после запятой. Проверим тогда цифру 5. Допишем ее к числу 502 и умножим получившееся число 5025 на на ту же самую дописанную цифру 5
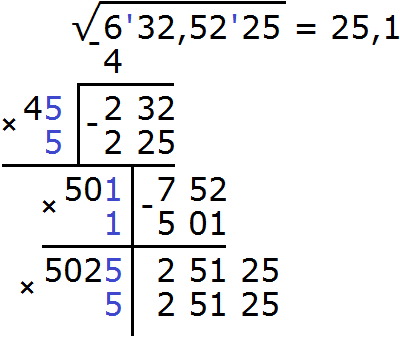
Получилось число 25125, которое в точности является нашим остатком. Значит дописанная к числу 502 цифра 5 является второй цифрой корня после запятой. Записываем цифру 5 в ответе после цифры 1

Теперь выполняем вычитание 25125 − 25125 = 0. Ноль в остатке говорит о том, что решение окончено:
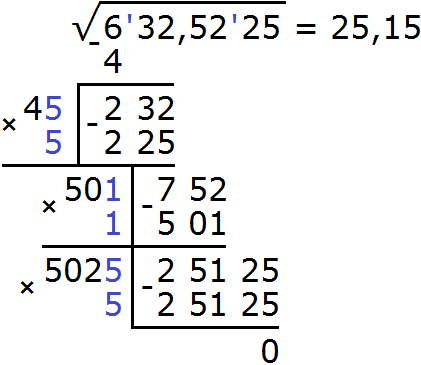
В этом примере можно было воспользоваться методом умножения подкоренного выражения на 10000. Тогда подкоренное число приняло бы вид 6325225. Его можно разделить на грани, двигаясь справа налево. В результате получился бы корень 2515
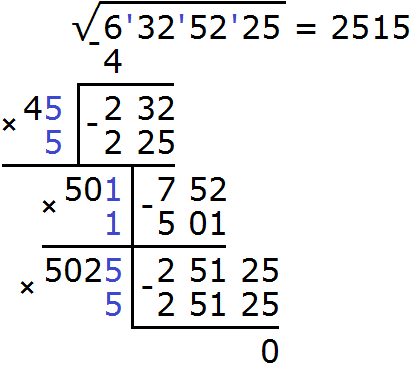
Затем подкоренное число 6325225 делят на 10000, чтобы вернуться к изначальному числу 632,5225. В результате этого деления ответ умéньшится в 100 раз и обратится в число 25,15.
Пример 4. Используя алгоритм извлечения квадратного корня, извлечь квадратный корень из числа 11 с точностью до тысячных:
В данном числе только одна грань 11. Извлечём из неё корень с точностью до целых, получим 3
![]()
Теперь возвóдим число 3 в квадрат и полученный результат записываем под первой гранью (под числом 11)
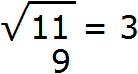
Выполним вычитание 11 − 9 = 2
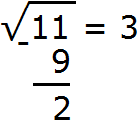
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 11 с точностью до целых, получили ответ 3. Последний остаток 2 показывает, что целая часть 11 превосходит квадрат 32 на две квадратные единицы.
Наша задача была извлечь корень из числа 11 с точностью до тысячных. Значит нужно снести следующую грань, но её в данном случае нет.
Если после целого числа поставить запятую и написать сколько угодно нулей, то значение этого числа не измéнится. Так, после 11 можно поставить запятую и написать несколько нулей (несколько граней), которые в последствии можно будет снóсить к остаткам.
Если корень извлекáется с точностью до тысячных, то в ответе после запятой должно быть три цифры. Поэтому в подкоренном выражении поставим запятую и запишем три грани, состоящие из нулей:
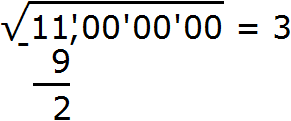
Теперь можно снести следующую грань, а именно два нуля. Получим остаток 200. А в ответе после числа 3 поставим запятую, поскольку сейчас мы будем искать дробные части корня:
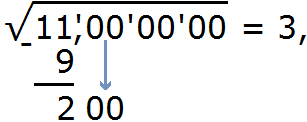
Теперь нахóдим первую цифру после запятой в ответе. Первую найденную цифру корня, а именно число 3 умножаем на 2, получаем 6. К числу 6 нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 200 или хотя бы максимально близким к нему, но не превосходящим его.
В данном случае подойдёт цифра 3
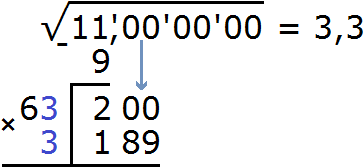
Выполним вычитание 200 − 189 и снесём следующую грань 00
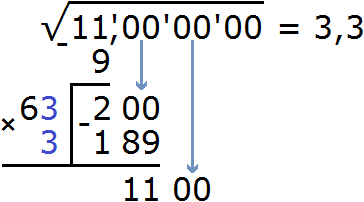
Нахóдим вторую цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умнóжим на 2. Полýчим 66.
К числу 66 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 1100 или хотя бы максимально близким к нему, но не превосходящим его.
В данном случае подойдёт цифра 1
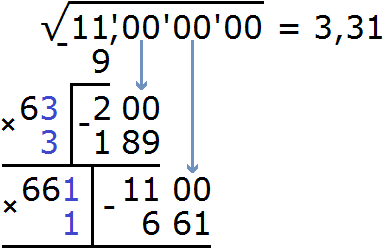
Выполним вычитание 1100−661 и снесём следующую грань 00
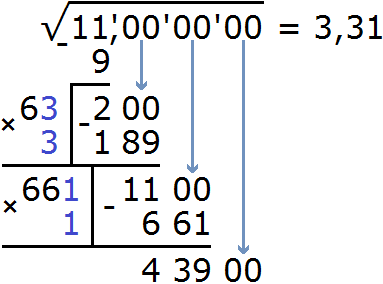
Нахóдим третью цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умножим на 2. Получим 662.
К числу 662 нужно дописáть ещё одну цифру (эта цифра впоследствии и станет третьей цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 43900 или хотя бы максимально близким к нему, но не превосходящим его.
Проверим цифру 7
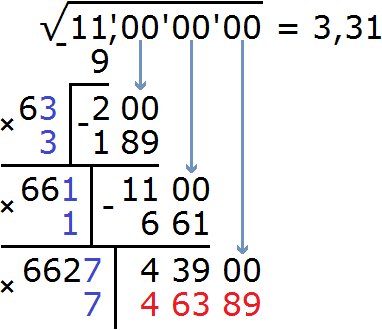
Получилось число 46389, которое больше остатка 43900. Значит цифра 7 не годится в качестве третьей цифры корня после запятой. Проверим тогда цифру 6. Допишем ее к числу 662 и умножим получившееся число 6626 на на ту же самую дописанную цифру 6

Получилось число 39756, которое не превосходит остатка 43900. Значит дописанная к числу 662 цифра 6 является третьей цифрой корня после запятой. Записываем цифру 6 в ответе после цифры 1
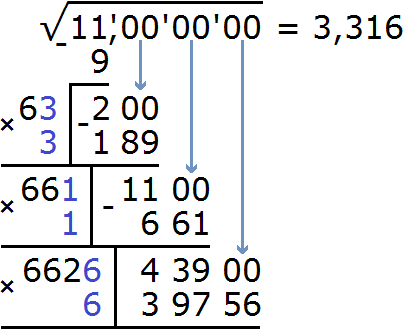
Выполним вычитание 43900 − 39756 = 4144
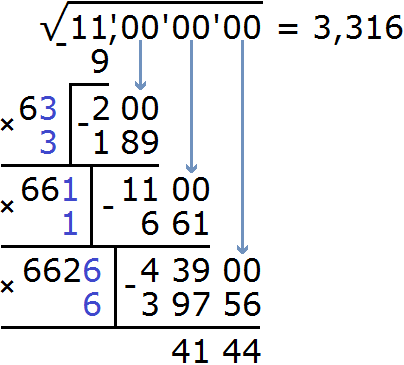
Дальнейшее вычисление не требуется, поскольку корень нужно было извлечь с точностью до тысячных.
Но в таких примерах как этот, цифры после запятой можно находить бесконечно. Например, так можно продолжить данный пример, найдя значение корня с точностью до десятитысячных:

Как работает алгоритм
Алгоритм извлечения квадратного корня основан на формуле квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Геометрически эту формулу можно представить так:
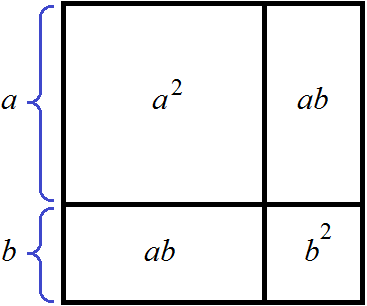
То есть сторона a увеличивается на b. Это приводит к увеличению изначального квадрата. Чтобы вычислить площадь такого квадрата, нужно по отдельности вычислить площади квадратов и прямоугольников, входящих в этот квадрат и сложить полученные результаты. Важно хорошо понимать данный рисунок. Без его понимания невозможно понять как работает алгоритм извлечения квадратного корня.
Отметим, что формула квадрата суммы двух выражений позволяет возвести в квадрат любое число. Используя разряды, исходное число представляют в виде суммы чисел и далее эту сумму возвóдят в квадрат.
Например, так можно возвести число 21 в квадрат: представить данное число в виде суммы двух десятков и одной единицы, и далее эту сумму возвести в квадрат :
212 = (20 + 1)2 = 202 + 2 × 20 × 1 + 12 = 400 + 40 + 1 = 441
Геометрически это будет выглядеть так: сторона квадрата равная 21 разбивается на две составляющие: 20 и 1.
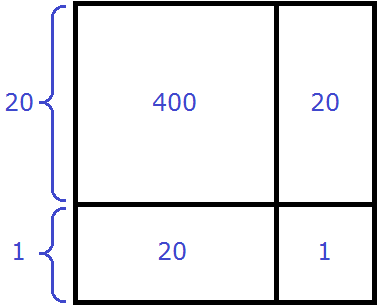
Затем по отдельности вычисляются площади квадратов и прямоугольников, входящих в большой квадрат. А именно: один квадрат со стороной 20 (получается площадь, равная 400), два прямоугольника со сторонами 20 и 1 (получается две площади по 20), один квадрат со стороной 1 (получается площадь, равная 1). Результаты вычисления площадей складываются и получается итоговое значение 441.
Заметим также, что при возведéнии десятков в квадрат получились сотни. В данном случае при возведéнии числа 20 в квадрат получилось число 400. Это позволяет предположить, что если корень является двузначным числом, то десятки этого корня следует искать в сотнях подкоренного числа. Действительно, ![]() . Десятки корня это цифра 2, является корнем числа 4, которое отвечает за сотни числа 441.
. Десятки корня это цифра 2, является корнем числа 4, которое отвечает за сотни числа 441.
А при возведéнии сóтен в квадрат получаются десятки тысяч. Например, возведём в квадрат число 123, используя формулу квадрата суммы двух выражений. Число 123 это одна сотня, два десятка и три единицы:
1232 = (100 + 20 + 3)2
При изучении многочленов мы выяснили, что если многочлен содержит более двух членов и возникла необходимость применить формулу квадрата суммы, то некоторые из членов можно взять в скобки, чтобы получилось выражение вида (a + b)2
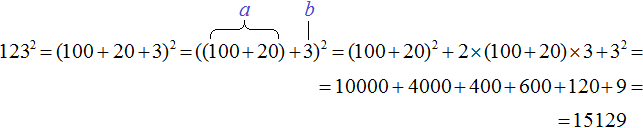
Рассмотрим подробное извлечение квадратного корня из числа 4096. Заодно пройдёмся по основным этапам алгоритма извлечения квадратного корня, рассмотренного в предыдущей теме.
Допустим, что число 4096 это площадь следующего квадрата:
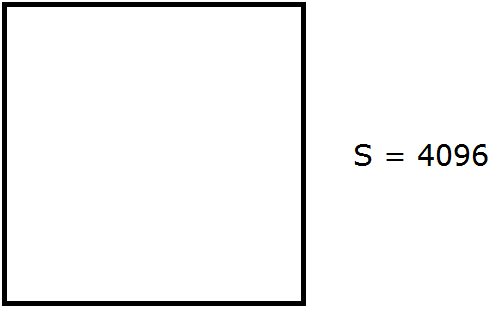
Извлечь корень из числа 4096 означает найти длину стороны данного квадрата:
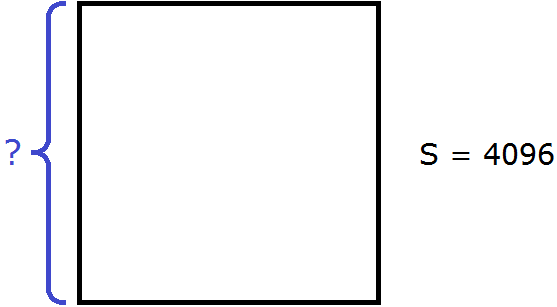
Для начала узнáем из скольких цифр будет состоять корень. Ближáйшие от 4096 известные нам квадраты это 3600 и 4900. Между ними располагается квадрат 4096. Запишем это в виде неравенства:
![]()
Запишем каждое число под знáком корня:
![]()
Квадратные корни из чисел 3600 и 4900 нам известны. Это корни 60 и 70 соответственно:
![]()
Корни 60 и 70 являются двузначными числами. Если квадратный корень из числа 4096 располагается между числами 60 и 70, то этот корень тоже будет двузначным числом.
Двузначное число состоит из десятков и единиц. Это значит, что квадратный корень из числа 4096 можно представить в виде суммы a + b, где a — десятки корня, b — единицы корня. Сумма a + b во второй степени будет равна 4096
(a + b)2 = 4096
Тогда сторона квадрата будет разбита на две составляющие: a и b
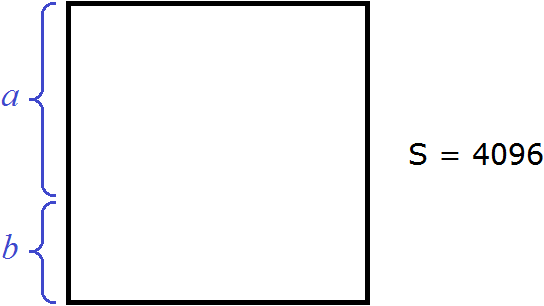
Перепишем в равенстве (a + b)2 = 4096 левую часть в виде a2 + 2ab + b2
a2 + 2ab + b2 = 4096
Тогда рисунок, иллюстрирующий квадрат площадью 4096, можно представить так:
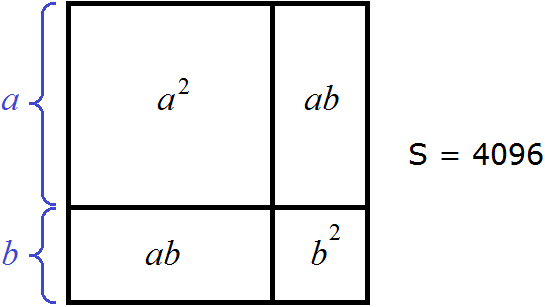
Если мы узнáем значения переменных a и b, то узнáем длину стороны данного квадрата. Проще говоря, узнáем сам корень.
Вернёмся к извлечению корня. Мы выяснили, что корнем будет двузначное число. Двузначное число состоит из десятков и единиц. При возведéнии десятков в квадрат, получаются сотни. Тогда десятки искомого корня следует искать в сотнях подкоренного числа. В подкоренном числе 40 сотен. Отделим их небольшой помéткой:
![]()
Извлечём корень из числа 40. Из числа 40 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых.
Ближáйший мéньший квадрат к числу 40 это 36. Извлечём корень из этого квадрата, получим 6. Тем сáмым полýчим первую цифру корня:
![]()
На самом деле корень извлечён не из числа 40, а из сорокá сотен. Метка, которая постáвлена после числа 40, отделяет разряды числа, находящегося под знáком корня. Нужно понимать, что в данном случае 40 это 4000.
Из 4000 как и из 40 корень не извлекается, поэтому его тоже следует извлекать приближённо. Для этого следует найти ближáйший мéньший квадрат к числу 4000. Но нужно принимать во внимание следующий момент. Десятки это числа с одним нулем на конце. Примеры:
10 — один десяток
30 — три десятка
120 — двенадцать десятков
При возведéнии таких чисел в квадрат, получаются числа с двумя нулями на конце:
102 = 100
302 = 900
1202 = 14400
Мы ищем десятки корня в сотнях числá 4096, то есть в числе 4000. Но нет такого числá с нулем на конце, вторая степень которого равна 4000. Поэтому мы ищем ближáйший мéньший квадрат, но опять же с двумя нулями на конце. Таковым является квадрат 3600. Корень следует извлекать из этого квадрата.
Вернемся к нашему рисунку. Большой квадрат со стороной a и площадью a2 это тот самый квадрат 3600. Укажем вместо a2 значение 3600
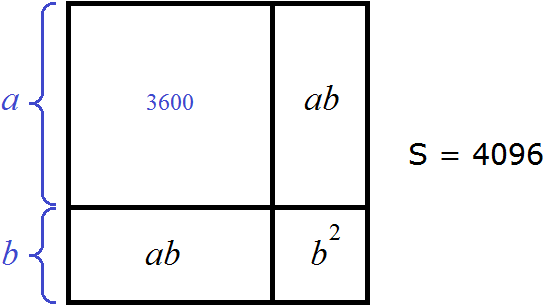
Теперь извлечём квадратный корень из квадрата 3600. Ранее мы говорили, что если число содержит уже знакомый нам квадрат и чётное количество нулей, то можно извлечь корень из этого числа. Для этого сначала следует извлечь корень из знакомого нам квадрата, а затем записать половину от количества нулей исходного числа:
![]()
Итак, мы нашли сторону квадрата, площадь которого 3600. Подпишем сторону a как 60
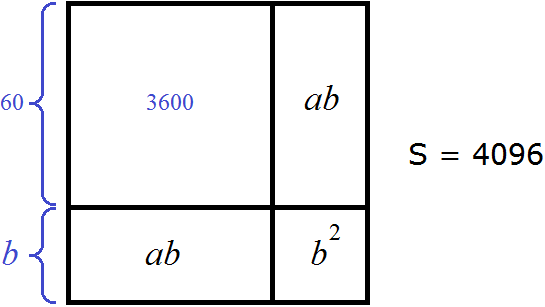
Но ранее в ответе мы написали не 60, а 6. Это является сокращённым вариантом. Число 6 в данном случае означает шесть десятков:
![]()
Итак, десятки корня найдены. Их шесть. Теперь нужно найти единицы корня. Единицы корня это длина оставшейся маленькой стороны квадрата, то есть значение переменной b.
Чтобы найти b, нужно из общего квадрата, площадь которого 4096 вычесть квадрат, площадь которого 3600. В результате останется фигура, площадь которой 4096 − 3600 = 496
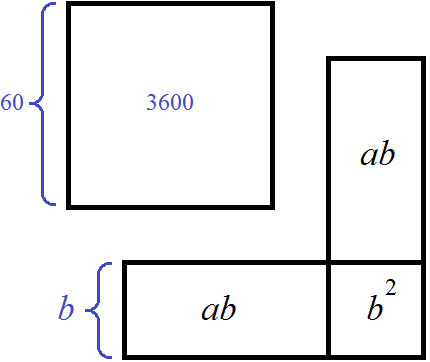
На рисунке видно как из квадрата, площадь которого 4096 отделился квадрат, площадь которого 3600. Осталась фигура, площадь которой 496.
Именно поэтому в процессе применения алгоритма первая найденная цифра корня возводится в квадрат, чтобы результат возведения вычесть из сотен подкоренного выражения.
Так, из 40 сотен вычитаются 36 сотен, остаётся 4 сотни плюс сносятся девяносто шесть единиц. Эти четыре сотни и девяносто шесть единиц вместе образуют 496 единиц:
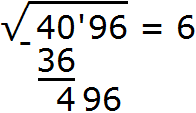
Оставшаяся фигура есть ни что иное как удвоенное произведение первого выражение a плюс квадрат второго выражения b
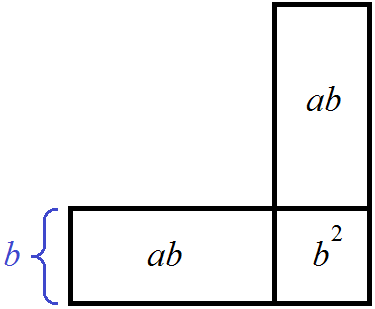
Сумма площадей 2ab + b2 должна вмещаться в число 496. Запишем это в виде следующего равенства:
2ab + b2 = 496
Значение a уже известно. Оно равно 60. Тогда равенство примет вид:
2 × 60 × b + b2 = 496
120b + b2 = 496
Теперь наша задача найти такое значение b, при котором левая часть станет равна 496 или хотя близкой к этому числу. Поскольку b является единицами искомого корня, то значение b является однозначным числом. То есть значение b это число от 1 до 9. Это число можно найти методом подбора. В данном случае очевидно, что числом b является 4
120 × 4 + 42 = 496
480 + 16 = 496
496 = 496
Но для удобства поиска этой цифры, переменную b выносят за скобки. Вернёмся к выражению 120b + b2 = 496 и вынесем b за скобки:
b(120 + b) = 496
Теперь правую часть можно понимать так: к 120 следует прибавить некоторое число b, которое при умножении с тем же сáмым b даст в результате 496.
Именно поэтому при использовании алгоритма, уже найденную цифру умножают на 2. Так, 6 мы умножили на 2 получили 12 и уже к 12 дописывали цифру и умножáли образовавшееся число на ту же дописанную цифру, пытаясь получить остаток 496.
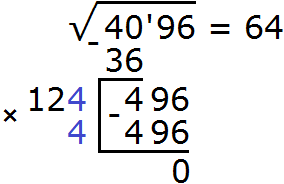
Но это опять же упрощённый вариант. На самом деле на 2 умножается не просто 6, а найденные десятки (в нашем случае число 60), получается число 120. Затем следует нахождение числá вида b(120 + b). То есть к 120 прибавляется число b, которое при перемножении с b даёт остаток 496.
Итак, b = 4. Тогда:
4(120 + 4) = 496
4 × 124 = 496
496 = 496
При подстановке числá 4 вместо b получается остаток 496. Это значит, что единицы корня найдены. Квадрат, площадь которого 4096, имеет сторону равную 60 + 4, то есть 64.
![]()
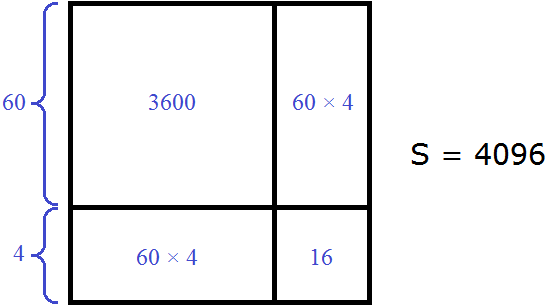
Если из общей площади вычесть 3600, затем 496, полýчим 0. Остаток, равный нулю, говорит о том, что решение завершено:
4096 − 3600 − 496 = 0
Пример 2. Извлечь квадратный корень из числа 54756
Пусть число 54756 это площадь следующего квадрата:
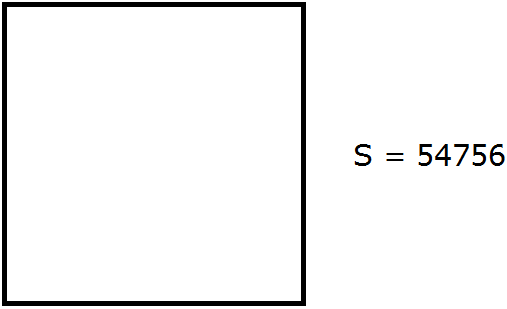
Извлечь корень из числа 54756 означает найти длину стороны данного квадрата:
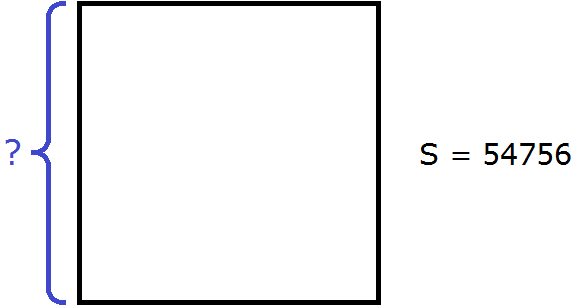
Пока неизвестно является ли квадратный корень из числа 54756 целым либо дробным числом. Узнáем для начала из скольких цифр будет состоять целый корень.
Число 54756 больше числá 10000, но меньше числá 90000
10000 < 54756 < 90000
Корни из 10000 и 90000 являются трёхзначными числами.
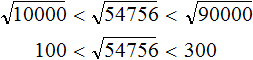
Тогда корень из 54756 тоже будет трёхзначным числом. А трёхзначное число состоит из сотен, десятков и единиц.
Квадратный корень из числа 54756 можно представить в виде суммы a + b + с, где a — сотни корня, b — десятки корня, с — единицы корня. Сумма a + b + с во второй степени будет равна 54756
(a + b + c)2 = 54756
Тогда сторона квадрата будет разбита на три составляющие: a, b и c
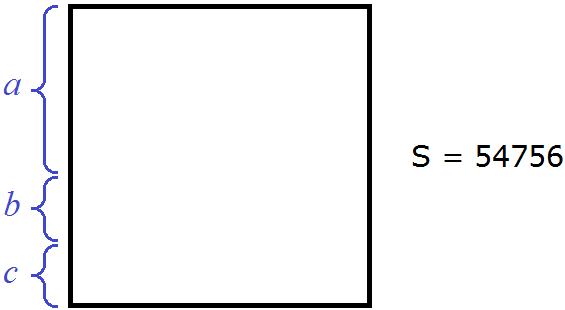
Выполним в левой части равенства (a + b + c)2 = 54756 возведéние в квадрат:
![]()
Тогда рисунок иллюстрирующий квадрат, площадью 54756 можно представить так:
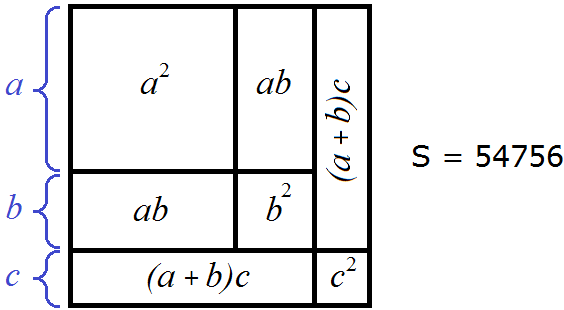
Два прямоугольника площадью ab в приведённом ранее равенстве заменены на 2ab, а два прямоугольника площадью (a + b)c заменены на 2ac + 2bc, поскольку (a + b)c = ac + bc. Если повторить выражение ac + bc дважды, то полýчится 2ac + 2bc
2(ac + bc) = 2ac + 2bc
Если мы узнáем значения переменных a, b и c, то узнáем длину стороны данного квадрата. Проще говоря, узнáем сам корень.
Вернёмся к извлечению корня. Мы выяснили, что корнем будет трёхзначное число. Трёхзначное число состоит из сотен, десятков и единиц.
При возведéнии сотен в квадрат, получаются десятки тысяч. Тогда сотни искомого корня следует искать в десятках тысяч подкоренного числа. В подкоренном числе 5 десятков тысяч. Отделим их мéткой:
![]()
Извлечём корень из числа 5. Из числа 5 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых Ближáйший мéньший квадрат к 5 это 4. Извлечём корень из этого квадрата, получим 2. Тем самым полýчим первую цифру корня:
![]()
На самом деле корень извлечён не из числа 5, а из пяти десятков тысяч. Метка, которая поставлена после числá 5, отделяет разряды числá, находящегося под знáком корня. Нужно понимать, что в данном случае 5 это 50000.
Из 50000 как и 5 корень не извлекается, поэтому его тоже следует извлекать приближённо. Для этого следует найти ближáйший мéньший квадрат к числу 50000. Но нужно принимать во внимание, что сотни это числа с двумя нулями на конце. Примеры:
100 — одна сотня
500 — пять сотен
900 — девять сотен
При возведéнии таких чисел в квадрат, получаются числа, у которых четыре нуля на конце:
1002 = 10000
5002 = 250000
9002 = 810000
Мы ищем сотни корня в десятках тысяч числа 54756, то есть в числе 50000. Но нет такого числá с двумя нулями на конце, вторая степень которого равна 50000. Поэтому мы ищем ближáйший мéньший квадрат, но опять же с четырьмя нулями на конце. Таковым является квадрат 40000.
Вернёмся к нашему рисунку. Большой квадрат со стороной a и площадью a2 это тот самый квадрат 40000. Укажем вместо a2 значение 40000
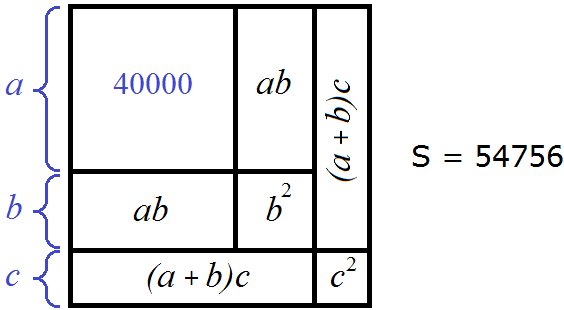
Теперь извлечём корень из квадрата 40000
![]()
Итак, мы нашли сторону квадрата, площадь которого 40000. Подпишем сторону a как 200
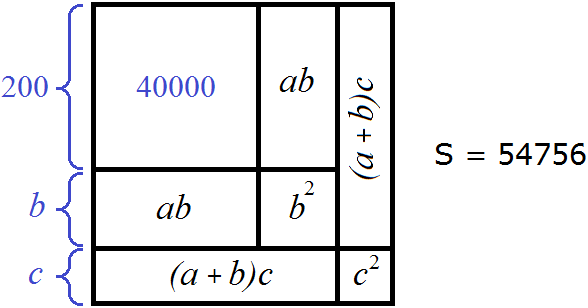
Но ранее в ответе мы написали не 200, а 2. Это является сокращённым вариантом. Число 2 в данном случае означает две сотни:
![]()
Теперь вытаскиваем остаток. Из пяти десятков тысяч корень извлечён только из четырёх десятков тысяч. Значит в остатке остался один десяток тысяч. Вытащим его:
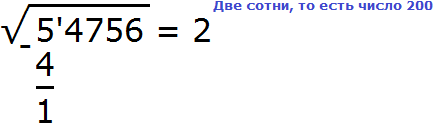
Опять же надо понимать, что 4 это 40000, а 1 это 10000. С помощью рисунка это можно пояснить так: квадрат, площадь которого 40000, вычитается от общего квадрата, площадь которого 54756. Остаётся фигура, площадь которой 54756 − 40000 = 14756
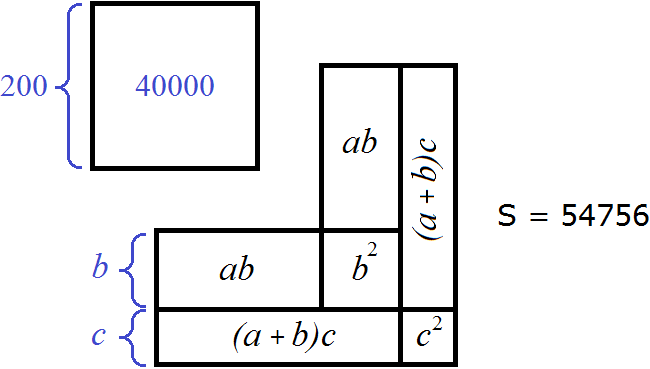
Теперь нужно найти десятки корня. Рассмотрим на рисунке сумму площадей ab + ab + b2 (или 2ab + b2). В эту сумму будет входить один десяток тысяч, который остался в результате нахождения сóтен корня, удвоенное произведение сотен и десятков корня 2ab, а также десятки корня в квадрате b2.
Десятки в квадрате составляют сотни. Поэтому десятки корня следует искать в сотнях подкоренного числа. Под корнем сейчас 47 сотен. Снесём их к остатку 1, предварительно отделив их под корнем мéткой:
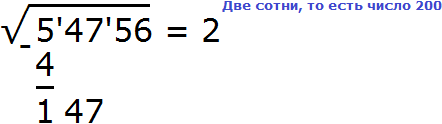
Один десяток тысяч это сто сотен, плюс снесено 47 сотен. Итого 100 + 47 = 147 сотен. В эти 147 сотен должна входить сумма 2ab + b2
2ab + b2 = 14700
Переменная a уже известна, она равна 200. Подставим это значение в данное равенство:
2 × 200 × b + b2 = 14700
400b + b2 = 14700
Теперь наша задача найти такое значение b, при котором левая часть станет равна 14700 или хотя близкой к этому числу, но не превосходящей его. Поскольку b является десятками искомого корня, то значение b является двузначным числом с одним нулём на конце. Такое число можно найти методом подбора. Для удобства вынесем в левой части за скобки b
b(400 + b) = 14700
Теперь левую часть можно понимать так: к 400 следует прибавить некоторое число b, которое при умножении с тем же самым b даст в результате 14700 или близкое к 14700 число, не превосходящее его. Подставим например 40
40(400 + 40) = 14700
17600 ≠ 14700
Получается 17600, которое превосходит число 14700. Значит число 40 не годится в качестве десятков корня. Проверим тогда число 30
30(400 + 30) = 14700
12900 ≤ 14700
Получилось число 12900, которое не превосходит 14700. Значит число 30 подходит в качестве десятков корня. Числа, расположенные между 30 до 40 проверять не нужно, поскольку сейчас нас интересуют только двузначные числа с одним нулем на конце:
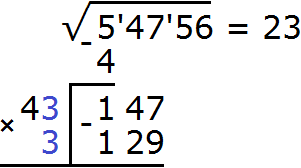
Вернемся к нашему рисунку. Сторона b это десятки корня. Укажем вместо b найденные десятки 30. А квадрат, площадь которого b2 это найденные десятки во второй степени, то есть число 900. Также укажем площади прямоугольников ab. Они равны произведению сотен корня на десятки корня, то есть 200 × 30 = 6000
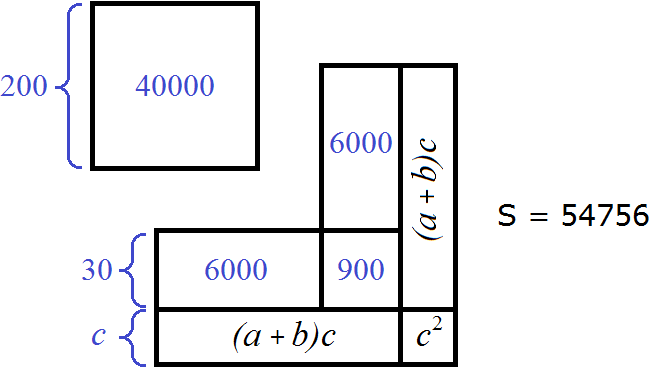
Ранее в ответе мы написали не 30, а 3. Это является сокращённым вариантом. Число 3 в данном случае означают три десятка.
Теперь вытаскиваем остаток. В 147 сотен вместилось только 129 сотен. Значит в остатке осталось 147 − 129 = 18 сотен плюс сносим число 56 из подкоренного выражения. В результате образýется новый остаток 1856
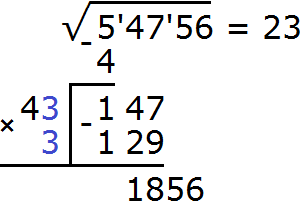
С помощью рисунка это можно пояснить так: от фигуры, площадь которой 14756, вычитается площадь 12900. Остаётся фигура, площадь которой 14756 − 12900 = 1856
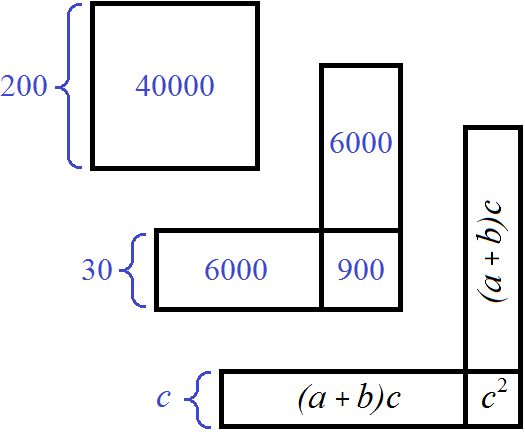
Теперь нужно найти единицы корня. Рассмотрим на рисунке сумму площадей 2(a + b)c + c2. В эту сумму и должен входить последний остаток 1856
2(a + b)c + c2 = 1856
Переменные a и b уже известны, они равны 200 и 30 соответственно. Подставим эти значения в данное равенство:
2(200 + 30)c + c2 = 1856
2 × 230c + c2 = 1856
460c + c2 = 1856
Теперь наша задача найти такое значение c, при котором левая часть станет равна 1856 или хотя близкой к этому числу, но не превосходящей его. Поскольку c является единицами искомого корня, то значение с является однозначным числом. То есть значение с это число от 1 до 9. Это число можно найти методом подбора. Для удобства вынесем в левой части за скобки с
с(460 + c) = 1856
Теперь левую часть можно понимать так: к 460 следует прибавить нéкоторое число с, которое при умножении с тем же сáмым с даст в результате 1856 или близкое к 1856 число, не превосходящее его. Подставим, например, число 4
4(460 + 4) = 1856
4 × 464 = 1856
1856 = 1856
Именно поэтому при использовании алгоритма первые найденные цифры умножают на 2. Так, 23 мы умнóжили на 2, получили 46 и уже к 46 дописывали цифру и умножáли образовавшееся число на ту же самую дописанную цифру, пытаясь получить остаток 1856
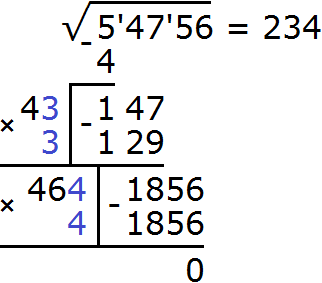
Итак, с = 4. При подстановке вместо с числá 4 получается остаток 1856. Это значит, что единицы корня найдены.
Квадрат, площадь которого 54756, имеет сторону равную 200 + 30 + 4, то есть 234.
![]()
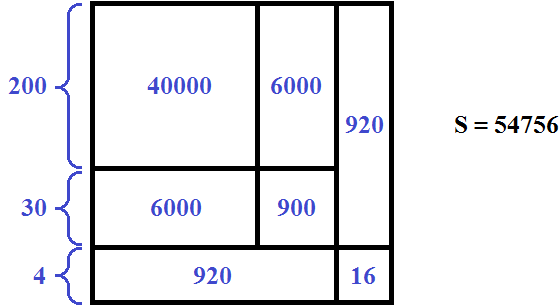
Если из общей площади 54756 вычесть 40000, 6000, 6000, 900, 920, 920 и 16, то получим 0. Остаток равный нулю говорит о том, что решение завершено:
54756 − 40000 − 6000 − 6000 − 900 − 920 − 920 − 16 = 0
Пример 3. Извлечь квадратный корень из числа 3
Квадратный корень из числа 3 не извлекается. Ранее мы говорили, что квадратные корни из таких чисел можно извлекать только приближённо с определенной точностью.
Пусть 3 это площадь следующего квадрата:

Извлечь корень из числа 3 значит найти длину стороны данного квадрата:

Корень из 3 больше корня из 1, но меньше корня из 4
√1 < √3 < √4
Корни из 1 и 4 являются целыми числами.
√1 < √3 < √4
1 < √3 < 2
Между числами 1 и 2 нет целых чисел. Значит корень из числа 3 будет десятичной дробью. Найдём этот корень с точностью до десятых.
Квадратный корень из числа 3 можно представить в виде суммы a + b, где a — целая часть корня, b — дробная часть. Тогда сторону квадрата можно разбить на две составляющие: a и b

Сумма a + b во второй степени должна приближённо равняться 3.
(a + b)2 ≈ 3
Выполним в левой части данного равенства возведéние в квадрат:
a2 + 2ab + b2 ≈ 3
Тогда рисунок, иллюстрирующий квадрат площадью 3, можно представить так:
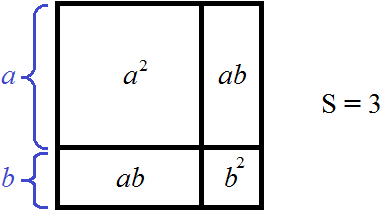
Найдём a. Извлечём корень из числа 3 с точностью до целых, получим 1
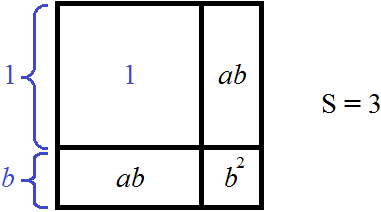
Если a2 это 1, а площадь всего квадрата равна 3, то в остатке останется 2. В этот остаток должна вмещаться площадь оставшейся фигуры:
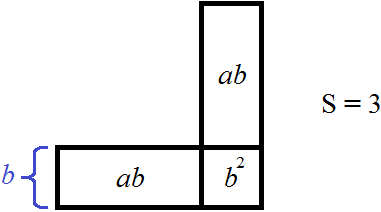
Найдём b. Для этого рассмотрим сумму площадей 2ab + b2. Эта сумма должна приближённо равняться остатку 2, но не превосходить его
2ab + b2 ≈ 2
Значение a уже известно, оно равно единице:
2b + b2 ≈ 2
Вынесем за скобки b
b(2 + b) ≈ 2
Теперь в левой части к 2 следует прибавить нéкоторое число b, которое при умножении с тем же b будет приближённо равняться 2.
Значение b является дробным числом, а именно десятой частью. Оно равно какому-нибудь числу из промежутка [0,1; 0,9]. Возьмём любое число из этого промежутка и подставим его в равенство. Подставим к примеру 0,8
0,8(2 + 0,8) ≈ 2
2,24 ≈ 2
Получилось 2,24 которое превосходит 2. Значит 0,8 не годится в качестве значения b. Проверим тогда 0,7
0,7(2 + 0,7) ≈ 2
1,89 ≈ 2
Получилось 1,89 которое приближённо равно 2 и не превосходит его. Значит 0,7 является значением b
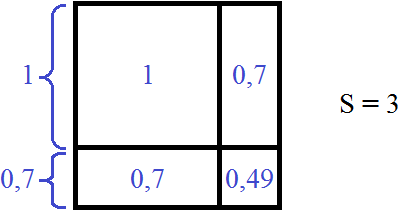
Значит квадратный корень из 3 с точностью до десятых приближённо равен 1 + 0,7
![]()
К сожалению, понять механизм алгоритма извлечения квадратного корня намного сложнее, чем использовать сам алгоритм. Решите несколько примеров на применение алгоритма, и понимание механизма его работы будет даваться вам значительно проще.
Задания для самостоятельного решения
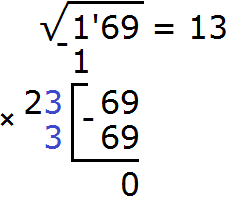
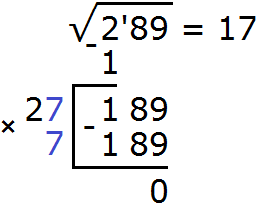
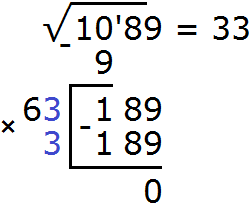
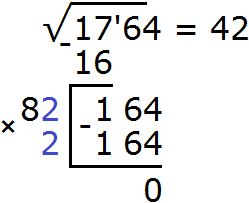
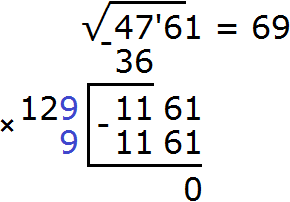
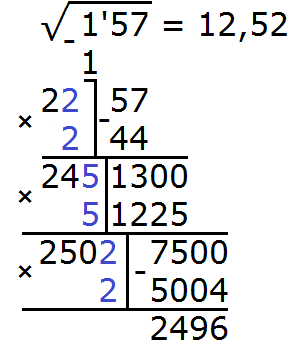
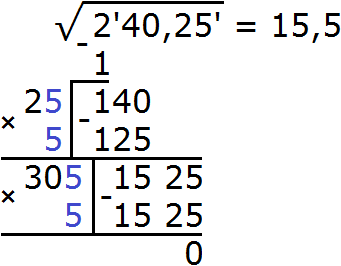
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Квадратный корень
Основные сведения
Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.
Найдём площадь квадрата, длина стороны которого 3 см
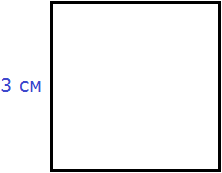
S = 32 = 9 см2
Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.
Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.
Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.
Введём для работы с корнями новые обозначения.
Символ кóрня выглядит как ![]() . Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня
. Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня ![]() .
.
Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)
![]()
Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)
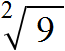
Получили выражение, которое читается так: «квадратный корень из числа 9». С этого момента возникает новая задача по поиску самогó корня.
Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:
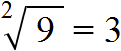
Значит квадрат площадью 9 см2 имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня.
Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9
![]()
Получается, что выражение ![]() имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.
Например, извлечём квадратный корень из числа 4
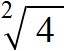
Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4
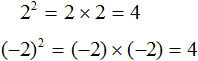
Поэтому ответ к выражению вида ![]() записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
Запишем ответ к выражению ![]() с плюсом и минусом:
с плюсом и минусом:
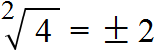
Определения
Дадим определение квадратному корню.
Квадратным корнем из числа a называют такое число b, вторая степень которого равна a.
То есть число b должно быть таким, чтобы выполнялось равенство b2 = a. Число b (оно же корень) обозначается через радикал ![]() так, что
так, что ![]() . На практике левая и правая часть поменяны местами и мы видим привычное выражение
. На практике левая и правая часть поменяны местами и мы видим привычное выражение ![]()
Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16
42 = 16
Корень 4 можно обозначить через радикал ![]() так, что
так, что ![]() .
.
Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16
(−4)2 = 16
Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным.
Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b2 = a.
В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.
В разговорном языке можно использовать сокращение. К примеру, выражение ![]() полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
Не следует путать понятия корень и квадрат. Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно.
Корнями же являются числа 5, 6 и 7. Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно.
Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи ![]() можно использовать запись
можно использовать запись![]() . Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:
![]()
Это по причине того, что единица во второй степени равна единице:
12 = 1
и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:
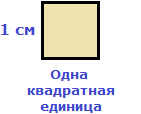
Квадратный корень из нуля равен нулю. То есть справедливо равенство ![]() , поскольку 02 = 0.
, поскольку 02 = 0.
Выражение вида ![]() смысла не имеет. Например, не имеет смысла выражение
смысла не имеет. Например, не имеет смысла выражение ![]() , поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
, поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
Если выражение вида ![]() возвести во вторую степень, то есть если записать
возвести во вторую степень, то есть если записать ![]() , то это выражение будет равно подкореннóму выражению a
, то это выражение будет равно подкореннóму выражению a
![]()
Например, выражение ![]() равно 4
равно 4
![]()
Это потому что выражение ![]() равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
Еще примеры:
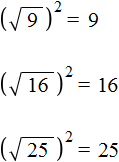
Корень из квадрата числá равен модулю этого числá:
![]()
Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5
![]()
Это же правило будет срабатывать, если во вторую степень возвóдится отрицательное число. То есть, ответ опять же станет положительным. Например, корень из числá −5, возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5
![]()
Действительно, если не пользуясь правилом ![]() , вычислять выражение
, вычислять выражение ![]() обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
![]()
Не следует путать правило ![]() с правилом
с правилом ![]() . Правило
. Правило ![]() верно при любом a, тогда как правило
верно при любом a, тогда как правило ![]() верно в том случае, если выражение
верно в том случае, если выражение ![]() имеет смысл.
имеет смысл.
В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:
![]()
Примеры: √4, √9, √16.
Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.
Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.
49 < 64
Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7, а √64 = 8,
√49 < √64
Отсюда:
7 < 8
Примеры извлечения квадратных корней
Рассмотрим несколько простых примеров на извлечение квадратных корней.
Пример 1. Извлечь квадратный корень √36
Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 62 = 36
√36 = 6
Пример 2. Извлечь квадратный корень √49
Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 72 = 49
√49 = 7
В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:
7 × 7 = 49
Но 7 × 7 это 72
72 = 49
Отсюда, √49 = 7.
Пример 3. Извлечь квадратный корень √100
Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10, поскольку 102 = 100
√100 = 10
Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.
Пример 3. Извлечь квадратный корень √256
Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.
Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.
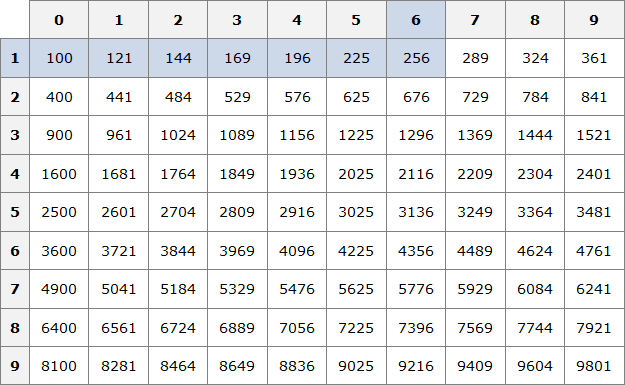
Видим, что это число 16. Значит √256 = 16.
Пример 4. Найти значение выражения 2√16
В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16, затем перемнóжим его с числом 2
![]()
Пример 7. Решить уравнение ![]()
В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.
Значение переменной x равно 16, поскольку ![]() . Значит корень уравнения равен 16.
. Значит корень уравнения равен 16.
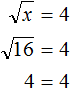
Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом ![]() .
.
Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.
Из определения мы знаем, что квадратный корень ![]() равен числу b, при котором выполняется равенство b2 = a.
равен числу b, при котором выполняется равенство b2 = a.
![]()
Применим равенство b2 = a к нашему примеру ![]() . Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем
. Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем ![]() , а именно переменная x
, а именно переменная x
![]()
В выражении 42 = x вычислим левую часть, полýчим 16 = x. Поменяем левую и правую часть местами, полýчим x = 16. В результате приходим к тому, что нашлось значение переменной x.
Пример 8. Решить уравнение ![]()
Перенесем −8 в правую часть, изменив знак:
![]()
Возведем правую часть во вторую степень и приравняем её к переменной x
![]()
Вычислим правую часть, полýчим 64 = x. Поменяем левую и правую часть местами, полýчим x = 64. Значит корень уравнения ![]() равен 64
равен 64
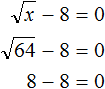
Пример 9. Решить уравнение ![]()
Воспользуемся определением квадратного корня:
![]()
Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x. Возведем число 7 во вторую степень и приравняем его к 3 + 5x
![]()
В выражении 72 = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x. Получилось обычное линейное уравнение. Решим его:
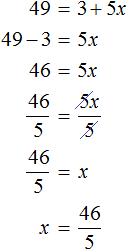
Корень уравнения ![]() равен
равен ![]() . Выполним проверку, подставив его в исходное уравнение:
. Выполним проверку, подставив его в исходное уравнение:
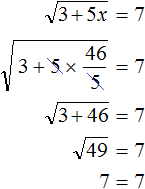
Пример 10. Найти значение выражения ![]()
В этом выражении число 2 умножается на квадратный корень из числа 49.
Сначала нужно извлечь квадратный корень и перемножить его с числом 2
![]()
Приближённое значение квадратного корня
Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.
Например, извлечь квадратный корень ![]() можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 82 = 64. То есть
можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 82 = 64. То есть ![]()
А извлечь квадратный корень ![]() нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.
Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.
Найдём значение корня ![]() приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня
приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня ![]() будет представлять собой десятичную дробь, у которой после запятой одна цифра.
будет представлять собой десятичную дробь, у которой после запятой одна цифра.
Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:
√1 = 1
Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2
√4 = 2
√1 меньше, чем √4
√1 < √4
А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:
√1 < √3 < √4
Точные значения корней √1 и √4 известны. Это числа 1 и 2
1 < √3 < 2
Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.
Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1
1,12 = 1,21
Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3, потому что оно малó.
Проверим тогда дробь 1,8
1,82 = 3,24
Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3, потому что оно великó.
Проверим тогда дробь 1,7
1,72 = 2,89
Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3. Напомним, что знак приближенного значения выглядит как ≈
√3 ≈ 1,7
Значение 1,6 проверять не нужно, потому что в результате получится число 2,56, которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим.
В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.
Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8
1,7 < √3 < 1,8
Проверим дробь 1,74
1,742 = 3,0276
Получился результат 3,0276, который близок к подкореннóму выражению, но превосходит его на 0,0276. Значит значение 1,74 великó для корня √3.
Проверим тогда дробь 1,73
1,732 = 2,9929
Получился результат 2,9929, который близок к подкореннóму выражению √3. Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых.
Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:
√3 = 1,732 (вычислено с точностью до тысячных)
√3 = 1,7320 (вычислено с точностью до десятитысячных)
√3 = 1,73205 (вычислено с точностью до ста тысячных).
Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:
√3 ≈ 1
Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.
В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.
Приближенное значение квадратного корня с недостатком или избытком
Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.
В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89. Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3.
С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24. Этот результат превосходит подкореннóе выражение на 0,24. То есть 3,24 − 3 = 0,24.
Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:
√3 ≈ 1
Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.
Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2
√3 ≈ 2
Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:
√3 ≈ 2 (с избытком)
Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.
Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых», заменяют на словосочетания «с точностью до 1», «с точностью до 0,1», «с точностью до 0,01» соответственно.
Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:
√5 ≈ 2,23
Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1
√51 ≈ 7
Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1
√51 ≈ 7,1
Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01
√51 ≈ 7,14
Границы, в пределах которых располагаются корни
Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].
Например, пусть исходным числом будет 64. Данное число принадлежит промежутку [1; 100]. Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10]. Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64? Ясно, что перемножение 8 × 8, а это есть 82 = 64. Значит квадратный корень из числа 64 есть 8
![]()
Пример 2. Извлечь квадратный корень из числа 49
Число 49 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 7, поскольку 72 = 49
√49 = 7
Пример 2. Извлечь квадратный корень из числа 1
Число 1 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 1, поскольку 12 = 1
√1 = 1
Пример 3. Извлечь квадратный корень из числа 100
Число 100 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 10, поскольку 102 = 100
√100 = 10
Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10].
Например, извлечём квадратный корень из числа 37. Нет целого числа, вторая степень которого была бы равна 37. Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых:
√37 ≈ 6,08
Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36. Квадратный корень из него равен 6. И далее отталкиваясь от числа 6, можно находить приближённое значение корня √37, проверяя различные десятичные дроби, целая часть которых равна 6.
Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
И обратно, следует знать значения квадратных корней этих квадратов:

Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.
Например, 62 = 36. Допишем к числу 6 один ноль, полýчим 60. Возведём число 60 во вторую степень, полýчим 3600
602 = 3600
А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:
6002 = 360000
Тогда можно сделать следующий вывод:
Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.
Например, извлечём квадратный корень из числа 900. Видим, что в данном числе есть знакомый нам квадрат 9. Извлекаем из него корень, получаем 3
![]()
Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3
![]()
Пример 2. Извлечём квадратный корень из числа 90000
Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:
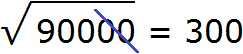
Пример 3. Извлечем квадратный корень из числа 36000000
Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:
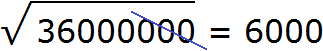
Пример 4. Извлечем квадратный корень из числа 2500
Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:
![]()
Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.
Например, ![]() . Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
. Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
![]()
И наоборот, если в равенстве ![]() уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:
уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:
![]()
Пример 2. Увеличим в равенстве ![]() подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
![]()
Пример 3. Уменьшим в равенстве ![]() подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз
подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз
![]()
Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100. Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.
Например, извлечём квадратный корень из числа 0,25. В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25.
Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:
![]()
Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве ![]() подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
![]()
Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100.
В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.
Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, ![]() .
.
Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.
Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225, квадратный корень из которого равен 35.
Тогда можно извлечь квадратный корень и из 0,1225. Умнóжим данную десятичную дробь на 10000, полýчим 1225. Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов:
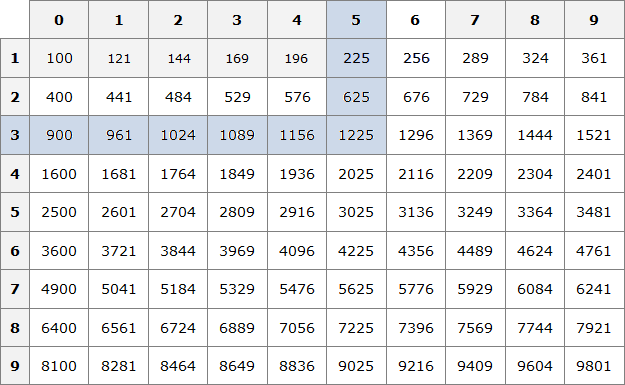
![]()
Но нам изначально нужно было извлечь корень из 0,1225, а не из 1225. Чтобы исправить ситуацию, в равенстве ![]() подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз
подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз
![]()
Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25. Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.
Умнóжим десятичную дробь 12,25 на 100, полýчим 1225. Извлечём корень из числа 1225
![]()
Теперь в равенстве ![]() уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз
уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз
![]()
Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].
В этом случае применяется таблица квадратов:
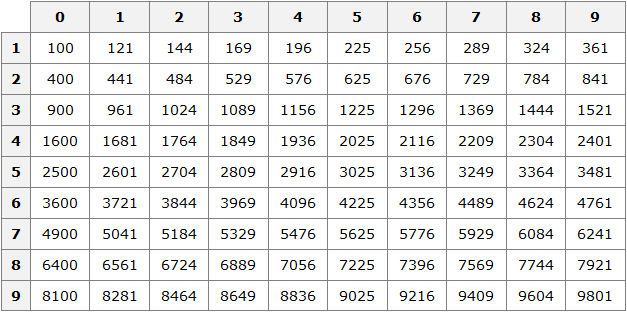
Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000]. Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100]. Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576
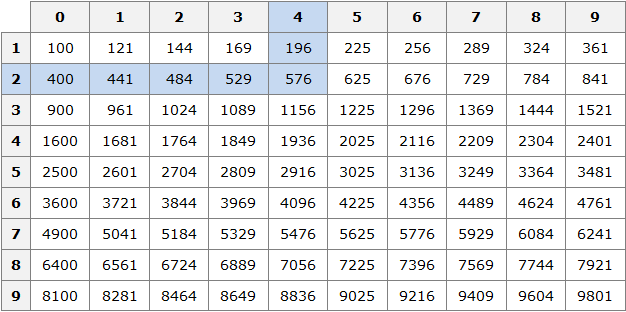
Видим, что это число 24. Значит ![]() .
.
Пример 2. Извлечь квадратный корень из числа 432.
Число 432 принадлежит промежутку [100; 10000]. Значит квадратный корень следует искать в промежутке [10; 100]. Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо.
Извлечем квадратный корень из числа 432 с точностью до десятых.
В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.
Проверим, например, число 20,8. Для этого возведём его в квадрат:
20,82 = 432,64
Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432. Проверим тогда значение 20,7
20,72 = 428,49
Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49, которое меньше исходного числа 432, но близко к нему. Значит √432 ≈ 20,7.
Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.
Например, извлечём корень из числа 4225. Нам известен ближайший меньший квадрат 3600, и ближайший больший квадрат 4900
3600 < 4225 < 4900
Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:
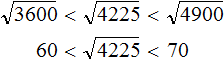
Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70. Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900. Затем можно проверить, например, корень 64. Возведём его в квадрат (или умнóжим данное число само на себя)
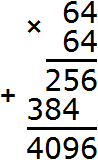
Корень 64 не годится. Проверим корень 65
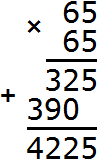
Получается 4225. Значит 65 является корнем числа 4225
![]()
Тождественные преобразования с квадратными корнями
Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.
Квадратный корень из произведения
Квадратный корень из произведения это выражение вида ![]() , где a и b некоторые числа.
, где a и b некоторые числа.
Например, выражение ![]() является квадратным корнем из произведения чисел 4 и 9.
является квадратным корнем из произведения чисел 4 и 9.
Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение ![]() в виде произведения корней
в виде произведения корней ![]() . Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6
. Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6
![]()
Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9, которое равно 36. Затем извлечь квадратный корень из числа 36
![]()
Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.
Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12
![]()
Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.
Итак, разлóжим число 144 на простые множители:

Получили следующее разложение:
![]()
В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.
Тогда четыре двойки можно заменить на запись 22 × 22, а две тройки заменить на 32
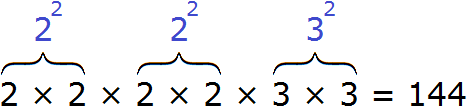
В результате будем иметь следующее разложение:
![]()
Теперь можно извлекáть квадратный корень из разложения числа 144
![]()
Применим правило извлечения квадратного корня из произведения:
![]()
Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.
Тогда получится произведение 2 × 2 × 3, которое равно 12
![]()
Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.
Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3. Это разложение можно записать под кóрнем как есть:
![]()
затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:
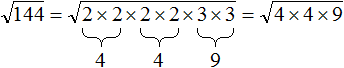
Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:
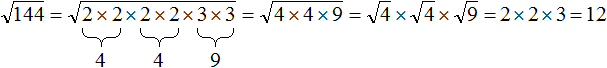
С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.
Например, извлечём квадратный корень из числа 13456. Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.
Итак, разложим число 13456 на простые множители:

В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 22. А два числа 29 предстáвим как 292. В результате полýчим следующее разложение числа 13456
![]()
Теперь будем извлекать квадратный корень из разложения числа 13456
![]()
Итак, если a ≥ 0 и b ≥ 0, то ![]() . То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
. То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Докажем равенство ![]() . Для этого воспользуемся определением квадратного корня.
. Для этого воспользуемся определением квадратного корня.
Согласно определению, квадратным корня из числа a есть число b, при котором выполняется равенство b2 = a.
В нашем случае нужно удостовериться, что правая часть равенства ![]() при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.
при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.
Итак, выпишем правую часть равенства ![]() и возведём ее во вторую степень:
и возведём ее во вторую степень:
![]()
Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:
![]()
Ранее было сказано, что если выражение вида ![]() возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня
возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня ![]()
![]()
Значит равенство ![]() справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.
справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.
Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:
![]() , при a ≥ 0 и b ≥ 0, c ≥ 0.
, при a ≥ 0 и b ≥ 0, c ≥ 0.
Пример 1. Найти значение квадратного корня ![]()
Запишем корень ![]() в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
![]()
Пример 2. Найти значение квадратного корня ![]()
Предстáвим число 250 в виде произведения чисел 25 и 10. Делать это будем под знáком корня:
![]()
Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100
![]()
Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:
![]()
Пример 3. Найти значение квадратного корня ![]()
Воспользуемся правилом возведения степени в степень. Степень 114 предстáвим как (112)2.
![]()
Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:
![]()
В нашем случае квадратный корень из числа (112)2 будет равен 112. Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется:
![]()
Далее возводим число 11 во вторую степень и получаем окончательный ответ:
![]()
Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 114 нужно записать в виде произведения 112 × 112. Затем извлечь квадратный корень из этого произведения:
![]()
Пример 4. Найти значение квадратного корня ![]()
Перепишем степень 34 в виде (32)2, а степень 56 в виде (53)2
![]()
Далее используем правило извлечения квадратного кóрня из произведения:
![]()
Далее используем правило извлечения квадратного кóрня из квадрата числа:
![]()
Вычислим произведение получившихся степеней и полýчим окончательный ответ:
![]()
Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения ![]()
Запишем корень ![]() в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
![]()
Пример 6. Найти значение квадратного корня ![]()
![]()
Пример 7. Найти значение квадратного корня ![]()
![]()
Если первый сомножитель умножить на число n, а второй сомножитель разделить на это число n, то произведение не изменится.
Например, произведение 8 × 4 равно 32
8 × 4 = 32
Умнóжим сомножитель 8 скажем на число 2, а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2, которое тоже равно 32.
(8 × 2) × (4 : 2) = 32
Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.
Например, извлечём квадратный корень из произведения ![]() . Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
. Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
Проанализировав подкореннóе выражение 1,6 × 90, можно заметить, что если первый сомножитель 1,6 умножить на 10, а второй сомножитель 90 разделить на 10, то полýчится произведение 16 × 9. Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения.
Запишем полное решение данного примера:
![]()
Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:
![]()
Пример 9. Найти значение квадратного корня ![]()
Умнóжим первый сомножитель на 10, а второй раздéлим на 10. Тогда под кóрнем образуется произведение 36 × 0,04, квадратный корень из которого извлекается:
![]()
Если в равенстве ![]() поменять местами левую и правую часть, то полýчим равенство
поменять местами левую и правую часть, то полýчим равенство ![]() . Это преобразовáние позволяет упрощáть вычисление некоторых корней.
. Это преобразовáние позволяет упрощáть вычисление некоторых корней.
Например, узнáем чему равно значение выражения ![]() .
.
Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом ![]() , то есть заменим выражение из двух корней
, то есть заменим выражение из двух корней ![]() на выражение с одним корнем, под которым будет произведение из чисел 10 и 40
на выражение с одним корнем, под которым будет произведение из чисел 10 и 40
![]()
Теперь найдём значение произведения, находящегося под корнем:
![]()
А квадратный корень из числа 400 извлекается. Он равен 20
![]()
Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.
Например, найдём значение выражения ![]() .
.
Воспользуемся правилом ![]()
![]()
Сомножитель 32 это 25. Предстáвим этот сомножитель как 2 × 24
![]()
Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 24 предстáвим в виде степени с показателем 2
![]()
Теперь воспóльзуемся правилом ![]() и вычислим окончательный ответ:
и вычислим окончательный ответ:
![]()
Пример 12. Найти значение выражения ![]()
Воспользуемся правилом ![]()
![]()
Сомножитель 8 это 2 × 2 × 2, а сомножитель 98 это 2 × 7 × 7
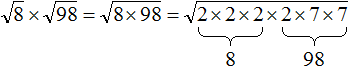
Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 22 × 22, а две семёрки как 72
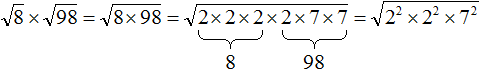
Теперь воспользуемся правилом ![]() и вычислим окончательный ответ:
и вычислим окончательный ответ:
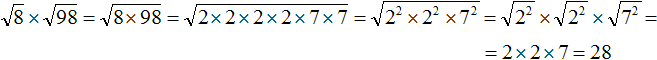
Квадратный корень из дроби
Квадратный корень вида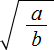 равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b
равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b

Например, квадратный корень из дроби ![]() равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9
равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9
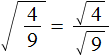
Вычислим квадратные корни в числителе и знаменателе:
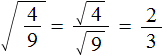
Значит, квадратный корень из дроби ![]() равен
равен .
Докáжем, что равенство  является верным.
является верным.
Возведём правую часть во вторую степень. Если в результате полýчим дробь ![]() , то это будет означать, что равенство
, то это будет означать, что равенство  верно:
верно:
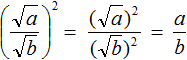
Пример 1. Извлечь квадратный корень 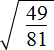
Воспользуемся правилом извлечения квадратного корня из дроби:
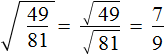
Пример 2. Извлечь квадратный корень 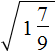
Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:
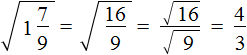
Пример 3. Извлечь квадратный корень ![]()
Квадратным корнем из числа 0,09 является 0,3. Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби.
Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:
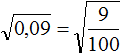
Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:
Пример 4. Найти значение выражения ![]()
Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:
![]()
Также можно воспользоваться правилом извлечения квадратного корня из дроби:
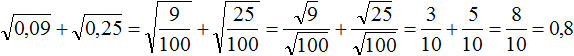
В данном примере первый способ оказался проще и удобнее.
Пример 5. Найти значение выражения ![]()
Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4
![]()
Пример 6. Найти значение выражения ![]()
Сначала найдём значение квадратного корня ![]() . Он равен 0,6 поскольку 0,62 = 0,36
. Он равен 0,6 поскольку 0,62 = 0,36
![]()
Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:
![]()
Вынесение множителя из-под знака корня
В некоторых задачах может быть полезным вынесение множителя из-под знака корня.
Рассмотрим квадратный корень из произведения ![]() . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
. Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
![]()
В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение ![]() оставим без изменений:
оставим без изменений:
![]()
Это и есть вынесение множителя из-под знака корня.
На практике подкореннóе выражение чаще всего требуется разложить на множители.
Пример 2. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:
![]()
Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:
![]()
Пример 3. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:
![]()
Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:
![]()
Пример 4. Вынести множитель из-под знака корня в выражении ![]()
Воспользуемся правилом извлечения квадратного корня из произведения:
![]()
Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:
![]()
Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √15 и 11 местами:
![]()
Пример 5. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 4 и 3
![]()
Воспользуемся правилом извлечения квадратного корня из произведения:
![]()
Извлечём корень из числа 4, а выражение √3 остáвим без изменений:
![]()
Пример 6. Упростить выражение ![]()
Предстáвим второе слагаемое ![]() в виде
в виде ![]() . А третье слагаемое
. А третье слагаемое ![]() предстáвим в виде
предстáвим в виде ![]()
![]()
Теперь в выражениях ![]() и
и ![]() вынесем множитель из-под знака корня:
вынесем множитель из-под знака корня:
![]()
Во втором слагаемом ![]() перемнóжим числа −4 и 4. Остальное перепишем без изменений:
перемнóжим числа −4 и 4. Остальное перепишем без изменений:
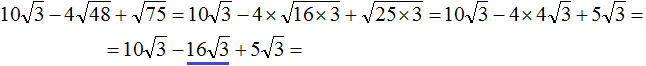
Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:
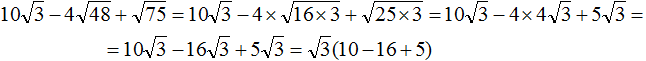
Вычислим содержимое скобок, полýчим −1
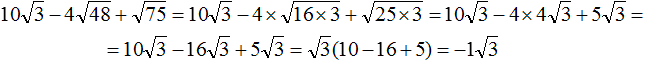
Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3
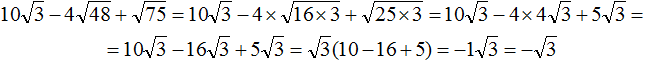
Внесение множителя под знак корня
Рассмотрим следующее выражение:
![]()
В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.
Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.
Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15
![]()
Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.
Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:
![]()
Итак, если данó выражение ![]() , и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
, и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
![]()
Пример 1. Внести множитель под знак корня в выражении ![]()
Возведём число 7 во вторую степень и внесём его под знак корня:
![]()
Пример 2. Внести множитель под знак корня в выражении ![]()
Возведём число 10 во вторую степень и внесем его под знак корня:
![]()
Пример 3. Внести множитель под знак корня в выражении ![]()
![]()
Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида ![]() не имеет смысла.
не имеет смысла.
Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.
Пример 4. Внести множитель по знак корня в выражении ![]()
В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:
![]()
Пример 5. Выполнить возведéние в степень в следующем выражении:
![]()
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Роль переменной a в данном случае играет выражение √3, роль переменной b — выражение √2. Тогда полýчим:
![]()
Теперь необходимо упростить получившееся выражение.
Для выражений ![]() и
и ![]() применим правило
применим правило ![]() . Ранее мы говорили, что если выражение вида
. Ранее мы говорили, что если выражение вида ![]() возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.
возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.
А в выражении ![]() для множителей
для множителей ![]() и
и ![]() применим правило
применим правило ![]() . То есть заменим произведение корней на один общий корень:
. То есть заменим произведение корней на один общий корень:
![]()
Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом ![]() вычислить произведение, которое под кóрнем:
вычислить произведение, которое под кóрнем:
![]()
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Тождественные преобразования многочленов
Возведение двучлена в степень
Двучлен — это многочлен, состоящий из двух членов. В прошлых уроках мы возводили двучлен во вторую и третью степень, тем самым получили формулы сокращенного умножения:
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Но двучлен можно возводить не только во вторую и третью степень, но и в четвёртую, пятую или более высокую степень.
К примеру, возведём двучлен a + b в четвертую степень:
(a + b)4
Представим это выражение в виде произведения двучлена a + b и куба этого же двучлена
(a + b)(a + b)3
Сомножитель (a + b)3 можно заменить на правую часть формулы куба суммы двух выражений. Тогда получим:
(a + b)(a3 + 3a2b + 3ab2 + b3)
А это обычное перемножение многочленов. Выполним его:
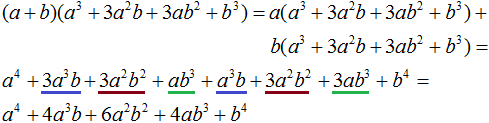
То есть при возведении двучлена a + b в четвертую степень получается многочлен a4 + 4a3b + 6a2b2 + 4ab3 + b4
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Возведение двучлена a + b в четвертую степень можно выполнить ещё и так: представить выражение (a + b)4 в виде произведения степеней (a + b)2(a + b)2
(a + b)2(a + b)2
Но выражение (a + b)2 равно a2 + 2ab + b2. Заменим в выражении (a + b)2(a + b)2 квадраты суммы на многочлен a2 + 2ab + b2
(a2 + 2ab + b2)(a2 + 2ab + b2)
А это опять же обычное перемножение многочленов. Выполним его. У нас получится тот же результат, что и раньше:
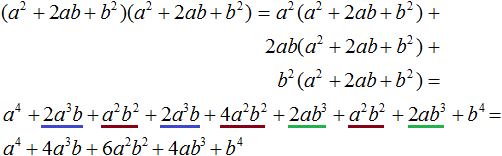
Возведение трёхчлена в степень
Трёхчлен — это многочлен, состоящий из трёх членов. Например, выражение a + b + c является трёхчленом.
Иногда может возникнуть задача возвести трёхчлен в степень. Например, возведём в квадрат трехчлен a + b + c
(a + b + c)2
Два члена внутри скобок можно заключить в скобки. К примеру, заключим сумму a + b в скобки:
((a + b) + c)2
В этом случае сумма a + b будет рассматриваться как один член. Тогда получается, что в квадрат мы возводим не трёхчлен, а двучлен. Сумма a + b будет первым членом, а член c — вторым членом. А как возводить в квадрат двучлен мы уже знаем. Для этого можно воспользоваться формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Применим эту формулу к нашему примеру:
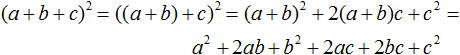
Таким же способом можно возвести в квадрат многочлен, состоящий из четырёх и более членов. Например, возведем в квадрат многочлен a + b + c + d
(a + b + c + d)2
Представим многочлен в виде суммы двух выражений: a + b и c + d. Для этого заключим их в скобки:
((a + b) + (c + d))2
Теперь воспользуемся формулой квадрата суммы двух выражений:
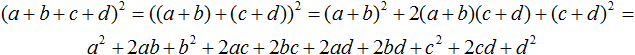
Выделение полного квадрата из квадратного трёхчлена
Ещё одно тождественное преобразование, которое может пригодиться при решении задач это выделение полного квадрата из квадратного трёхчлена.
Квадратным трехчленом называют трёхчлен второй степени. Например, следующие трехчлены являются квадратными:
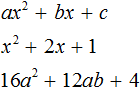
Идея выделения полного квадрата из таких трехчленов заключается в том, чтобы представить исходный квадратный трехчлен в виде выражения (a + b)2 + c, где (a + b)2 полный квадрат, а c — некоторое числовое или буквенное выражение.
Например, выделим полный квадрат из трёхчлена 4x2 + 16x + 19.
Для начала нужно построить выражение вида a2 + 2ab + b2. Строить мы его будем из трехчлена 4x2 + 16x + 19. Для начала определимся какие члены будут играть роли переменных a и b
Роль переменной a будет играть член 2x, поскольку первый член трехчлена 4x2 + 16x + 19, а именно 4x2 получается если 2x возвести в квадрат:
(2x)2 = 4x2
Итак, переменная a равна 2x
a = 2x
Теперь возвращаемся к исходному трёхчлену и сразу обращаем внимание на выражение 16x. Это выражение является удвоенным произведением первого выражения a (в нашем случае это 2x) и второго пока неизвестного нам выражения b. Временно поставим на его место вопросительный знак:
2 × 2x × ? = 16x
Если внимательно посмотреть на выражение 2 × 2x × ? = 16x, то интуитивно станет понятно, что членом b в данной ситуации является число 4, поскольку выражение 2 × 2x равно 4x, и чтобы получить 16x нужно домножить 4x на 4.
2 × 2x × 4 = 16x
Отсюда делаем вывод, что переменная b равна 4
b = 4
Значит, нашим полным квадратом будет выражение (2x)2 + 2 × 2x × 4 + 42
Теперь у нас всё готово для выделения полного квадрата из трёхчлена 4x2 + 16x + 19.
Итак, возвратимся к исходному трехчлену 4x2 + 16x + 19 и попробуем аккуратно внедрить в него полученный нами полный квадрат (2x)2 + 2 × 2x × 4 + 42
4x2 + 16x + 19 =
Вместо 4x2 записываем (2x)2
4x2 + 16x + 19 = (2x)2
Далее вместо 16x записываем удвоенное произведение, а именно 2 × 2x × 4
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4
Далее прибавляем квадрат второго выражения:
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42
А член 19 пока переписываем как есть:
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42 + 19
Теперь обратим внимание на то, что полученный нами многочлен (2x)2 + 2 × 2x × 4 + 42 + 19 не тождественен изначальному трёхчлену 4x2 + 16x + 19. Убедиться в этом можно приведя многочлен (2x)2 + 2 × 2x × 4 + 42 + 19 к стандартному виду:
(2x)2 + 2 × 2x × 4 + 42 + 19 = 4x2 + 16x + 42 + 19
Видим, что получается многочлен 4x2 + 16x + 42 + 19, а должен был получиться 4x2 + 16x + 19. Это по причине того, что член 42 был искусственно внедрён в изначальный трёхчлен с целью организовать полный квадрата из трёхчлена 4x2 + 16x + 19.
Чтобы сохранить значение исходного многочлена, нужно после прибавления члена 42 сразу же вычесть его
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42 − 42 + 19
Теперь выражение (2x)2 + 2 × 2x × 4 + 42 можно свернуть, то есть записать в виде (a + b)2. В нашем случае получится выражение (2x + 4)2
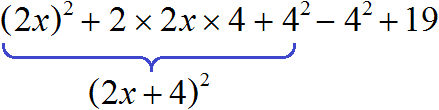
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42 − 42 + 19 = (2x + 4)2 − 42 + 19
Оставшиеся члены −42 и 19 можно сложить. −42 это −16, отсюда −16 + 19 = 3
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42 − 42 + 19 = (2x + 4)2 − 42 + 19 = (2x + 4)2 + 3
Значит, 4x2 + 16x + 19 = (2x + 4)2 + 3
Пример 2. Выделить полный квадрат из квадратного трёхчлена x2 + 2x + 2
Сначала построим выражение вида a2 +2ab + b2. Роль переменной a в данном случае играет x, поскольку x2 = x2.
Следующий член исходного трёхчлена 2x перепишем в виде удвоенного произведение первого выражения (это у нас x) и второго выражения b (это будет 1).
2 × x × 1 = 2x
Если b = 1, то полным квадратом будет выражение x2 + 2x + 12.
Теперь вернёмся к исходному квадратному трёхчлену и внедрим в него полный квадрата x2 + 2x + 12
x2 + 2x + 2 = x2 + 2x + 12 − 12 + 2 = (x + 1)2 + 1
Как и в прошлом примере член b (в данном примере это 1) после прибавления сразу был вычтен с целью сохранения значения исходного трёхчлена.
Рассмотрим следующее числовое выражение:
9 + 6 + 2
Значение этого выражения равно 17
9 + 6 + 2 = 17
Попробуем выделить в этом числовом выражении полный квадрат. Для этого сначала построим выражение вида a2 + 2ab + b2. Роль переменной a в данном случае играет число 3, поскольку первый член выражения 9 + 6 + 2, а именно 9 можно представить как 32.
Второй член 6 представим в виде удвоенного произведения первого члена 3 и второго 1
2 × 3 × 1 = 6
То есть переменная b будет равна единице. Тогда полным квадратом будет выражение 32 + 2 × 3 × 1 + 12. Внедрим его в исходное выражение:
32 + 6 + 2 = 32 + 2 × 3 × 1 + 12 − 12 + 2
Свернем полный квадрат, а члены −12 и 2 слóжим:
32 + 6 + 2 = 32 + 2 × 3 × 1 + 12 − 12 + 2 = (3 + 1)2 + 1
Получилось выражение (3 + 1)2 + 1, которое по прежнему равно 17
(3 + 1)2+1 = 42 + 1 = 17
Допустим, у нас имеются квадрат и два прямоугольника. Квадрат со стороной 3 см, прямоугольник со сторонами 2 см и 3 см, а также прямоугольник со сторонами 1 см и 2 см
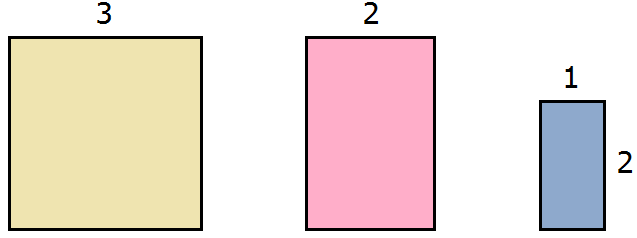
Вычислим площадь каждой фигуры. Площадь квадрата будет составлять 32 = 9 см2, площадь розового прямоугольника — 2 × 3 = 6 см2, площадь сиреневого — 1 × 2 = 2 см2
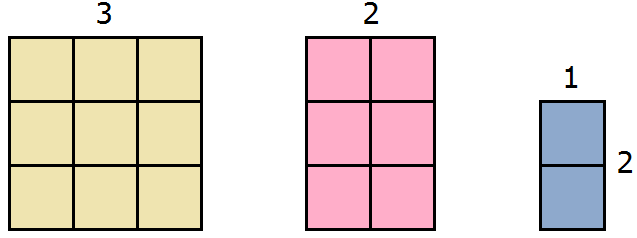
Запишем сумму площадей этих прямоугольников:
9 + 6 + 2
Это выражение можно понимать как объединение квадрата и двух прямоугольников в единую фигуру:
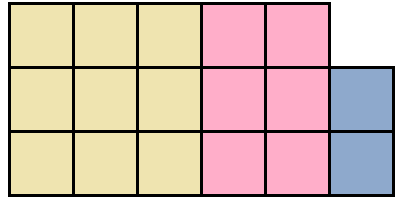
Тогда получается фигура, площадь которой 17 см2. Действительно, в представленной фигуре содержится 17 квадратов со стороной 1 см.
Попробуем из имеющейся фигуры образовать квадрат. Причем максимально большой квадрат. Для этого будем использовать части от розового и сиреневого прямоугольника.
Чтобы образовать максимально большой квадрат из имеющейся фигуры, можно желтый квадрат оставить без изменений, а половину от розового прямоугольника прикрепить к нижней части желтого квадрата:
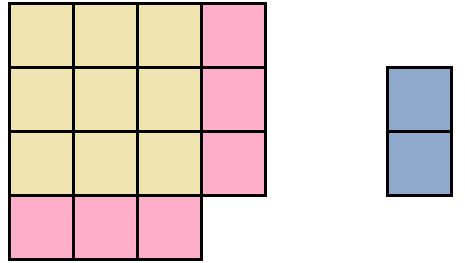
Видим, что до образования полного квадрата не хватает еще одного квадратного сантиметра. Его мы можем взять от сиреневого прямоугольника. Итак, возьмем один квадрат от сиреневого прямоугольника и прикрепим его к образуемому большому квадрату:
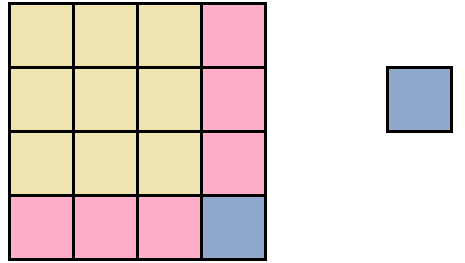
Теперь внимательно посмотрим к чему мы пришли. А именно на желтую часть фигуры и розовую часть, которая по сути увеличила прежний жёлтый квадрат. Не означает ли это то, что была сторона квадрата равная 3 см, и эта сторона была увеличена на 1 см, что привело в итоге к увеличению площади?
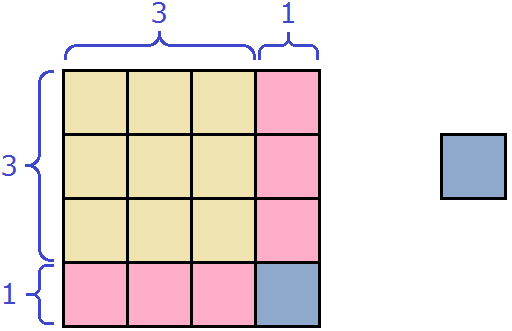
(3 + 1)2
Выражение (3 + 1)2 равно 16, поскольку 3 + 1 = 4, а 42 = 16. Этот же результат можно получить, если воспользоваться формулой квадрата суммы двух выражений:
(3 + 1)2 = 32 + 6 + 1 = 9 + 6 + 1 = 16
Действительно, в образовавшемся квадрате содержится 16 квадратов.
Оставшийся один квадратик от сиреневого прямоугольника можно прикрепить к образовавшемуся большому квадрату. Ведь речь изначально шла о единой фигуре:
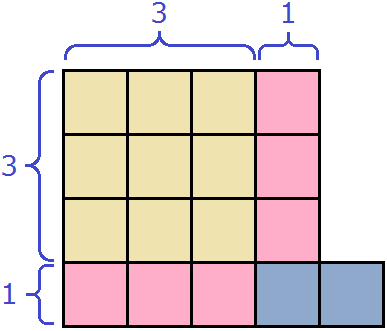
(3 + 1)2 + 1
Прикрепление маленького квадратика к имеющемуся большому квадрату описывается выражением (3 + 1)2 + 1. А это есть выделение полного квадрата из выражения 9 + 6 + 2
9 + 6 + 2 = 32 + 6 + 2 = 32 + 2 × 3 × 1 + 12 − 12 + 2 = (3 + 1)2 + 1
Выражение (3 + 1)2 + 1, как и выражение 9 + 6 + 2 равно 17. Действительно, площадь образовавшейся фигуры равна 17 см2.
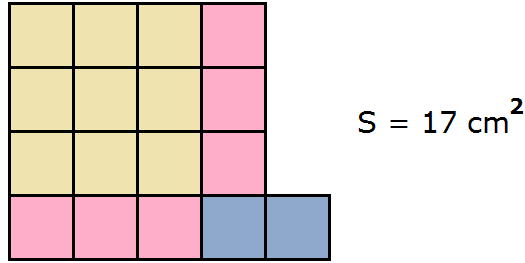
Пример 4. Выполним выделение полного квадрата из квадратного трёхчлена x2 + 6x + 8
x2 + 6x + 8 = x2 + 2 × x × 3 + 32 − 32 + 8 = (x + 3)2 − 1
В некоторых примерах при построении выражения a2 + 2ab + b2 не бывает возможным сразу определить значения переменных a и b.
Например, выполним выделение полного квадрата из квадратного трёхчлена x2 + 3x + 2
Переменной a соответствует x. Второй член 3x нельзя представить в виде удвоенного произведения первого выражения и второго. В этом случае второй член следует умножить на 2, и чтобы значение исходного многочлена не изменилось, сразу же выполнить деление на 2. Выглядеть это будет так:
![]()
Получившаяся дробь ![]() и содержит значения переменных a и b. Наша задача суметь правильно их распознать. Перепишем эту дробь в виде произведения множителя 2, дроби
и содержит значения переменных a и b. Наша задача суметь правильно их распознать. Перепишем эту дробь в виде произведения множителя 2, дроби ![]() и переменной x
и переменной x
![]()
Теперь второй член представлен в виде удвоенного произведения первого выражения и второго. Переменная a, как было сказано ранее, равна x. А переменная b равна дроби ![]()
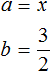
Возвращаемся к нашему примеру и прибавляем квадрат второго выражения, и чтобы значение выражения не изменилось, сразу же вычитаем его:
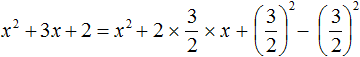
Прибавляем оставшийся член 2
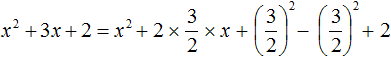
Свернём полный квадрат:
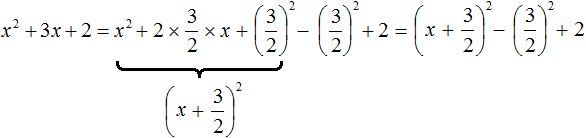
Оставшийся квадрат второго выражения и число 2 можно сложить. В итоге получим:
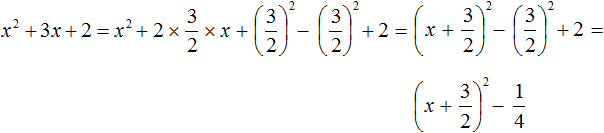
Пример 6. Выполним выделение полного квадрата из квадратного трёхчлена 9x2 + 18x + 7
![]()
Пример 7. Выполним выделение полного квадрата из квадратного трёхчлена x2 − 10x + 1
В данном трёхчлене первые два члена связаны знаком «минус». В этом случае как и раньше нужно выделить полный квадрат, но это будет квадрат разности. Проще говоря, нужно построить выражение вида a2 − 2ab + b2.
![]()
Пример 8. Выполним выделение полного квадрата из квадратного трёхчлена 16x2 + 4x + 1
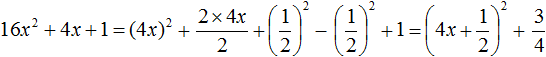
Пример 9. Разложить многочлен x2 + 6x + 8 на множители при помощи выделения полного квадрата.
Сначала выделим полный квадрат:
![]()
Получившийся многочлена (x + 3)2 − 1 является разностью квадратов, поскольку единица может быть представлена в виде 12. Воспользуемся формулой разности квадратов и разложим многочлен (x + 3)2 − 1 на множители:
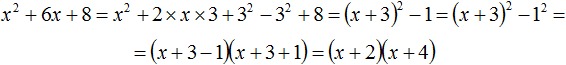
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Деление многочленов
Продолжаем изучать многочлены. В данном уроке мы научимся их делить.
Деление многочлена на одночлен
Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.
Например, разделим многочлен 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Запишем это деление в виде дроби:
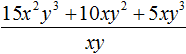
Теперь делим каждый член многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Получающиеся частные будем складывать:
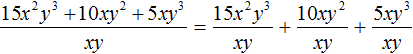
Получили привычное для нас деление одночленов. Выполним это деление:
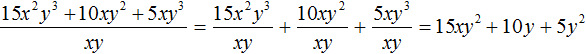 Таким образом, при делении многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy получается многочлен 15xy2 + 10y + 5y2.
Таким образом, при делении многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy получается многочлен 15xy2 + 10y + 5y2.
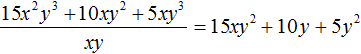
При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.
В нашем примере произведение полученного многочлена 15xy2 + 10y + 5y2 и делителя xy должно быть равно многочлену 15x2y3 + 10xy2 + 5xy3, то есть исходному делимому. Проверим так ли это:
(15xy2 + 10y + 5y2)xy = 15x2y3 + 10xy2 + 5xy3
Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.
Например, чтобы сложить дроби ![]() ,
, ![]() и
и нужно записать следующее выражение:
![]()
Если мы вычислим выражение ![]() , то получим дробь
, то получим дробь ![]() , значение которой равно 1,5.
, значение которой равно 1,5.
При этом выражение ![]() мы можем вернуть в исходное состояние
мы можем вернуть в исходное состояние ![]() , и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5
, и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5
![]()
Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x, образуется три дроби с общим знаменателем x
![]()
Вычисление каждой дроби даст в результате многочлен a + b + c
![]()
Пример 2. Разделить многочлен 8m3n + 24m2n2 на одночлен 8m2n
![]()
Пример 3. Разделить многочлен 4c2d − 12c4d3 на одночлен −4c2d
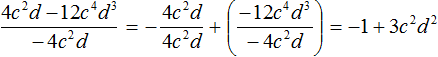
Деление одночлена на многочлен
Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.
Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5.
![]()
Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy. Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy, поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.
Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.
Например, найдём значение выражения ![]() при x = 2.
при x = 2.
Выражение ![]() представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования. Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:
представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования. Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:
![]()
Деление многочлена на многочлен
Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3, получается многочлен x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
(x + 5)(x + 3) = x2 + 8x + 15
Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.
Тогда согласно этому правилу, деление полученного нами многочлена x2 + 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5.
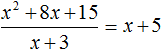
Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.
Выполним уголком деление многочлена x2 + 8x + 15 на многочлен x + 3. Так мы поэтапно увидим, как получается многочлен x + 5.
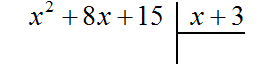
В данном случае результат нам известен заранее. Это будет многочлен x + 5. Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.
Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.
Сейчас наша задача найти первый член нового многочлена. Как это сделать?
Когда мы изначально перемножали многочлены x + 5 и x + 3, мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:
![]()
Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.
Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.
Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.
Если первый член делимого (в нашем случае это x2) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:
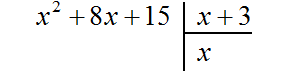
Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3. На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3, получается x2 + 3x. Записываем этот многочлен под делимым x2+ 8x+ 15 так, чтобы подобные члены располагались друг под другом:
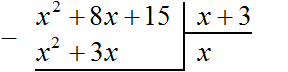
Теперь из делимого x2 + 8x + 15 вычитаем x2 + 3x. Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
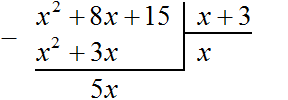
Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:
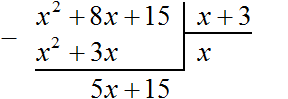
Теперь делим многочлен 5x + 15 на x + 3. Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x) разделить на первый член делителя (это член x). Если 5x разделить на x, получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)
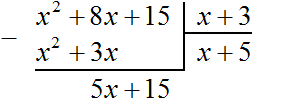
Теперь умножаем 5 на делитель x + 3. При умножении 5 на x + 3, получается 5x + 15. Записываем этот многочлен под делимым 5x + 15
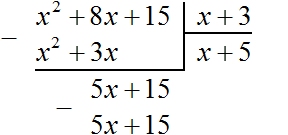
Теперь из делимого 5x + 15 вычитаем 5x + 15. Если из 5x + 15 вычесть 5x + 15 получится 0.
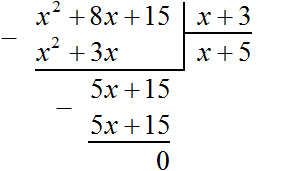
На этом деление завершено.
После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3, должен получаться многочлен x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
Пример 2. Разделить многочлен x2 − 8x + 7 на многочлен x − 7
Записываем уголком данное деление:
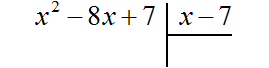
Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x. Записываем x под правым углом:
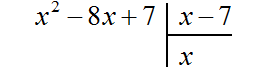
Умножаем x на x − 7, получаем x2 − 7x. Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
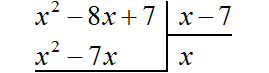
Вычитаем из x2 − 8x + 7 многочлен x2 − 7x. При вычитании x2 из x2 получается 0. Ноль не записываем. А при вычитании −7x из −8x получается −x, поскольку −8x − (−7x) = −8x + 7x = −x. Записываем −x под членами −7x и −8x. Далее сносим следующий член 7
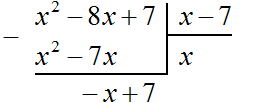
Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:
![]()
Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7. Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x) разделить на первый член делителя (это член x). Если −x разделить на x, получится −1. Записываем −1 под правым углом вместе со своим знаком:
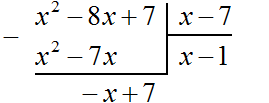
Умножаем −1 на x − 7, получаем −x + 7. Записываем этот многочлен под делимым −x + 7
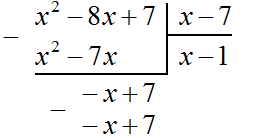
Теперь из −x + 7 вычитаем −x + 7. Если из −x + 7 вычесть −x + 7 получится 0
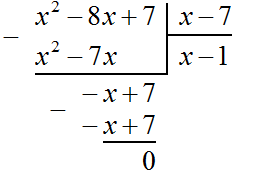
Деление завершено. Таким образом, частное от деления многочлена x2 − 8x + 7 на многочлен x − 7 равно x − 1
![]()
Выполним проверку. Умножим частное x − 1 на делитель x − 7. У нас должен получиться многочлен x2 − 8x + 7
(x − 1)(x − 7) = x2 − x − 7x + 7 = x2 − 8x + 7
Пример 3. Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3
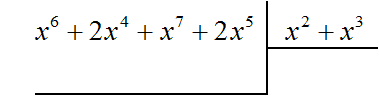
Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x4
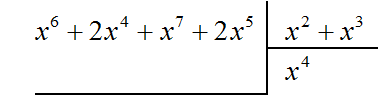
Умножаем x4 на делитель x2 + x3 и полученный результат записываем под делимым. Если x4 умножить на x2 + x3 получится x6 + x7. Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:
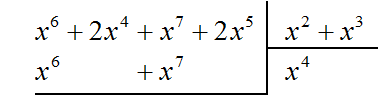
Теперь из делимого вычитаем многочлен x6 + x7. Вычитание x6 из x6 даст в результате 0. Вычитание x7 из x7 тоже даст в результате 0. Оставшиеся члены 2x4 и 2x5 снесём:
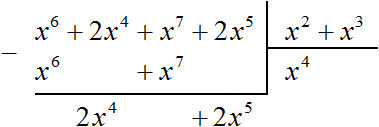
Получилось новое делимое 2x4 + 2x5. Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7
![]()
Разделим многочлен 2x4 + 2x5 на делитель x2 + x3. Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x2. Записываем этот член в частном:
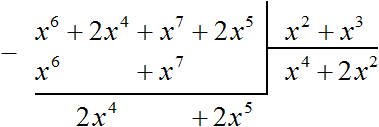
Умножаем 2x2 на делитель x2 + x3 и полученный результат записываем под делимым. Если 2x2 умножить на x2 + x3 получится 2x4 + 2x5. Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:
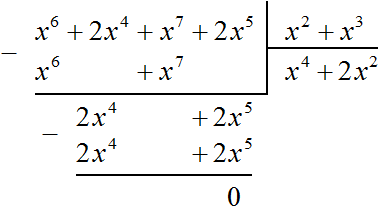
Вычитание многочлена 2x4 + 2x5 из многочлена 2x4 + 2x5 дало в результате 0, поэтому деление успешно завершилось.
В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.
Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.
Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x6 + 2x4 + x7 + 2x5 упорядочить в порядке убывания степеней, то получим многочлен x7 + x6 + 2x5 + 2x4. А если члены многочлена x2 + x3 упорядочить в порядке убывания степеней, то получим многочлен x3 + x2
Тогда деление уголком многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 примет следующий вид:
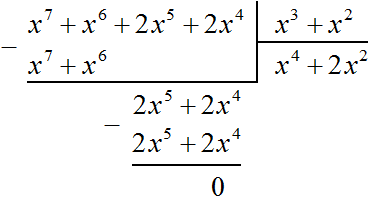
Деление завершено. Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2
![]()
Выполним проверку. Умножим частное x4 + 2x2 на делитель x2 + x3. У нас должен получиться многочлен x6 + 2x4 + x7 + 2x5
(x4 + 2x2)(x2 + x3) = x4 (x2 + x3) + 2x2(x2 + x3) = x6 + 2x4 + x7 + 2x5
При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.
Перепишем умножение (x4 + 2x2)(x2 + x3) упорядочив члены многочленов в порядке убывания степеней.
(x4 + 2x2)(x3 + x2) = x4(x3 + x2) + 2x2(x3 + x2) = x7 + x6 + 2x5 + 2x4
Пример 4. Разделить многочлен 17x2 − 6x4 + 5x3 − 23x + 7 на многочлен 7 − 3x2 − 2x
Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:
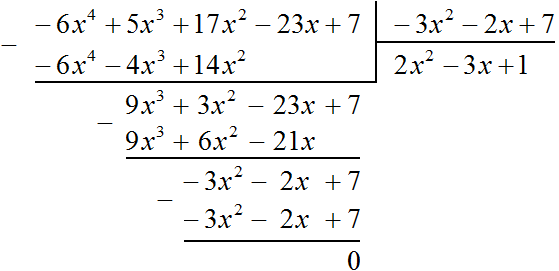
Значит,
![]()
Пример 5. Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2
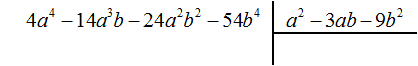
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a2. Записываем 4a2 в частном:
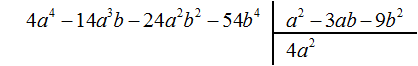
Умножим 4a2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым:
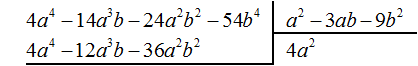
Вычтем из делимого полученный многочлен 4a4 − 12a3b − 36a2b2
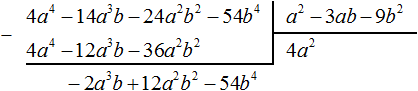
Теперь делим −2a3b + 12a2b2 − 54b4 на делитель a2 − 3ab − 9b2. Разделим первый член делимого на первый член делителя, получим −2ab. Записываем −2ab в частном:
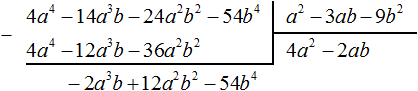
Умножим −2ab на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым −2a3b + 12a2b2 − 54b4
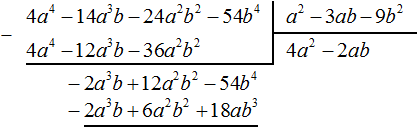
Вычтем из многочлена −2a3b + 12a2b2 − 54b4 многочлен −2a3b + 12a2b2 − 18ab3. При вычитании подобных членов обнаруживаем, что члены −54b4 и 18ab3 не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a3b из −2a3b и 6a2b2 из 12a2b2, а вычитание 18ab3 из −54b4 запишем в виде разности −54b4 − (+18ab3) или −54b4 − 18ab3
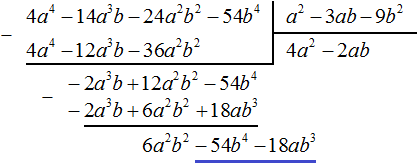
Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:
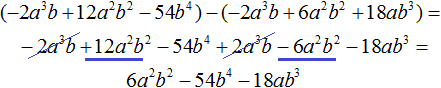
Вернёмся к нашей задаче. Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:
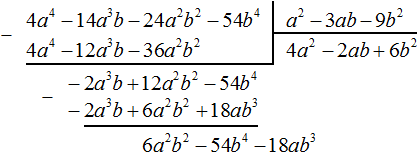
Умножим 6b2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым 6a2b2 − 54b4 − 18ab3. Сразу вычтем этот полученный результат из делимого 6a2b2 − 54b4 − 18ab3
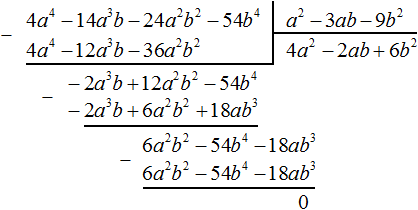
Деление завершено. Таким образом, частное от деления многочлена 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2 равно 4a2 − 2ab + 6b2.
![]()
Выполним проверку. Умножим частное 4a2 − 2ab + 6b2 на делитель a2 − 3ab − 9b2. У нас должен получиться многочлен 4a4 − 14a3b − 24a2b2 − 54b4
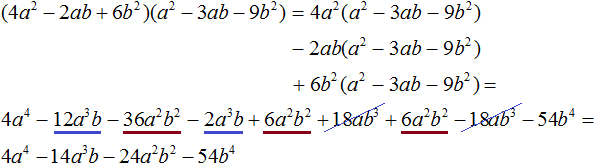
Деление многочлена на многочлен с остатком
Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.
Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:
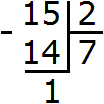
То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:
![]()
Рациональное число ![]() читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.
читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.
Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:
![]()
Например, разделим многочлен 2x3 − x2 − 5x + 4 на многочлен x − 3
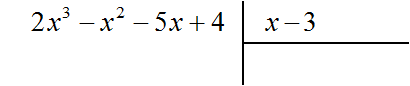
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:
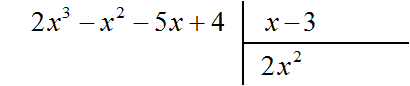
Умножим 2x2 на делитель x − 3 и полученный результат запишем под делимым:
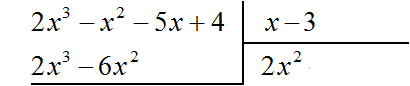
Вычтем из делимого полученный многочлен 2x3 − 6x2
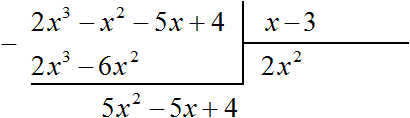
Теперь делим 5x2 − 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:
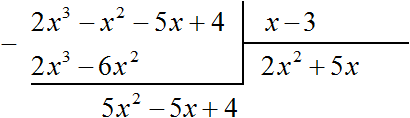
Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x2 − 5x + 4
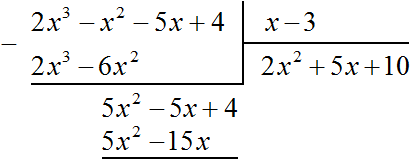
Вычтем из многочлена 5x2 − 5x + 4 многочлен 5x2 − 15x
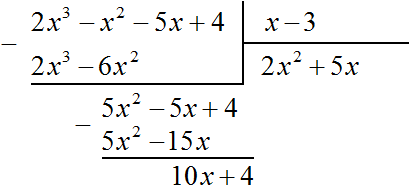
Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:
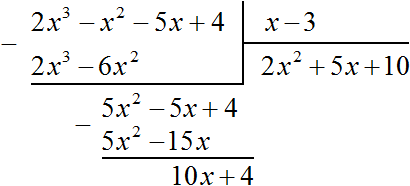
Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4
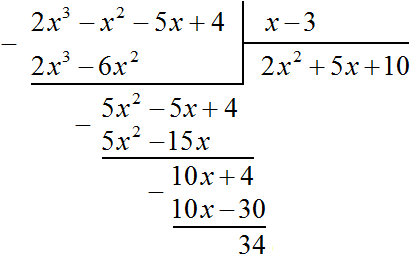
Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.
Поэтому при делении многочлена 2x3 − 2x2 − 5x + 4 на многочлен x − 3 получается 2x2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:
![]()
Когда деление многочленов невозможно
Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.
Например, нельзя разделить многочлен x3 + x на многочлен x4 + x2, поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.
Вопреки этому запрету можно попробовать разделить многочлен x3 + x на многочлен x4 + x2, и даже получить частное x−1, которое при перемножении с делителем будет давать делимое:
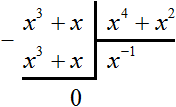
![]()
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x−1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x−1 это дробь ![]() , которая не является произведением.
, которая не является произведением.
Пусть имеется прямоугольник со сторонами 4 и 2
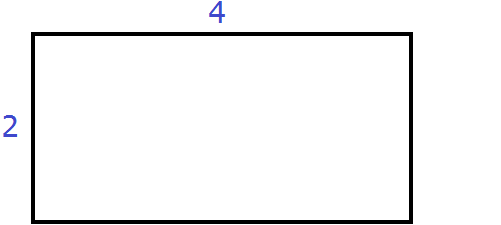
Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.
Увеличим длину и ширину этого прямоугольника на x
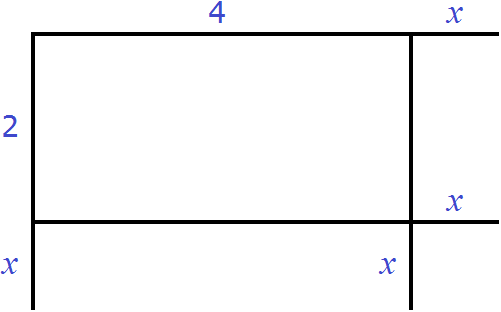
Достроим отсутствующие стороны:
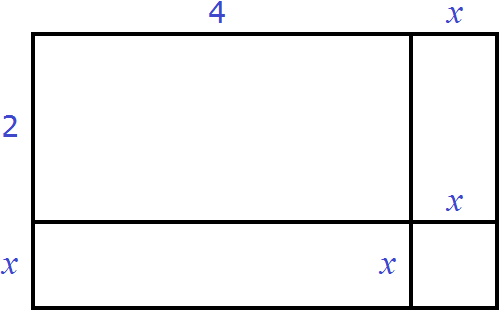
Теперь прямоугольник имеет длину x + 4 и ширину x + 2. Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x2 + 6x + 8
(x + 4)(x + 2) = x2 + 4x + 2x + 8 = x2 + 6x + 8
При этом мы можем выполнить обратную операцию, а именно разделить площадь x2 + 6x + 8 на ширину x + 2 и получить длину x + 4.
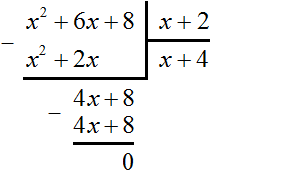
Степень многочлена x2 + 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2, а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Разложение многочлена на множители
Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.
Примером разложения многочлена на множители является вынесение общего множителя за скобки, поскольку исходный многочлен обращается в произведение двух сомножителей, один из которых является одночленом, а другой многочленом.
Разложение многочлена на множители способом вынесения общего множителя за скобки
При вынесении общего множителя за скобки образуется произведение из двух сомножителей, один из которых является одночленом, а другой многочленом. Например:
6x + 3xy = 3x(2 + y)
В рамках изучения многочленов, одночлен принято считать многочленом, состоящим из одного члена. Поэтому, когда в многочлене выносится за скобки общий множитель, то говорят что исходный многочлен представлен в виде произведения многочленов.
В нашем примере многочлен 6x + 3xy был представлен в виде произведения многочленов 3x и (2 + y). По-другому говорят, что многочлен 6x + 3xy разложен на множители 3x и (2 + y)
Существуют также многочлены, в которых можно вынести за скобки такой общий множитель, который является двучленом. Например, рассмотрим многочлен 5a(x + y) + 7a(x + y). В этом многочлене общим множителем является двучлен (x + y). Вынесем его за скобки:
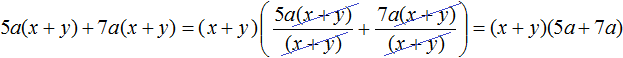
Разложение многочлена на множители способом группировки
Некоторые многочлены содержат группу членов, имеющих общий множитель. Такие группы можно заключать в скобки и далее выносить общий множитель за эти скобки. В результате получается разложение исходного многочлена на множители, которое называют разложением на множители способом группировки.
Рассмотрим следующий многочлен:
ax + ay + 3x + 3y
Члены ax и ay имеют общий множитель a. Выпишем эти члены и заключим их в скобки:
(ax + ay)
Далее в многочлене ax + ay + 3x + 3y члены 3x и 3y имеют общий множитель 3. Выпишем эти члены и тоже заключим их в скобки:
(3x + 3y)
Теперь соединим выражения (ax + ay) и (3x + 3y) знаком «плюс»
(ax + ay) + (3x + 3y)
В многочлене (ax + ay) вынесем за скобки общий множитель a, а в многочлене (3x + 3y) вынесем за скобки общий множитель 3. Делать это нужно в исходном выражении:
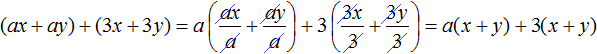
Далее замечаем, что двучлен (x + y) является общим множителем. Вынесем его за скобки. Продолжаем решение в исходном примере. В результате получим:
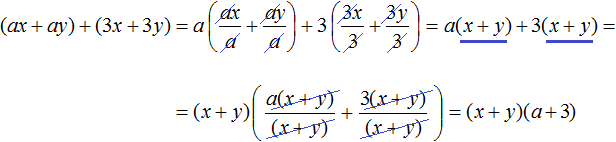
Запишем решение покороче, не расписывая подробно, как каждый член был разделен на общий множитель. Тогда решение получится более компактным:
![]()
Чтобы проверить правильно ли мы разложили многочлен на множители, выполним умножение (x + y)(a + 3). Если мы всё сделали правильно, то получим многочлен ax + ay + 3x + 3y
(x + y)(a + 3) = ax + ay + 3x + 3y
Пример 2. Разложить многочлен 9x + ax − 9y − ay на множители способом группировки.
Члены 9x и −9y имеют общий множитель 9. А члены ax и −ay имеют общий множитель a. Сгруппируем их с помощью скобок, и объединим с помощью знака «плюс»
(9x − 9y) + (ax − ay)
В первой группе (9x − 9y) вынесем за скобки общий множитель 9. Во второй группе (ax − ay) вынесем за скобки за скобки общий множитель a
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y)
Далее вынесем за скобки двучлен (x − y)
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y) = (x − y)(9 + a)
Пример 3. Разложить многочлен ab − 3b + b2 − 3a на множители способом группировки.
Сгруппируем первый член ab с четвёртым членом −3a. А второй член −3b сгруппируем с третьим членом b2. Не забываем, что объединять группы нужно с помощью знака «плюс»
(ab − 3a) + (−3b + b2)
В первой группе вынесем за скобки общий множитель a, во второй группе — общий множитель b
(ab − 3a) + (−3b + b2) = a(b − 3) + b(−3 + b)
Во втором произведении b(−3 + b) в сомножителе (−3 + b) изменим порядок следования членов. Тогда получим b(b − 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3)
Теперь вынесем за скобки общий множитель (b − 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3) = (b − 3)(a + b)
Пример 4. Разложить многочлен x2y + x + xy2 + y + 2xy + 2 на множители способом группировки.
Сгруппируем первый член многочлена со вторым, третий с четвёртым, пятый с шестым:
![]()
В первой группе вынесем за скобки общий множитель x, во второй группе — общий множитель y, в третьей группе — общий множитель 2
![]()
Далее замечаем, что многочлен (xy + 1) является общим множителем. Вынесем его за скобки:
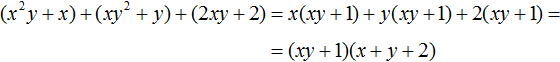
Разложение многочлена на множители по формуле квадрата суммы двух выражений
Формулы сокращённого умножения, которые мы рассматривали в прошлом уроке, можно применять для разложения многочленов на множители.
Вспомним, как выглядит формула квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Поменяем местами левую и правую часть, получим:
a2 + 2ab + b2 = (a + b)2
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)2 представляет собой перемножение двух сомножителей, каждый из которых равен многочлену (a + b).
Стало быть, если нам встретится выражение вида a2 + 2ab + b2, то мы можем представить его в виде произведения (a + b)(a + b). Иными словами, разложить на множители (a + b) и (a + b).
a2 + 2ab + b2 = (a + b)(a + b)
Пример 1. Разложить на множители многочлен 4x2 + 12xy + 9y2
Чтобы воспользоваться формулой a2 + 2ab + b2 = (a + b)2, нужно узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член многочлена 4x2 + 12xy + 9y2 является результатом возведения в квадрат одночлена 2x, поскольку (2x)2 = 4x2. Третий член 9y2 является результатом возведения в квадрат одночлена 3y, поскольку (3y)2 = 9y2, а член 12xy это есть удвоенное произведение членов 2x и 3y, то есть 2 × 2x × 3y = 12xy.
Очевидно, что переменная a в данном случае равна 2x, а переменная b равна 3y
a = 2x
b = 3y
Тогда можно сделать вывод, что когда-то выражение 4x2 + 12xy + 9y2 выглядело в виде квадрата суммы (2x + 3y)2, но в результате применения формулы квадрата суммы оно обратилось в многочлен 4x2 + 12xy + 9y2. Наша задача — вернуть ему былую форму, то есть представить в виде (2x + 3y)2
4x2 + 12xy + 9y2 = (2x + 3y)2
А поскольку (2x + 3y)2 это произведение двух сомножителей, каждый из которых равен многочлену (2x + 3y), то исходный многочлен 4x2 + 12xy + 9y2 можно представить в виде разложения на множители (2x + 3y) и (2x + 3y)
4x2 + 12xy + 9y2 = (2x + 3y)(2x + 3y)
Полностью решение можно записать так:
4x2 + 12xy + 9y2 = (2x)2 + 2 × 2x × 3y + (3y)2 = (2x + 3y)2 = (2x + 3y)(2x + 3y)
Пример 2. Разложить на множители многочлен x2 + 12x + 36
Первый член данного многочлена является результатом возведения в квадрат одночлена x, поскольку x2 = x2, третий член — результатом возведения в квадрат числа 6, поскольку 62 = 36, а член 12x это удвоенное произведение членов x и 6, поскольку 2 × x × 6 = 12x.
Воспользуемся формулой a2 + 2ab + b2 = (a + b)2. Роль переменной a играет одночлен x, а роль переменной b играет одночлен 6. Отсюда:
x2 + 12x + 36 = (x + 6)2
А поскольку (x + 6)2 это произведение двух сомножителей, каждый из которых равен многочлену (x + 6), то исходный многочлен x2 + 12x + 36 можно представить в виде разложения на множители (x + 6) и (x + 6)
x2 + 12x + 36 = (x + 6)(x + 6)
Разложение многочлена на множители по формуле квадрата разности двух выражений
Как и по формуле квадрата суммы двух выражений, многочлен можно разложить на множители по формуле квадрата разности двух выражений.
Формула квадрата разности двух выражений выглядит так:
(a − b)2 = a2 − 2ab + b2
Если в этой формуле поменять местами левую и правую часть, то получим:
a2 − 2ab + b2 = (a − b)2
Поскольку правая часть это произведение двух сомножителей, каждый из которых равен (a − b), то многочлен вида a2 − 2ab + b2 можно разложить на множители (a − b) и (a − b).
a2 − 2ab + b2 = (a − b)(a − b)
Пример 1. Разложить на множители многочлен 9x2 − 12xy + 4y2
Чтобы воспользоваться формулой a2 − 2ab + b2 = (a − b)2, нужно узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в квадрат одночлена 3x, поскольку (3x)2 = 9x2. Третий член 4y2 является результатом возведения в квадрат одночлена 2y, поскольку (2y)2 = 4y2, а член 12xy это удвоенное произведение членов 3x и 2y, то есть 2 × 3x × 2y = 12xy.
Очевидно, что переменная a в данном случае равна 3x, а переменная b равна 2y
a = 3x
b = 2y
Тогда можно сделать вывод, что когда-то выражение 9x2 − 12xy + 4y2 выглядело в виде квадрата разности (3x − 2y)2, но в результате применения формулы квадрата разности оно обратилось в многочлен 9x2 − 12xy + 4y2. Наша задача — вернуть ему былую форму, то есть представить в виде (3x − 2y)2
9x2 − 12xy + 4y2 = (3x − 2y)2
А поскольку (3x − 2y)2 это произведение двух сомножителей, каждый из которых равен многочлену (3x − 2y), то исходный многочлен 9x2 − 12xy + 4y2 можно представить в виде разложения на множители (3x − 2y) и (3x − 2y)
9x2 − 12xy + 4y2 = (3x − 2y)(3x − 2y)
Полностью решение можно записать так:
9x2 − 12xy + 4y2 = (3x)2 − 2 × 3x × 2y + (2y)2 = (3x − 2y)2 = (3x − 2y)(3x − 2y)
Пример 2. Разложить на множители многочлен x2 − 4x + 4
Воспользуемся формулой квадрата разности двух выражений:
x2 − 4x + 4 = x2 − 2 × x × 2 + 22 = (x − 2)2 = (x − 2)(x − 2)
Разложение многочлена на множители по формуле куба суммы двух выражений
Вспомним, как выглядит формула куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Поменяем местами левую и правую часть, получим:
a3 + 3a2b + 3ab2 + b3 = (a + b)3
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)3 представляет собой перемножение трёх сомножителей, каждый из которых равен многочлену (a + b).
Стало быть, если нам встретится выражение вида a3 + 3a2b +3ab2 + b3, то мы можем представить его в виде произведения (a + b)(a + b)(a + b). Иными словами, разложить на множители (a + b), (a + b) и (a + b).
a3 + 3a2b + 3ab2 + b3 = (a + b)(a + b)(a + b)
Пример 1. Разложить на множители многочлен m3 + 6m2n + 12mn2 + 8n3
Прежде чем применять формулу куба суммы, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб суммы двух выражений.
Чтобы убедиться, что исходное выражение является кубом суммы двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в куб одночлена m
m3 = m3
Последний член 8n3 является результатом возведения в куб одночлена 2n
(2n)3 = 8n3
Второй член 6m2n является утроенным произведением квадрата первого выражения m и последнего 2n
3 × m2 × 2n = 6m2n
Третий член 12mn2 является утроенным произведением первого выражения m и квадрата последнего выражения 2n
3 × m × (2n)2 = 3 × m × 4n2 = 12mn2
То есть исходный многочлен m3 + 6m2n + 12mn2 + 8n3 по всем параметрам соответствует кубу суммы двух выражений. Переменной a в данном многочлене соответствует m, а переменной b соответствует 2n
a = m
b = 2n
Тогда можно сделать вывод, что когда-то выражение m3 + 6m2n + 12mn2 + 8n3 выглядело в виде куба суммы (m + 2n)3, но в результате применения формулы куба суммы оно обратилось в многочлен m3 + 6m2n + 12mn2 + 8n3. Наша задача — вернуть ему былую форму, то есть представить в виде (m + 2n)3
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)3
А поскольку (m + 2n)3 это произведение трёх сомножителей, каждый из которых равен многочлену (m + 2n), то исходный многочлен m3 + 6m2n + 12mn2 + 8n3 можно представить в виде разложения на множители (m + 2n), (m + 2n) и (m + 2n)
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)(m + 2n)(m + 2n)
Пример 2. Разложить на множители многочлен 125x3 + 75x2 + 15x + 1
Первый член данного многочлена является результатом возведения в куб одночлена 5x
(5x)3 = 125x3
Последний член 1 является результатом возведения в куб одночлена 1
13 = 1
Второй член 75x2 является утроенным произведением квадрата первого выражения 5x и последнего 1
3 × (5x)2 × 1 = 3 × 25x2 = 75x2
Третий член 15x является утроенным произведением первого выражения 5x и квадрата второго выражения 1
3 × 5x × 12 = 15x
Воспользуемся формулой a3 + 3a2b + 3ab2 + b3 = (a + b)3. Роль переменной a играет одночлен 5x, а роль переменной b играет одночлен 1
a = 5x
b = 1
Поэтому,
125x3 + 75x2 + 15x + 1 = (5x + 1)3
А поскольку (5x + 1)3 это произведение трёх сомножителей, каждый из которых равен многочлену (5x + 1), то исходный многочлен 125x3 + 75x2 + 15x + 1 можно представить в виде разложения на множители (5x + 1), (5x + 1) и (5x + 1)
125x3 + 75x2 + 15x + 1 = (5x + 1)(5x + 1)(5x + 1)
Разложение многочлена на множители по формуле куба разности двух выражений
Как и по формуле куба суммы двух выражений, многочлен можно разложить на множители по формуле куба разности двух выражений.
Вспомним, как выглядит формула куба разности двух выражений:
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Если в этой формуле поменять местами левую и правую часть, то получим:
a3 − 3a2b + 3ab2 − b3 = (a − b)3
Поскольку правая часть это произведение трёх сомножителей, каждый из которых равен (a − b), то многочлен вида a3 − 3a2b + 3ab2 − b3 можно разложить на множители (a − b), (a − b) и (a − b).
a3 − 3a2b + 3ab2 − b3 = (a − b)(a − b)(a − b)
Пример 1. Разложить на множители многочлен 64 − 96x + 48x2 − 8x3
Прежде чем применять формулу куба разности, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб разности двух выражений.
Чтобы убедиться, что исходное выражение является кубом разности двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в куб одночлена 4
43 = 64
Последний член 8x3 является результатом возведения в куб одночлена 2x
(2x)3 = 8x3
Второй член 96x является утроенным произведением квадрата первого выражения 4 и последнего 2x
3 × 42 × 2x = 3 × 16 × 2x = 96x
Третий член 48x2 является утроенным произведением первого выражения 4 и квадрата второго выражения 2x
3 × 4 × (2x)2 = 3 × 4 × 4x2 = 48x2
Видим, что исходный многочлен 64 − 96x + 48x2 − 8x3 по всем параметрам соответствует кубу разности двух выражений. Переменной a в данном многочлене соответствует 4, а переменной b соответствует 2x
a = 4
b = 2x
Тогда можно сделать вывод, что когда-то выражение 64 − 96x + 48x2 − 8x3 выглядело в виде куба разности (4 − 2x)3, но в результате применения формулы куба разности оно обратилось в многочлен 64 − 96x + 48x2 − 8x3. Наша задача — вернуть ему былую форму, то есть представить в виде (4 − 2x)3
64 − 96x + 48x2 − 8x3 = (4 − 2x)3
А поскольку (4 − 2x)3 это произведение трёх сомножителей, каждый из которых равен (4 − 2x), то исходный многочлен 64 − 96x + 48x2 − 8x3 можно представить в виде разложения на множители (4 − 2x), (4 − 2x) и (4 − 2x)
64 − 96x + 48x2 − 8x3 = (4 − 2x)(4 − 2x)(4 − 2x)
Пример 2. Разложить на множители многочлен 27 − 135x + 225x2 − 125x3
Первый член данного многочлена является результатом возведения в куб одночлена 3
33 = 27
Последний член 125 является результатом возведения в куб одночлена 5x
(5x)3 = 125x3
Второй член 135x является утроенным произведением квадрата первого выражения 3 и последнего 5x
3 × 32 × 5x = 3 × 9 × 5x = 135x
Третий член 225x2 является утроенным произведением первого выражения 3 и квадрата второго выражения 5x
3 × 3 × (5x)2 = 3 × 3 × 25x2 = 225x2
Воспользуемся формулой a3 − 3a2b + 3ab2 − b3 = (a − b)3. Роль переменной a играет одночлен 3, а роль переменной b играет одночлен 5x
a = 3
b = 5x
Поэтому,
27 − 135x + 225x2 − 125x3 = (3 − 5x)3
А поскольку (3 − 5x)3 это произведение трёх сомножителей, каждый из которых равен многочлену (3 − 5x), то исходный многочлен 27 − 135x + 225x2 − 125x3 можно представить в виде разложения на множители (3 − 5x), (3 − 5x) и (3 − 5x)
125x3 + 75x2 + 15x + 1 = (3 − 5x)(3 − 5x)(3 − 5x)
Разложение многочлена на множители по формуле разности квадратов двух выражений
Вспомним, как выглядит формула умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
Если в этой формуле поменять местами левую и правую часть, то получим:
a2 − b2 = (a − b)(a + b)
Эту формулу называют разностью квадратов. Она позволяет разложить выражение вида a2 − b2 на множители (a − b) и (a + b).
Пример 1. Разложить на множители многочлен 16x2 − 25y2
Чтобы воспользоваться формулой a2 − b2 = (a − b)(a + b), следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член 16x2 является результатом возведения в квадрат одночлена 4x
(4x)2 = 16x2
Второй член 25y2 является результатом возведения в квадрат одночлена 5y
(5y)2 = 25y2
То есть в данном случае переменной a соответствует одночлен 4x, а переменной b соответствует одночлен 5y
a = 4x
b = 5y
Теперь можно воспользоваться формулой a2 − b2 = (a − b)(a + b). Подставим в неё наши значения a и b
(4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
Полностью решение можно записать так:
16x2 − 25y2 = (4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
Для проверки можно выполнить умножение (4x − 5y)(4x + 5y). Если мы всё сделали правильно, то должны получить 16x2 − 25y2
(4x − 5y)(4x + 5y) = 16x2 − 20xy + 20xy − 25y2 = 16x2 − 25y2
Пример 2. Разложить на множители многочлен x2 − y2
В данном случае переменной a соответствует x, а переменной b соответствует y. Тогда по формуле квадрата разности имеем:
x2 − y2 = (x − y)(x + y)
Случай как в данном примере является наиболее простым, поскольку здесь сразу видно чему равно a и чему равно b.
Чаще всего члены, из которых состоит исходная разность, являются результатами возведения во вторую степень каких-нибудь одночленов. Чтобы узнать чему в таком случае равны a и b, нужно как в первом примере представить члены исходной разности в виде одночленов возведённых в квадрат.
Например, чтобы разложить многочлен 4x4 − 9y6 на множители, нужно исходные члены представить в виде одночленов возведённых в квадрат. Первый член в виде одночлена, возведенного в квадрат, можно записать как (2x2)2, поскольку вычисление этого выражение даёт в результате 4x4
(2x2)2 = 4x4
А член 9y6 в виде одночлена, возведенного в квадрат, можно записать как (3y3)2, поскольку вычисление этого выражение даёт в результате 9y6
(3y3)2 = 9y6
Теперь мы знаем, чему равны a и b. Они равны 2x2 и 3y3 соответственно. Подставим их в формулу a2 − b2 = (a − b)(a + b)
(2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Полностью решение можно записать так:
4x4 − 9y6 = (2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Несмотря на простоту разложения по формуле разности квадратов, частые ошибки приходятся именно на эти задачи. Чтобы убедиться, что задача решена правильно, не мешает выполнить умножение в получившемся разложении. Если задача решена правильно, то должен получиться изначальный многочлен.
Проверим умножением данный пример. У нас должен получиться многочлен 4x4 − 9y6
(2x2 − 3y3)(2x2 + 3y3) = 2x2(2x2 + 3y3) − 3y3(2x2 + 3y3)
= 4x4 + 6x2y3 − 6x2y3 − 9y6 = 4x4 − 9y6
Пример 4. Разложить на множители многочлен 81 − 64
Представим члены исходной разности в виде одночленов возведенных в квадрат. Далее воспользуемся формулой разности квадратов:
81 − 64 = 92 − 82 = (9 − 8)(9 + 8)
Разложение многочлена на множители по формуле сумме кубов двух выражений
Мы помним, что произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений:
(a + b)(a2 − ab + b2) = a3 + b3
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую суммой кубов двух выражений:
a3 + b3 = (a + b)(a2 − ab + b2)
Эта формула позволяет разложить выражение вида a3 + b3 на множители (a + b) и (a2 − ab + b2).
Пример 1. Разложить на множители многочлен 27x3 + 64y3
Представим члены 27x3 и 64y3 в виде одночленов, возведённых в куб
27x3 + 64y3 = (3x)3 + (4y)3
Теперь воспользуемся формулой суммы кубов. Переменная a в данном случае равна 3x, переменная b равна 4y
27x3 + 64y3 = (3x)3 + (4y)3 = (3x + 4y)((3x)2 − 3x × 4y + (4y)2) =
(3x + 4y)(9x2 − 12xy + 16y2)
Пример 2. Разложить на множители многочлен 125 + 8
Представим члены 125 и 8 в виде одночленов, возведённых в куб:
125 + 8 = 53 + 23
Далее воспользуемся формулой суммы кубов:
125 + 8 = 53 + 23 = (5 + 2)(25 − 10 + 4)
Разложение многочлена на множители по формуле разности кубов двух выражений
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений:
(a − b)(a2 + ab + b2) = a3 − b3
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую разностью кубов двух выражений:
a3 − b3 = (a − b)(a2 + ab + b2)
Эта формула позволяет разложить выражение вида a3 − b3 на множители (a − b) и (a2 + ab + b2).
Пример 1. Разложить на множители многочлен 64x3 − 27y3
Представим члены 64x3 и 27y3 в виде одночленов, возведённых в куб:
64x3 − 27y3 = (4x)3 − (3y)3
Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 4x, переменная b равна 3y
64x3 − 27y3 = (4x)3 − (3y)3 = (4x − 3y)((4x)2 + 4x × 3y + (3y)2) =
(4x − 3y)(16x2 + 12xy + 9y2)
Пример 2. Разложить на множители многочлен 64 − 27
Представим члены 64 и 27 в виде одночленов, возведённых в куб:
64 − 27 = 43 − 33 = (4 − 3)(16 + 12 + 9)
Пример 3. Разложить на множители многочлен 125x3 − 1
Представим члены 125x3 и 1 в виде одночленов, возведённых в куб:
125x3 − 1 = (5x)3 − 13
Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 5x, переменная b равна 1
125x3 − 1 = (5x)3 − 13 = (5x − 1)((5x)2 + 5x × 1 + 12) =
(5x − 1)(25x2 + 5x + 1)
Разложение многочлена на множители различными способами
К некоторым многочленам можно применять различные способы разложения на множители. Например, к одному многочлену можно применить способ вынесения общего за скобки, а затем воспользоваться одной из формул сокращённого умножения.
Пример 1. Разложить на множители многочлен ax2 − ay2
В данном многочлене содержится общий множитель a. Вынесем его за скобки:
ax2 − ay2 = a(x2 − y2)
При этом в скобках образовался многочлен, который является разностью квадратов. Применив формулу разности квадратов. Тогда получим:
ax2 − ay2 = a(x2 − y2) = a(x − y)(x + y)
Пример 2. Разложить на множители многочлен 3x2 + 6xy + 3y2
Вынесем за скобки общий множитель 3
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2)
В скобках образовался многочлен, который является квадратом суммы двух выражений, а именно выражений x и y. Тогда этот квадрат суммы можно представить как (x + y)2 и далее записать в виде двух сомножителей, каждый из которых равен (x + y)
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2) = 3(x + y)2 = 3(x + y)(x + y)
Задания для самостоятельного решения
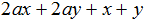

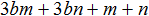
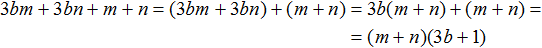
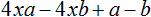
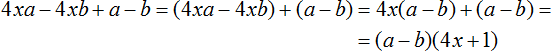
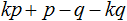
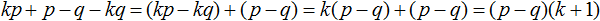
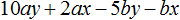

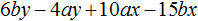
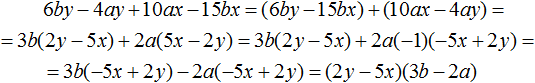

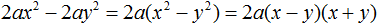
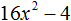
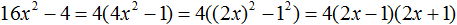

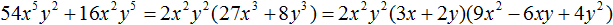

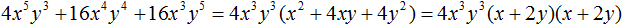
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Формулы сокращённого умножения
Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.
Квадрат суммы двух выражений
Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.
Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)
(2x + 3y)2 = (2x + 3y)(2x + 3y)
Получили умножение многочлена на многочлен. Выполним его:
(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4x2 + 6xy + 6xy + 9y2 = 4x2 + 12xy + 9y2
То есть выражение (2x + 3y)2 равно 4x2 + 12xy + 9y2
(2x + 3y)2 = 4x2 + 12xy + 9y2
Решим аналогичный пример, который попроще:
(a + b)2
Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)
(a + b)2 = (a + b)(a + b)
Выполним это умножение:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
То есть выражение (a + b)2 равно a2 + 2ab + b2
(a + b)2 = a2 + 2ab + b2
Оказывается, что случай (a + b)2 можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y
a = 2x
b = 3y
И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:
(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4x2 + 12xy + 9y2
Как и в прошлый раз получили многочлен 4x2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:
(2x + 3y)2 = 4x2 + 12xy + 9y2
Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.
Первый способ:
(2 + 3)2 = 52 = 25
Второй способ:
(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25
Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9
Значит, (5a + 3)2 = 25a2 + 30a + 9.
Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:
(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9
Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.
Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2
Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b
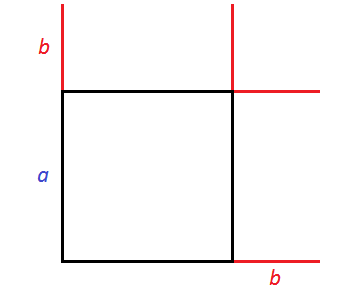
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:
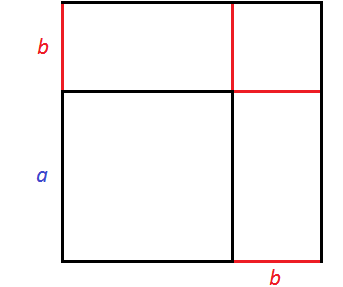
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.
Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b
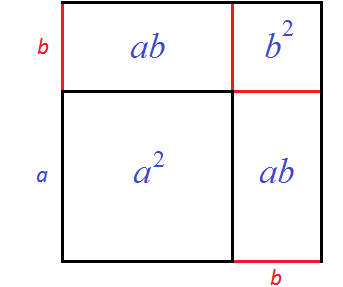
В результате получается следующая сумма площадей:
a2 + ab + ab + b2
Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Квадрат разности двух выражений
Формула квадрата разности двух выражений выглядит следующим образом:
(a − b)2 = a2 − 2ab + b2
Эту формулу можно прочитать так:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)
(a − b)2 = (a − b)(a − b)
Если выполнить это умножение, то получится многочлен a2 − 2ab + b2
(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2
Пример 1. Преобразовать выражение (7x − 5)2 в многочлен.
Воспользуемся формулой квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49x2 − 70x + 25
Значит, (7x − 5)2 = 49x2 − 70x + 25.
Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:
(7x − 5)2 = (7x − 5)(7x − 5) = 49x2 − 35x − 35x + 25 = 49x2 − 70x + 25.
Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2
Рассмотрим следующий рисунок:
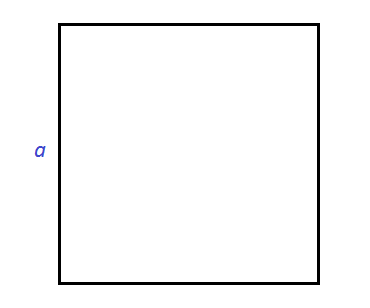
Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b
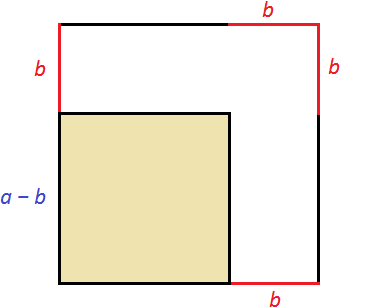
Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:
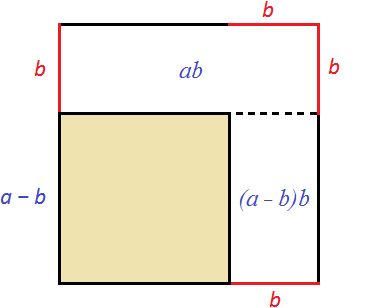
Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b
a2 − ab − (a − b)b
Раскроем скобки в выражении (a − b)b
a2 − ab − ab + b2
Приведем подобные слагаемые:
a2 − 2ab + b2
В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.
Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.
Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.
(5x − 2y)2
a = 5x
b = 2y
(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25x2 − 20xy + 4y2
Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:
(5x − 2y)2 = (5x + (−2y))2
и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:
(5x + (−2y)2
a = 5x
b = −2y
(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25x2 − 20xy + 4y2
Исключением могут быть выражения вида (x − (−y))2. В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)
(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2
Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:
(x + y)2 = x2 + 2xy + y2
Куб суммы и куб разности
Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Формулу куба суммы двух выражений можно прочитать так:
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
А формулу куба разности двух выражений можно прочитать так:
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.
Выведем формулу куба суммы самостоятельно:
(a + b)3
Выражение (a + b)3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)
(a + b)3 = (a + b)(a + b)(a + b)
Но выражение (a + b)3 также может быть записано как (a + b)(a + b)2
(a + b)3 = (a + b)(a + b)2
При этом сомножитель (a + b)2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a2 + 2ab + b2.
Тогда (a + b)3 можно записать как (a + b)(a2 + 2ab + b2).
(a + b)3 = (a + b)(a2 + 2ab + b2)
А это есть умножение многочлена на многочлен. Выполним его:
(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
Аналогично можно вывести формулу куба разности двух выражений:
(a − b)3 = (a − b)(a2 − 2ab + b2) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3
Пример 1. Преобразуйте выражение (x + 1)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3x2 + 3x + 1
Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:
(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2x2 + x + x2 + 2x + 1 = x3 + 3x2 + 3x + 1
Пример 2. Преобразовать выражение (6a2 + 3b3)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(6a2 + 3b3)3 = (6a2)3 + 3 × (6a2)2 × 3b3 + 3 × 6a2 × (3b3)2 + (3b3)3 = 216a6 + 3 × 36a4 × 3b3 + 3 × 6a2 × 9b6 + 27b9
Пример 3. Преобразовать выражение (n2 − 3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4 + 27n2 − 27
Пример 4. Преобразовать выражение (2x2 − x3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(2x2 − x3)3 = (2x2)3 − 3 × (2x2)2 × x3 + 3 × 2x2 × (x3)2 − (x3)3 =
8x6 − 3 × 4x4 × x3 + 3 × 2x2 × x6 − x9 =
8x6 − 12x7 + 6x8 − x9
Умножение разности двух выражений на их сумму
Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:
(a − b)(a + b)
В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:
(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2
То есть выражение (a − b)(a + b) равно a2 − b2
(a − b)(a + b) = a2 − b2
Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.
Пример 1. Выполнить умножение (2x − 5)(2x + 5)
В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:
(2x − 5)(2x + 5) = (2x)2 − 52
Вычислим правую часть, получим 4x2 − 25
(2x − 5)(2x + 5) = (2x)2 − 52 = 4x2 − 25
Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4x2 − 25
(2x − 5)(2x + 5) = 4x2 − 10x + 10x − 25 = 4x2 − 25
Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16x2 − 25y2
Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2
В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.
Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.
Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.
Пример 3. Выполнить умножение (7 + 3x)(3x − 7)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(7 + 3x)(3x − 7) = (3x)2 − 72 = 9x2 − 49
Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)
(a − b)(a + b) = a2 − b2
(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6
Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)
В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)
Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)
Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.
Далее вычисляем выражение в скобках:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25x2 − 9y2)
Теперь умножим −1 на выражение в скобках и получим окончательный результат:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) =
−1(25x2 − 9y2) = −25x2 + 9y2
Умножение разности двух выражений на неполный квадрат их суммы
Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:
(a − b)(a2 + ab + b2)
Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a2 + ab + b2) является неполным квадратом суммы этих двух выражений.
Неполный квадрат суммы это многочлен вида a2 + ab + b2. Он похож на обычный квадрат суммы a2 + 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4x2 + 6xy + 9y2 является неполным квадратом суммы выражений 2x и 3y.
Действительно, первый член выражения 4x2 + 6xy + 9y2, а именно 4x2 является квадратом выражения 2x, поскольку (2x)2 = 4x2. Третий член выражения 4x2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.
Итак, умножим разность (a − b) на неполный квадрат суммы a2 + ab + b2
(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) =
a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3
То есть выражение (a − b)(a2 + ab + b2) равно a3 − b3
(a − b)(a2 + ab + b2) = a3 − b3
Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.
Пример 1. Выполнить умножение (2x − 3y)(4x2 + 6xy + 9y2)
Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. Второй многочлен 4x2 + 6xy + 9y2 это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3. В нашем случае умножение (2x − 3y)(4x2 + 6xy + 9y2) можно заменить на разность кубов 2x и 3y
(2x − 3y)(4x2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8x3 − 27y3
Попробуем решить этот же пример, не пользуясь формулой (a − b)(a2 + ab + b2) = a3 − b3. У нас получится тот же результат, но решение станет длиннее:
(2x − 3y)(4x2 + 6xy + 9y2) = 2x(4x2 + 6xy + 9y2) − 3y(4x2 + 6xy + 9y2) =
8x3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8x3 − 27y3
Пример 2. Выполнить умножение (3 − x)(9 + 3x + x2)
Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3
(3 − x)(9 + 3x + x2) = 33 − x3 = 27 − x3
Умножение суммы двух выражений на неполный квадрат их разности
Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:
(a + b)(a2 − ab + b2)
Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a2 − ab + b2) является неполным квадратом разности этих двух выражений.
Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4x2 − 6xy + 9y2 является неполным квадратом разности выражений 2x и 3y.
(2x)2 − 2x × 3y + (3y)2 = 4x2 − 6xy + 9y2
Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a2 − ab + b2
(a + b)(a2 − ab + b2) = a(a2 − ab + b2) + b(a2 − ab + b2) =
a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3
То есть выражение (a + b)(a2 − ab + b2) равно a3 + b3
(a + b)(a2 − ab + b2) = a3 + b3
Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:
Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.
Пример 1. Выполнить умножение (2x + 3y)(4x2 − 6xy + 9y2)
Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y, а второй многочлен 4x2 − 6xy + 9y2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3. В нашем случае умножение (2x + 3y)(4x2 − 6xy + 9y2) можно заменить на сумму кубов 2x и 3y
(2x + 3y)(4x2 − 6xy + 9y2) = (2x)3 + (3y)3 = 8x3 + 27y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
(2x + 3y)(4x2 − 6xy + 9y2) = 2x(4x2 − 6xy + 9y2) + 3y(4x2 − 6xy + 9y2) =
8x3 − 12x2y + 18xy2 + 12x2y − 18xy2 + 27y3 = 8x3 + 27y3
Пример 2. Выполнить умножение (2x + y)(4x2 − 2xy + y2)
Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x2 − 2xy + y2) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3
(2x + y)(4x2 − 2xy + y2) = (2x)3 + y3 = 8x3 + y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
(2x + y)(4x2 − 2xy + y2) = 2x(4x2 − 2xy + y2) + y(4x2 − 2xy + y2) =
8x3 − 4x2y + 2xy2 + 4x2y − 2xy2 + y3 = 8x3 + y3
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Многочлены
Определения и примеры
Многочлен — это сумма одночленов.
Например, выражение 2x + 4xy2 + x + 2xy2 является многочленом. Проще говоря, многочлен это несколько одночленов, соединенных знаком «плюс».
В некоторых многочленах одночлены могут соединяться знаком «минус». Например, 3x − 5y − 2x. Следует иметь ввиду, что это по-прежнему сумма одночленов. Многочлен 3x − 5y − 2x это сумма одночленов 3x, −5y и − 2x, то есть 3x + (−5y) + (−2x). После раскрытия скобок образуется многочлен 3x − 5y − 2x.
3x + (−5y) + (−2x) = 3x − 5y − 2x
Соответственно, рассматривая по отдельности каждый одночлен многочлена, его нужно рассматривать вместе со знаком, который перед ним располагается. Так, в многочлене 3x − 5y − 2x минус перед одночленом 5y относится к коэффициенту 5, а минус перед одночленом 2x относится к коэффициенту 2. Чтобы не противоречить определению многочлена, вычитание можно заменять сложением:
3x − 5y − 2x = 3x + (−5y) + (−2x)
Но это действие нагромождает многочлен скобками, поэтому вычитание на сложение не заменяют, учитывая в будущем, что каждый одночлен многочлена будет рассматриваться вместе со знаком, который перед ним располагается.
Одночлены, из которых состоит многочлен, называют членами многочлена.
Если многочлен состоит из двух членов, то такой многочлен называют двучленом. Например, многочлен x + y является двучленом.
Если многочлен состоит из трёх членов, то такой многочлен называют трехчленом. Например, многочлен x + y + z является трехчленом.
Если какой-нибудь многочлен содержит обычное число, то это число называют свободным членом многочлена. Например, в многочлене 3x + 5y + z + 7 член 7 является свободным членом. Свободный член многочлена не содержит буквенной части.
Многочленом также является любое числовое выражение. Так, следующие выражения являются многочленами:
2 + 3
5 + 3 + 2
5 − 4 + 9
Сложение многочленов
К многочлену можно прибавить другой многочлен. Например, прибавим к многочлену 2x + y многочлен 3x + y.
Заключим в скобки каждый многочлен и соединим их знаком «плюс», указывая тем самым, что мы складываем многочлены:
(2x + y) + (3x + y)
Теперь раскрываем скобки:
2x + y + 3x + y
Далее приведём подобные слагаемые:
2x + y + 3x + y = 5x + 2y
Таким образом, при сложении многочленов 2x + y и 3x + y получается многочлен 5x + 2y.
Разрешается также сложение многочленов в столбик. Для этого их следует записать так, чтобы подобные слагаемые располагались друг под другом, затем выполнить самó сложение. Решим предыдущий пример в столбик:
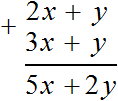
Если в одном из многочленов окажется слагаемое, которое не имеет подобного слагаемого в другом многочлене, оно переносится к результату без изменений. Как говорят при сложении обычных чисел — «сносится».
Например, сложим в столбик многочлены 2x2 + y3 + z + 2 и 5x2 + 2y3. Для начала запишем их так, чтобы подобные слагаемые располагались друг под другом, затем выполним их сложение. Обнаруживаем, что во втором многочлене не содержатся слагаемые, которые можно было бы сложить со слагаемыми z и 2 из первого многочлена. Поэтому слагаемые z и 2 переносятся к результату без изменений (вместе со своими знаками)
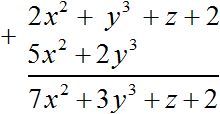
Решим этот же пример с помощью скобок:
(2x2 + y3 + z + 2) + (5x2 + 2y3) = 2x2 + y3 + z + 2 + 5x2 + 2y3 = (2x2 + 5x2) + (y3 + 2y3) + z + 2 = 7x2 + 3y3 + z + 2
Пример 3. Сложить многочлены 7x3 + y + z2 и x3 − z2
Решим этот пример в столбик. Запишем второй многочлен под первым так, чтобы подобные слагаемые располагались друг под другом:
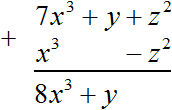
Во втором многочлене не было слагаемого, которого можно было бы сложить со слагаемым y из первого многочлена, поэтому это слагаемое было перенесёно к результату без изменений. А сложение подобных слагаемых z2 и −z2 дало в результате 0. Ноль по традиции не записываем. Поэтому окончательный ответ это 8x3 + y.
Решим этот же пример с помощью скобок:
(7x3 + y + z2) + (x3 − z2) = 7x3 + y + z2 + x3 − z2 = (7x3 + x3) + (z2 − z2) + y = 8x3 + y
Вычитание многочленов
Из многочлена можно вычесть другой многочлен. Например, вычтем из многочлена 2x + y многочлен 3x + y.
Заключим в скобки каждый многочлен и соединим их знаком «минус», указывая тем самым, что мы выполняем вычитание:
(2x + y) − (3x + y)
Теперь раскроем скобки:
2x + y − 3x − y
Приведём подобные слагаемые. Слагаемые y и −y являются противоположными. Сумма противоположных слагаемых равна нулю
y + (−y) = 0
Приводя подобные слагаемые, мы обычно складываем их. Но в качестве знака операции можно использовать знак одночлена. Так, приводя подобные слагаемые y и −y мы сложили их по правилу приведения подобных слагаемых. Но можно не складывая, записать их друг за другом
y − y
Получится тот же результат, поскольку выражения y + (−y) и y − y одинаково равны нулю:
y − y = 0
Возвращаемся к нашему примеру. Вычеркнем члены y и −y:
![]()
А сложение подобных слагаемых 2x и −3x, даст в результате −x
2x + (−3x) = −x
Или без сложения, записав члены друг за другом:
2x − 3x = −x
Значит, при вычитании из многочлена (2x + y) многочлена (3x + y) получится одночлен −x.
Решим этот же пример в столбик:
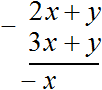
Пример 2. Вычесть из многочлена 13x − 11y + 10z многочлен −15x + 10y − 15z
Решим этот пример с помощью скобок, а затем в столбик:
(13x − 11y + 10z) − (−15x + 10y − 15z) = 13x − 11y + 10z + 15x − 10y + 15z = (13x + 15x) + (−11y − 10y) + (10z + 15z) = 28x + (−21y) + 25z = 28x − 21y + 25z
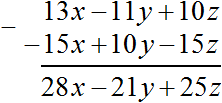
Следует быть внимательным при вычитании в столбик. Если не следить за знаками, вероятность допустить ошибку очень высокá. Нужно учитывать не только знак операции вычитания, но и знак располагающийся перед слагаемым.
Так, в данном примере из слагаемого 10z вычиталось слагаемое −15z
10z − (−15z)
Результат вычисления этого выражения должен быть положительным, поскольку 10z − (−15z) = 10z + 15z.
Складывая или вычитая многочлены при помощи скобок, первый многочлен в скобки можно не заключать. Так, в данном примере из многочлена 13x − 11y + 10z требовалось вычесть многочлен −15x + 10y − 15z
Вычитание было записано так:
(13x − 11y + 10z) − (−15x + 10y − 15z)
Но первый многочлен можно не заключать в скобки:
13x − 11y + 10z − (−15x + 10y − 15z)
Заключение первого многочлена в скобки на первых порах позволяет начинающим наглядно увидеть, что второй многочлен полностью вычитается из первого, а не из определенной его части.
Представление многочлена в виде суммы или разности
Многочлен можно представить в виде суммы или разности многочленов. По сути это обратное действие раскрытию скобок, поскольку идея подразумевает, что имеется некий многочлен, и из него можно образовать сумму или разность многочленов, заключив в скобки некоторые из членов исходного многочлена.
Пусть имеется многочлен 3x + 5y + z + 7. Представим его в виде суммы двух многочленов.
Итак, из членов исходного многочлена нужно образовать два многочлена, сложенные между собой. Давайте заключим в скобки члены 3x и 5y, а также члены z и 7. Далее объединим их с помощью знака «плюс»
(3x + 5y) + (z + 7)
Значение исходного многочлена при этом не меняется. Если раскрыть скобки в получившемся выражении (3x + 5y) + (z + 7), то снова получим многочлен 3x + 5y + z + 7.
(3x + 5y) + (z + 7) = 3x + 5y + z + 7
В скобки также можно было бы заключить члены 3x, 5y, z и прибавить это выражение в скобках к члену 7
(3x + 5y + z) + 7
Представляя многочлен в виде разности многочленов, нужно придерживаться следующего правила. Если члены заключаются в скобки после знака минуса, то этим членам внутри скобок нужно поменять знаки на противоположные.
Вернемся к многочлену 3x + 5y + z + 7. Представим его в виде разности двух многочленов. Давайте заключим в скобки многочлен 3x и 5y, а также z и 7, затем объединим их знаком «минус»
(3x + 5y) − (z + 7)
Но мы видим, что после знака минуса следует заключение членов z и 7 в скобки. Поэтому этим членам нужно поменять знаки на противоположные. Делать это нужно внутри скобок:
(3x + 5y) − (−z − 7)
Заключая члены в скобки, нужно следить за тем, чтобы значение нового выражения тождественно было равно предыдущему выражению. Этим и объясняется замена знаков членов внутри скобок. Если в выражении (3x + 5y) − (−z − 7) раскрыть скобки, то получим изначальный многочлен 3x + 5y + z + 7.
(3x + 5y) − (−z − 7) = 3x + 5y + z + 7
Вообще, представляя многочлен в виде суммы или разности, можно придерживаться следующих правил:
Если перед скобками ставится знак «плюс», то все члены внутри скобок записываются со своими же знаками.
Если перед скобками ставится знак «минус», то все члены внутри скобок записываются с противоположными знаками.
Пример 1. Представить многочлен 3x4 + 2x3 + 5x2 − 4 в виде суммы каких-нибудь двучленов:
(3x4 + 2x3) + (5x2 − 4)
Пример 2. Представить многочлен 3x4 + 2x3 + 5x2 − 4 в виде разности каких-нибудь двучленов:
(3x4 + 2x3) − (−5x2 + 4)
Перед вторыми скобками располагался минус, поэтому члены 5x2 и −4 были записаны с противоположными знаками.
Многочлен и его стандартный вид
Многочлен, как и одночлен, можно привести к стандартному виду. В результате получается упрощенный многочлен, с которым удобно работать.
Чтобы привести многочлен к стандартному виду, нужно привести подобные слагаемые в этом многочлене. Подобные слагаемые в многочлене называют подобными членами многочлена, а приведение подобных слагаемых в многочлене — приведением его подобных членов.
Подобные члены многочлена это члены, имеющие одинаковую буквенную часть.
Приведём многочлен 2x + 4xy2 + x − xy2 к стандартному виду. Для этого приведём его подобные члены. Подобными членами в этом многочлене являются 2x и x, а также 4xy2 и −xy2.
![]()
В результате получили многочлен 3x + 3xy2, который не имеет подобных членов. Такой вид многочлена называют многочленом стандартного вида.
Как и у одночлена, у многочлена имеется степень. Чтобы определить степень многочлена, сначала его нужно привести к стандартному виду, затем выбрать тот одночлен, степень которого является наибольшей из всех.
В предыдущем примере мы привели многочлен 2x + 4xy2 + x − xy2 к стандартному виду. В результате получили многочлен 3x + 3xy2. Он состоит из двух одночленов. Степенью первого одночлена является 1, а степенью второго одночлена является 3. Наибольшая из этих степеней является 3. Значит, многочлен 3x + 3xy2 является многочленом третьей степени.
А поскольку многочлен 3x + 3xy2 тождественно равен предыдущему многочлену 2x + 4xy2 + x − xy2, то и этот предыдущий многочлен является многочленом третьей степени.
Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в него одночленов.
В некоторых многочленах прежде всего требуется привести к стандартному виду одночлены, входящие в него, и только потом приводить сам многочлен к стандартному виду.
Например, приведем многочлен 3xx4 + 3xx3 − 5x2x3 − 5x2x к стандартному виду. Этот многочлен состоит из одночленов, которые не приведены к стандартному виду. Сначала приведём их к стандартному виду:
3xx4 + 3xx3 − 5x2x3 − 5x2x = 3x5 + 3x4 − 5x5 − 5x3
Теперь получившийся многочлен 3x5 + 3x4 − 5x5 − 5x3 можно привести к стандартному виду. Для этого приведем его подобные члены. Подобными являются члены 3x5 и −5x5. Больше подобных членов нет. Члены 3x4 и −5x3 будут переписаны без изменений:
3xx4 + 3xx3 − 5x2x3 − 5x2x = 3x5 + 3x4 − 5x5 − 5x3 = −2x5 + 3x4 − 5x3
Пример 2. Привести многочлен 3ab + 4cc + ab + 3c2 к стандартному виду.
Сначала приведем одночлен 4cc, входящий в исходный многочлен, к стандартному виду, получим 4с2
3ab + 4cc + ab + 3c2 = 3ab + 4с2 + ab + 3c2
Далее приведём подобные члены:
3ab + 4cc + ab + 3c2 = 3ab + 4с2 + ab + 3c2 = 4ab + 7c2
Пример 3. Привести многочлен 4x2 − 4y − x2 + 17y − y к стандартному виду.
Подобными членами в данном многочлене являются 4x2 и −x2, а также −4y, 17y и −y. Приведем их:
4x2 − 4y − x2 + 17y − y = 3x2 + 12y
Приводя подобные члены, можно использовать скобки. Для этого подобные члены следует заключить в скобки, затем объединить выражения в скобках с помощью знака «плюс».
Решим предыдущий пример с помощью скобок. Подобными членами в нём были 4x2 и −x2, а также −4y, 17y и −y. Заключим их в скобки и объединим с помощью знака «плюс»
4x2 − 4y − x2 + 17y − y = (4x2 − x2) + (−4y + 17y − y)
Теперь в скобках выполним приведение подобных членов:
4x2 − 4y − x2 + 17y − y = (4x2 − x2) + (−4y + 17y − y) = (3x2) + (12y)
В получившемся выражении (3x2) + (12y) раскроем скобки:
4x2 − 4y − x2 + 17y − y = (4x2 − x2) + (−4y + 17y − y) = (3x2) + (12y) = 3x2 + 12y
Конечно, такой подход нагромождает выражение, но зато позволяет свести к минимуму допущение ошибок.
Пример 4. Привести многочлен 12x2 − 9y − 9x2 + 6y + y к стандартному виду.
Заключим в скобки подобные слагаемые и объединим их с помощью знака «плюс»
12x2 − 9y − 9x2 + 6y + y = (12x2 − 9x2) + (−9y + 6y + y)
Далее вычисляем содержимое скобок:
12x2 − 9y − 9x2 + 6y + y = (12x2 − 9x2) + (−9y + 6y + y) = (3x2) + (−2y)
Избавляемся от скобок при помощи раскрытия:
12x2 − 9y − 9x2 + 6y + y = (12x2 − 9x2) + (−9y + 6y + y) = (3x2) + (−2y) = 3x2 − 2y
Изменение порядка следования членов
Рассмотрим двучлен x − y. Как сделать так, чтобы член −y располагался первым, а член x вторым?
Многочлен это сумма одночленов. То есть исходный двучлен двучлен x − y является суммой x и −y
x + (−y)
От перестановки мест слагаемых сумма не меняется. Тогда x и −y можно поменять местами
−y + x
Пример 2. В двучлене −y − x поменять местами члены.
Двучлен −y − x это сумма членов −y и −x
−y + (−x)
Тогда согласно переместительному закону сложения получим (−x) + (−y). Избавим выражение от скобок:
−x − y
Таким образом, решение можно записать покороче:
−y − x = −x − y
Пример 3. Упорядочить члены многочлена x + xy3 − x2 в порядке убывания степеней.
Наибольшую степень в данном многочлене имеет член xy3, далее −x2, а затем x. Запишем их в этом порядке:
x + xy3 − x2 = xy3 − x2 + x
Умножение одночлена на многочлен
Одночлен можно умножить на многочлен. Чтобы умножить одночлен на многочлен, нужно этот одночлен умножить на каждый член многочлена и полученные произведения сложить.
Например, умножим одночлен 3x2 на многочлен 2x + y + 5. При умножении одночлена на многочлен, последний нужно заключать в скобки:
3x2(2x + y + 5)
Теперь умножим одночлен 3x2 на каждый член многочлена 2x + y + 5. Получающиеся произведения будем складывать:
3x2(2x + y + 5) = 3x2 × 2x + 3x2 × y + 3x2 × 5
Вычислим получившиеся произведения:
3x2(2x + y + 5) = 3x2 × 2x + 3x2 × y + 3x2 × 5 = 6x3 + 3x2y + 15x2
Таким образом, при умножении одночлена 3x2 на многочлен 2x + y + 5 получается многочлен 6x3 + 3x2y + 15x2.
Умножение желательно выполнять в уме. Так решение получается короче:
3x2(2x + y + 5) = 6x3 + 3x2y + 15x2
В некоторых примерах одночлен располагается после многочлена. В этом случае опять же каждый член многочлена нужно перемножить с одночленом и полученные произведения сложить.
Например, предыдущий пример мог быть дан в следующем виде:
(2x + y + 5) × 3x2
В этом случае мы умножили бы каждый член многочлен (2x + y + 5) на одночлен 3x2 и сложили бы полученные результаты:
(2x + y + 5) × 3x2 = 2x × 3x2 + y × 3x2 + 5 × 3x2 = 6x3 + 3x2y + 15x2
Умножение одночлена на многочлен (или умножение многочлена на одночлен) основано на распределительном законе умножения.
a(b + c) = ab + ac
То есть чтобы умножить число a на сумму b + c, нужно число a умножить на каждое слагаемое суммы b + c, и полученные произведения сложить.
Вообще, умножение одночлена на многочлен, да и распределительный закон умножения имеют геометрический смысл.
Допустим, имеется прямоугольник со сторонами a и b

Увеличим сторону b на c

Достроим отсутствующую сторону и закрасим для наглядности получившийся прямоугольник:

Теперь вычислим площадь получившегося большого прямоугольника. Он включает в себя желтый и серый прямоугольники.
Чтобы вычислить площадь получившегося большого прямоугольника, можно по отдельности вычислить площади желтого и серого прямоугольников и сложить полученные результаты. Площадь желтого прямоугольника будет равна ab, а площадь серого ac
ab + ac
А это всё равно что длину большого прямоугольника умножить на его ширину. Длина в данном случае это b + c, а ширина это a
(b + c) × a
или ширину умножить на длину, чтобы расположить буквы a, b и c в алфавитном порядке:
a × (b + c)
Таким образом, выражения a × (b + c) и ab + ac равны одному и тому же значению (одной и той же площади)
a × (b + c) = ab + ac
К примеру, пусть у нас имеется прямоугольник длиной 4 см, и шириной 2 см, и мы увеличили длину на 2 см
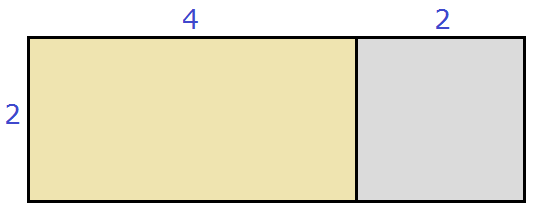
Тогда площадь данного прямоугольника будет равна 2 × (4 + 2) или сумме площадей желтого и серого прямоугольников: 2 × 4 + 2 × 2. Выражения 2 × (4 + 2) и 2 × 4 + 2 × 2 равны одному и тому же значению 12
2 × (4 + 2) = 12
2 × 4 + 2 × 2 = 12
Поэтому,
2 × (4 + 2) = 2 × 4 + 2 × 2 = 12.
Действительно, в получившемся большом прямоугольнике содержится двенадцать квадратных сантиметров:
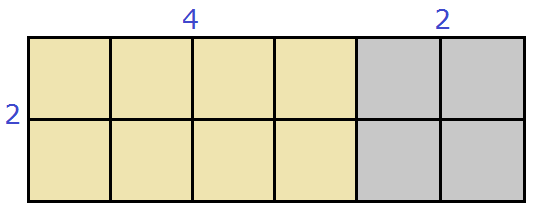
Пример 2. Умножить одночлен 2a на многочлен a2 − 7a − 3
Умножим одночлен 2a на каждый член многочлена a2 − 7a − 3 и сложим полученные произведения:
2a(a2 − 7a − 3) = 2a × a2 + 2a × (−7a) + 2a × (−3) = 2a3 + (−14a2) + (−6a) = 2a3 − 14a2 − 6a
Или покороче:
2a(a2 − 7a − 3) = 2a3 − 14a2 − 6a
Пример 3. Умножить одночлен −a2b2 на многочлен a2b2 − a2 − b2
Умножим одночлен −a2b2 на каждый член многочлена a2b2 − a2 − b2 и сложим полученные произведения:
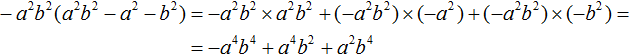
Или покороче:
![]()
Пример 4. Выполнить умножение −1,4x2y6(5x3y − 1,5xy2 − 2y3)
Умножим одночлен −1,4x2y6 на каждый член многочлена 5x3y − 1,5xy2 − 2y3 и сложим полученные произведения:
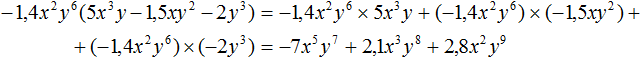
Или покороче:
![]()
Пример 5. Выполнить умножение 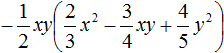
Умножим одночлен ![]() на каждый член многочлена
на каждый член многочлена ![]() и сложим полученные произведения:
и сложим полученные произведения:

Или покороче:
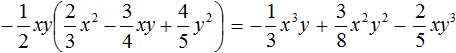
Выполняя короткие решения, результаты записывают сразу друг за другом вместе со знаком полученного члена. Рассмотрим поэтапно, как было выполнено короткое решение данного примера.
Сначала одночлен ![]() нужно умножить на первый член многочлена
нужно умножить на первый член многочлена 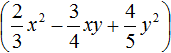 , то есть на
, то есть на ![]() . Умножение выполняется в уме. Получается результат
. Умножение выполняется в уме. Получается результат ![]() . В исходном выражении ставим знак равенства и записываем первый результат:
. В исходном выражении ставим знак равенства и записываем первый результат:
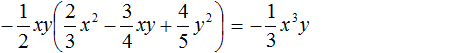
После этого в исходном выражении никаких знаков ставить нельзя. Нужно сразу приступать к следующему умножению.
Следующим шагом будет умножение одночлена ![]() на второй член многочлена
на второй член многочлена 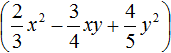 , то есть на
, то есть на ![]() . Получается результат
. Получается результат ![]() . Этот результат является положительным, то есть со знаком плюс
. Этот результат является положительным, то есть со знаком плюс ![]() . В исходном выражении этот результат записывается вместе с этим плюсом сразу после члена
. В исходном выражении этот результат записывается вместе с этим плюсом сразу после члена ![]()
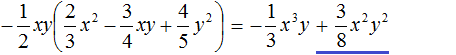
После этого в исходном выражении никаких знаков ставить нельзя. Нужно сразу приступать к следующему умножению.
Следующим шагом будет умножение одночлена ![]() на третий член многочлена
на третий член многочлена 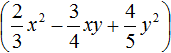 , то есть на
, то есть на ![]() . Получается результат
. Получается результат ![]() . Этот результат является отрицательным, то есть со знаком минус. В исходном выражении этот результат записывается вместе со своим минусом сразу после члена
. Этот результат является отрицательным, то есть со знаком минус. В исходном выражении этот результат записывается вместе со своим минусом сразу после члена ![]()
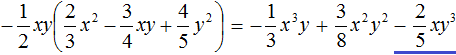
Иногда встречаются выражения, в которых сначала нужно выполнить умножение одночлена на многочлен, затем опять на одночлен. Например:
2(a + b)c
В этом примере сначала член 2 умножается на многочлен (a + b), затем результат умножается на c. Для начала выполним умножение 2 на (a + b) и заключим полученный результат в скобки
2(a + b)c = (2a + 2b)с
Скобки говорят о том, что результат умножения 2 на (a + b) полностью умножается на c. Если бы мы не заключили скобки 2a + 2b, то получилось бы выражение 2a + 2b × с, в котором на с умножается только 2b. Это привело бы к изменению значения изначального выражения, а это недопустимо.
Итак, получили (2a + 2b)с. Теперь умножаем многочлен (2a + 2b) на одночлен c и получаем окончательный результат:
2(a + b)c = (2a + 2b)с = 2ac + 2bc
Умножение также можно было бы выполнить сначала умножив (a + b) на с и полученный результат перемножить с членом 2
2(a + b)c = 2(ac + bc) = 2ac + 2bc
В данном случае срабатывает сочетательный закон умножения, который говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий:
a × b × с = (a × b) × с = a × (b × с)
То есть умножение можно выполнять в любом порядке. Это не приведёт к изменению значения изначального выражения.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, нужно каждый член первого многочлена умножить на каждый член второго многочлена и полученные произведения сложить.
Например, умножим многочлен x + 3 на y + 4
Заключим в скобки каждый многочлен и объединим их знаком умножения ×
(x + 3) × (y + 4)
Либо запишем их друг за другом без знака ×. Это тоже будет означать умножение:
(x + 3)(y + 4)
Теперь умножим каждый член первого многочлена (x + 3) на каждый член второго многочлена (y + 4). Здесь опять же будет применяться распределительный закон умножения:
(a + b)c= ac + bc
Отличие в том, что у нас вместо переменной c имеется многочлен (y + 4), состоящий из членов y и 4. Наша задача умножить (x + 3) сначала на y, затем на 4. Чтобы не допустить ошибку, можно представить, что члена 4 пока не существует вовсе. Для этого его можно закрыть рукой:
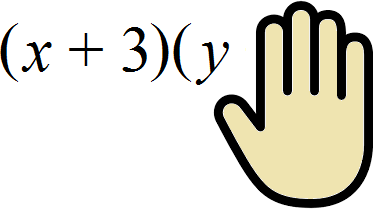
Получаем привычное для нас умножение многочлена на одночлен. А именно, умножение многочлена (x + 3) на одночлен y. Выполним это умножение:
(x + 3)(y + 4) = xy + 3y
Мы умножили (x + 3) на y. Теперь осталось умножить (x + 3) на 4. Для этого умножаем каждый член многочлена (x + 3) на одночлен 4. На этот раз в исходном выражении (x + 3)(y + 4) рукой закроем y, поскольку на него мы уже умножали многочлен (x + 3)

Получаем умножение многочлена (x + 3) на одночлен 4. Выполним это умножение. Умножение необходимо продолжать в исходном примере (x + 3)(y + 4) = xy + 3y
(x + 3)(y + 4) = xy + 3y + 4x + 12
Таким образом, при умножении многочлена (x + 3) на многочлен (y + 4) получается многочлен xy + 3y + 4x + 12.
По другому умножение многочлена на многочлен можно выполнить ещё так: каждый член первого многочлена умножить на второй многочлен целиком и полученные произведения сложить.
Решим предыдущий пример, воспользовавшись этим способом. Умножим каждый член многочлена x + 3 на весь многочлен y + 4 целиком и сложим полученные произведения:
(x + 3)(y + 4) = x(y + 4) + 3(y + 4)
В результате приходим к умножению одночлена на многочлен, которое мы изучили ранее. Выполним это умножение:
(x + 3)(y + 4) = x(y + 4) + 3(y + 4) = xy + 4x + 3y + 12
Получится тот же результат что и раньше, но члены полученного многочлена будут располагаться немного по другому.
Умножение многочлена на многочлен имеет геометрический смысл. Допустим, имеется прямоугольник, длина которого a и ширина b
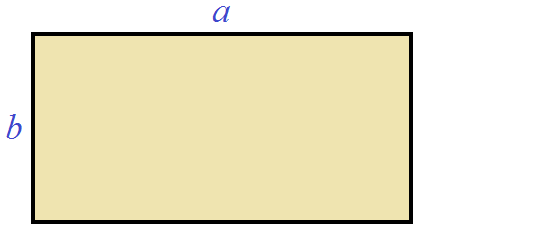
Площадь этого прямоугольника будет равна a × b.
Увеличим длину данного прямоугольника на x, а ширину на y
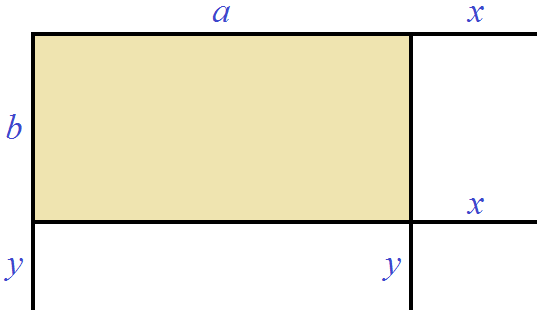
Достроим отсутствующие стороны и закрасим для наглядности получившиеся прямоугольники:
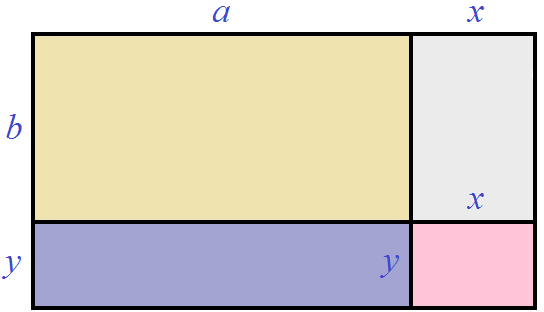
Теперь вычислим площадь получившегося большого прямоугольника. Для этого вычислим по отдельности площадь каждого прямоугольника, входящего в этот большой прямоугольник и сложим полученные результаты. Площадь жёлтого прямоугольника будет равна ab, площадь серого xb, площадь фиолетового ay, площадь розового xy
ab + xb + ay + xy
А это всё равно что умножить длину получившегося большого прямоугольника на его ширину. Длина в данном случае это a + x, а ширина b + y
(a + x)(b + y)
То есть выражения (a + x)(b + y) и ab + xb + ay + xy тождественно равны
(a + x)(b + y) = ab + xb + ay + xy
Представим, что у нас имелся прямоугольник, длиной 6 см и шириной 3 см, и мы увеличили его длину на 2 см, а ширину на 1 см
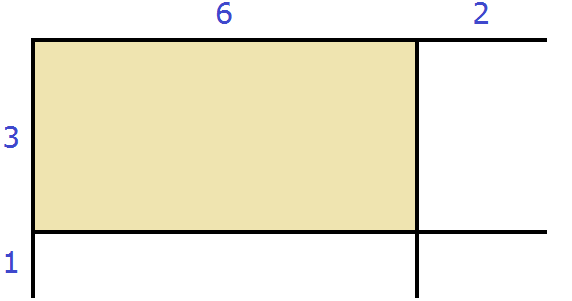
Достроим отсутствующие стороны и закрасим для наглядности получившиеся прямоугольники:
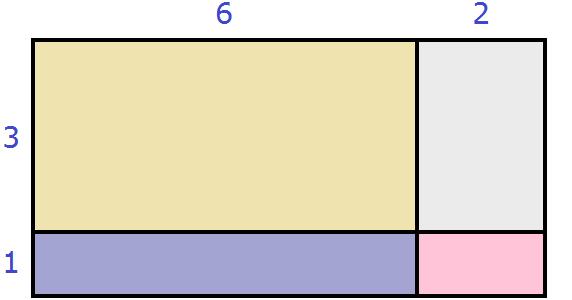
Площадь получившегося большого прямоугольника будет равна (6 + 2)(3 + 1) или сумме площадей прямоугольников, входящих в большой прямоугольник: 6 × 3 + 2 × 3 + 6 × 1 + 2 × 1. В обоих случаях получим один и тот же результат 32
(6 + 2)(3 + 1) = 32
6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 = 32
Поэтому,
(6 + 2)(3 + 1) = 6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 = 18 + 6 + 6 + 2 = 32
Действительно, в получившемся большом прямоугольнике содержится тридцать два квадратных сантиметра:
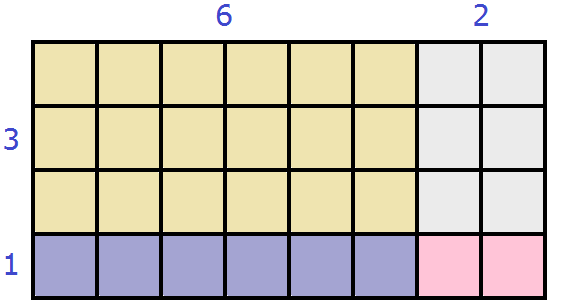
Пример 2. Умножить многочлен a + b на c + d
Заключим исходные многочлены в скобки и запишем их друг за другом:
(a + b)(c + d)
Теперь умножим каждый член первого многочлена (a + b) на каждый член второго многочлена (c + d)
(a + b)(c + d) = ac + bc + ad + bd
Пример 4. Выполнить умножение (−x − 2y)(x + 2y2)
Умножим каждый член многочлена (−x − 2y) на каждый член многочлена (x + 2y2)
(−x − 2y)(x + 2y2) = −x2 − 2xy − 2xy2 − 4y3
Результат перемножения членов нужно записывать вместе со знаками этих членов. Рассмотрим поэтапно, как был решён данный пример.
Итак, требуется умножить многочлен (−x − 2y) на многочлен (x + 2y2). Сначала надо умножить многочлен (−x − 2y) на первый член многочлена (x + 2y2), то есть на x.
Умножаем −x на x, получаем −x2. В исходном выражении (−x − 2y)(x + 2y2) ставим знак равенства и записываем −x2
(−x − 2y)(x + 2y2) = −x2
После этого в исходном выражении никаких знаков ставить нельзя. Нужно сразу приступать к следующему умножению. А именно умножению −2y на x . Получится −2xy. Этот результат является отрицательным, то есть со знаком минус. В исходном выражении записываем результат −2xy сразу после члена −x2
(−x − 2y)(x + 2y2) = −x2 − 2xy
Теперь умножаем многочлен (−x − 2y) на второй член многочлена (x + 2y2), то есть на 2y2
Умножаем −x на 2y2, получаем −2xy2. В исходном выражении записываем этот результат сразу после члена −2xy
(−x − 2y)(x + 2y2) = −x2 − 2xy − 2xy2
Приступаем к следующему умножению. А именно умножению −2y на 2y2. Получаем −4y3. В исходном выражении этот результат записываем вместе со своим минусом сразу после члена −2xy2
(−x − 2y)(x + 2y2) = −x2 − 2xy − 2xy2 − 4y3
Пример 5. Выполнить умножение (4a2 + 2ab − b2)(2a − b)
Умножим каждый член многочлена (4a2 + 2ab − b2) на каждый член многочлена (2a − b)
![]()
В получившемся выражении можно привести подобные слагаемые:
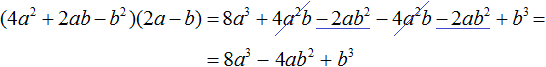
Пример 6. Выполнить умножение −(a + b)(с − d)
В этот раз перед скобками располагается минус. Этот минус является коэффициентом −1. То есть исходное выражение является произведением трёх сомножителей: −1, многочлена (a + b) и многочлена (с − d).
−1(a + b)(с − d)
Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то его можно вычислять в любом порядке.
Поэтому сначала можно перемножить многочлены (a + b) и (с − d) и полученный в результате многочлен умножить на −1. Перемножение многочленов (a + b) и (с − d) нужно выполнять в скобках
−1(a + b)(с − d) = −1(ac + bc − ad − bd)
Теперь перемножаем −1 и многочлен (ac + bc − ad − bd). В результате все члены многочлена (ac + bc − ad − bd) поменяют свои знаки на противоположные:
−1(a + b)(с − d) = −1(ac + bc − ad − bd) = −ac − bc + ad + bd
Либо можно было перемножить −1 с первым многочленом (a + b) и результат перемножить с многочленом (с − d)
−1(a + b)(с − d) = (−a − b)(с − d) = −ac − bc + ad + bd
Пример 7. Выполнить умножение x2(x + 5)(x − 3)
Сначала перемножим многочлены (x + 5) и (x − 3), затем полученный в результате многочлен перемножим с x2
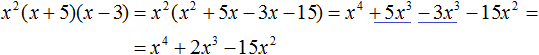
Пример 8. Выполнить умножение (a + 1)(a + 2)(a + 3)
Сначала перемножим многочлены (a + 1) и (a + 2), затем полученный многочлен перемножим с многочленом (a + 3)
Итак, перемножим (a + 1) и (a + 2)
![]()
Полученный многочлен (a2 + a + 2a + 2) перемножим с (a + 3)
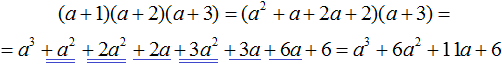
Если быстрое перемножение многочленов на первых порах даётся тяжело, можно воспользоваться подробным решением, суть которого заключается в том, чтобы записать, как каждый член первого многочлена умножается на весь второй многочлен целиком. Такая запись хоть и занимает место, но позволяет свести к минимуму допущение ошибок.
Например, выполним умножение (a + b)(c + d)
Запишем как каждый член многочлена a + b умножается на весь многочлен c + d целиком. В результате придём к умножению одночлена на многочлен, выполнять которое проще:
(a + b)(c + d) = a(с + d) + b(с + d) = aс + ad + bс + bd
Такая запись удобна при умножении двучлена на какой-нибудь многочлен, в котором содержится больше двух членов. Например:
(x + y)(x2 + 2xy + y2) = x(x2 + 2xy + y2) + y(x2 + 2xy + y2) = x3 + 2x2y + xy2 + x2y + 2xy2 + y3 = x3 + 3x2y + 3xy2 + y3
Или при перемножении многочленов, содержащих больше двух членов. Например, умножим многочлен x2 + 2x − 5 на многочлен x3 − x + 2
(x2 + 2x − 5)(x3 − x + 2)
Запишем перемножение исходных многочленов в виде умножения каждого члена многочлена x2 + 2x − 5 на многочлен x3 − x + 2.
![]()
Получили привычное для нас умножения одночленов на многочлены. Выполним эти умножения:
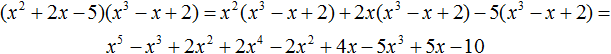
В получившемся многочлене приведём подобные члены:
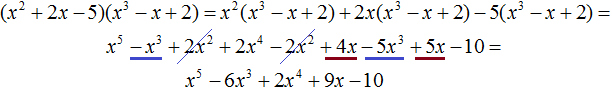
Одночлены, входящие в получившийся многочлен, расположим в порядке убывания степеней. Делать это необязательно. Но такая запись будет красивее:

Вынесение общего множителя за скобки
Мы уже учились выносить общий множитель за скобки в простых буквенных выражениях. Теперь мы немного углубимся в эту тему, и научимся выносить общий множитель за скобки в многочлене. Принцип вынесения будет таким же, как и в простом буквенном выражении. Небольшие трудности могут возникнуть лишь с многочленами, состоящими из степеней.
Рассмотрим простой двучлен 6xy + 3xz. Вынесем в нём общий множитель за скобки. В данном случае за скобки можно вынести общий множитель 3x. Напомним, что при вынесении общего множителя за скобки, каждое слагаемое исходного выражения надо разделить на этот общий множитель:
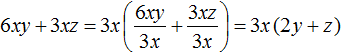
Или покороче:
![]()
В результате получили 3x(2y + z). При этом в скобках образовался другой более простой многочлен (2y + z). Выносимый за скобки общий множитель выбирают так, чтобы в скобках остались члены, которые не содержат общего буквенного множителя, а модули коэффициентов этих членов не имели общего делителя, кроме единицы.
Поэтому в приведенном примере за скобки был вынесен общий множитель 3x. В скобках образовался многочлен 2y + z, модули коэффициентов которого не имеют общего делителя кроме единицы. Это требование можно выполнить, если найти наибольший общий делитель (НОД) модулей коэффициентов исходных членов. Этот НОД станóвится коэффициентом общего множителя, выносимого за скобки. В нашем случае исходный многочлен был 6xy + 3xz. Коэффициенты исходных членов это числа 6 и 3, а их НОД равен 3.
А буквенную часть общего множителя выбирают так, чтобы члены в скобках не имели общих буквенных множителей. В данном случае это требование выполнилось легко. Общий буквенный множитель был виден невооруженным глазом — это был множитель x.
Пример 2. Вынести общий множитель за скобки в многочлене x2 + x + xy
Все члены данного многочлены имеют коэффициент единицу. Наибольший общий делитель модулей из этих единиц есть единица. Поэтому числовая часть выносимого за скобки множителя будет единицей. Но единицу в качестве коэффициента не записывают.
Далее выбираем буквенную часть общего множителя. Прежде всего надо понимать, что любой член, входящий в многочлен, является одночленом. А одночлен это произведение чисел, переменных и степеней. Даже если членом многочлена является обычное число, его всегда можно представить в виде произведения единицы и самого этого числа. Например, если в многочлене содержится число 5, его можно представить в виде 1 × 5. Если в многочлене содержится число 8, то его можно представить в виде произведения множителей 2 × 2 × 2 (или как 2 × 4)
С переменными такая же ситуация. Если в многочлене содержится член, являющийся переменной или степенью, их всегда можно представить в виде произведения. К примеру, если многочлен содержит одночлен x, его можно представить в виде произведения 1 × x. Если же многочлен содержит одночлен x3, его можно представить в виде произведения xxx.
Одночлены, из которых состоит многочлен x2 + x + xy, можно разложить на множители так, чтобы мы смогли увидеть буквенный сомножитель, который является общим для всех членов.
Итак, первый член многочлена x2 + x + xy, а именно x2 можно представить в виде произведения x × x. Второй член x можно представить в виде 1 × x. А третий член xy оставим без изменения, или для наглядности перепишем его с помощью знака умножения x × y
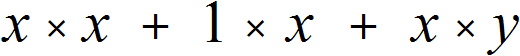
Каждый член многочлена представлен в виде произведения множителей, из которых состоят эти члены. Легко заметить, что во всех трёх произведениях общим сомножителем является x. Выделим его:
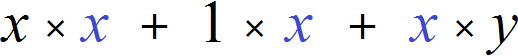
Этот множитель x и вынесем за скобки. Опять же при вынесении общего множителя за скобки каждое слагаемое исходного выражения делим на этот общий множитель. В нашем случае каждый член многочлена x × x + 1 × x + x × y нужно разделить на общий множитель x
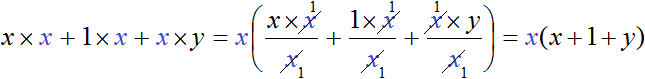
Значит, при вынесении общего множителя за скобки в многочлене x2 + x + xy, получается x(x + 1 + y)
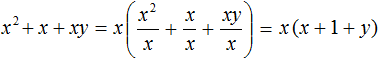
Или покороче:
![]()
В результате в скобках остаются члены, которые не имеют общих буквенных сомножителей, а модули коэффициентов этих членов не имеют общих делителей, кроме 1.
Пример 2. Вынести общий множитель за скобки в многочлене 15x2y3 + 12xy2 + 3xy2
Определим коэффициент общего множителя, выносимого за скобки. Наибольший общий делитель модулей коэффициентов 15, 12 и 3 это число 3. Значит, число 3 будет коэффициентом общего множителя, выносимого за скобки.
Теперь определим буквенную часть общего множителя, выносимого за скобки. Её нужно выбирать так, чтобы в скобках остались члены, которые не содержат общего буквенного множителя.
Перепишем буквенные части исходного многочлена 15x2y3 + 12xy2 + 3xy2 в виде разложения на множители. Это позволит хорошо увидеть, что именно можно вынести за скобки:
![]()
Видим, что среди буквенных частей общим множителем является xyy, то есть xy2. Если вынести этот множитель за скобки, в скобках останется многочлен, не имеющий общего буквенного множителя.
В итоге общим множителем, выносимым за скобки, будет множитель 3xy2
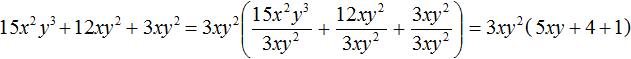
Или покороче:
![]()
Для проверки можно выполнить умножение 3xy2(5xy + 4 + 1). В результате должен получиться многочлен 15x2y3 + 12xy2 + 3xy2
3xy2(5xy + 4 + 1) = 3xy2 × 5xy + 3xy2 × 4 + 3xy2 × 1 = 15x2y3 + 12xy2 + 3xy2
Пример 3. Вынести общий множитель за скобки в выражении x2 + x
В данном случае за скобки можно вынести x
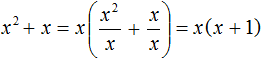
Это потому что первый член x2 можно представить как xx. А второй член x представить как 1 × x
x2 + x = xx + 1 × x
Не следует на письме подробно расписывать содержимое каждого члена, разлагая его на множители. Это легко делается в уме.
Пример 4. Вынести общий множитель за скобки в многочлене 5y2 − 15y
В данном случае за скобки можно вынести 5y. Наибольший общий делитель модулей коэффициентов 5 и 15 это число 5. Среди буквенных множителей общим является y
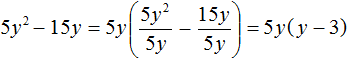
Пример 5. Вынести общий множитель за скобки в многочлене 5y2 − 15y3
В данном примере за скобки можно вынести 5y2. Наибольший общий делитель модулей коэффициентов 5 и 15 это число 5. Среди буквенных множителей общим является y2
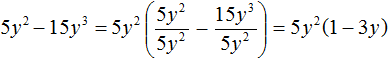
Пример 6. Вынести общий множитель за скобки в многочлене 20x4 − 25x2y2 − 10x3
В данном примере за скобки можно вынести 5x2. Наибольший общий делитель модулей коэффициентов 20, −25 и −10 это число 5. Среди буквенных множителей общим является x2
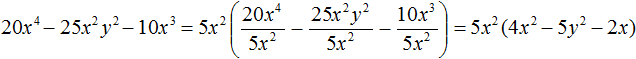
Пример 7. Вынести общий множитель за скобки в многочлене am + am + 1
Второй член am + 1 представляет собой произведение из am и a, поскольку am × a = am + 1
Заменим в исходном примере член am + 1 на тождественно равное ему произведение am × a. Так проще будет увидеть общий множитель:
![]()
Теперь можно увидеть, что общим множителем является am. Его и вынесем за скобки:
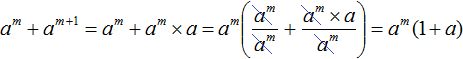
Проверка на тождественность
Решение задачи с многочленами порой растягивается на несколько строк. Каждое следующее преобразование должно быть тождественно равно предыдущему. Если возникают сомнения в правильности своих действий, то можно подставить произвольные значения переменных в исходное и полученное выражение. Если исходное и полученное выражение будут равны одному и тому же значению, то можно быть уверенным, что задача была решена правильно.
Допустим, нам нужно вынести общий множитель за скобки в следующем многочлене:
2x + 4x2
В данном случае за скобки можно вынести общий множитель 2x
2x + 4x2 = 2x(1 + 2x)
Представим, что мы не уверены в таком решении. В этом случае нужно взять любое значение переменной x и подставить его сначала в исходное выражение 2x + 4x2, затем в полученное 2x(1 + 2x). Если в обоих случаях результат будет одинаковым, то это будет означать, что задача решена правильно.
Возьмём произвольное значение x и подставим его в исходное выражение 2x + 4x2. Пусть x = 2. Тогда получим:
2x + 4x2 = 2 × 2 + 4 × 22 = 4 + 16 = 20
Теперь подставим значение 2 в преобразованное выражение 2x(1 + 2x)
2x(1 + 2x) = 2 × 2 × (1 + 2 × 2) = 4 × 5 = 20
То есть при x = 2 выражения 2x + 4x2 и 2x(1 + 2x) равны одному и тому же значению. Это значит, что задача была решена правильно. Тоже самое будет происходить и при других значениях переменных x. Например, проверим наше решение при x = 1
2x + 4x2 = 2 × 1 + 4 × 12 = 2 + 4 = 6
2x(1 + 2x) = 2 × 1 × (1 + 2 × 1) = 2 × 3 = 6
Пример 2. Вычесть из многочлена 5x2 − 3x + 4 многочлен 4x2 − x и проверить полученный результат, подставив вместо переменной x произвольное значение.
Выполним вычитание:
![]()
Мы выполнили два преобразования: cначала раскрыли скобки, а затем привели подобные члены. Теперь проверим эти два преобразования на тождественность. Пусть x = 2. Подставим это значение сначала в исходное выражение, а затем в преобразованные:
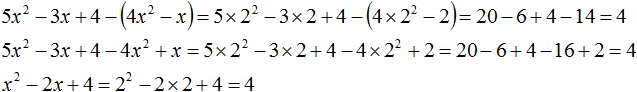
Видим, что при каждом преобразовании значение выражения при x = 2 не менялось. Это значит, что задача была решена правильно.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Одночлены
Определения и примеры
Одночлен — это произведение чисел, переменных и степеней. Например, выражения 5a, 3ab2 и −62aa2b3 являются одночленами.
Приведём ещё примеры одночленов:
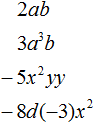
Одночленом также является любое отдельное число, любая переменная или любая степень. Например, число 9 является одночленом, переменная x является одночленом, степень 52 является одночленом.
Приведение одночлена к стандартному виду
Рассмотрим следующий одночлен:
![]()
Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.
Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.
Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.
Итак, приведём одночлен 3a25a3b2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:
15
Далее в одночлене 3a25a3b2 содержатся степени a2 и a3, которые имеют одинаковое основание a. Из тождественных преобразований со степенями известно, что при перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают. Тогда перемножение степеней a2 и a3 даст в результате a5. Записываем a5 рядом с числом 15
15a5
Далее в одночлене 3a25a3b2 содержится степень b2. Её не с чем перемножать, поэтому она остаётся без изменений. Записываем её как есть к новому одночлену:
15a5b2
Мы привели одночлен 3a25a3b2 к стандартному виду. В результате получили одночлен 15a5b2
3a25a3b2 = 15a5b2
Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.
Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc
abc = 1 × abc
А коэффициентом одночлена −abc будет −1, поскольку −abc это произведение минус единицы и abc
−abc = −1 × abc
Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.
Например, степенью одночлена 15a5b2 является 7. Это потому что переменная a имеет показатель 5, а переменная b имеет показатель 2. Отсюда 5 + 2 = 7. Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.
Ещё пример. Степенью одночлена 7ab2 является 3. Здесь переменная a имеет показатель 1, а переменная b имеет показатель 2. Отсюда 1 + 2 = 3.
Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.
Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.
Пример 1. Привести одночлен 5xx3ya2 к стандартному виду
Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:
15
Далее в одночлене 5xx3ya2 содержатся переменные x и x. Перемножим их, получим x2.
15x2
Далее в одночлене 5xx3ya2 содержится переменная y, которую не с чем перемножать. Записываем её без изменений:
15x2y
Далее в одночлене 5xx3ya2 содержится степень a2, которую тоже не с чем перемножать. Её также оставляем без изменений:
15x2ya2
Получили одночлен 15x2ya2, который приведён к стандартному виду. Буквенные сомножители принято записывать в алфавитном порядке. Тогда одночлен 15x2ya2 примет вид 15a2x2y.
Поэтому, 5xx3ya2 = 15a2x2y.
Пример 2. Привести одночлен 2m3n × 0,4mn к стандартному виду
Перемножим числа, переменные и степени по отдельности.
2m3n × 0,4mn = 2 × 0,4 × m3 × m × n × n = 0,8m4n2
Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m3 × m и n × n
2m3n × 0,4mn = (2 × 0,4) × (m3 × m) × (n × n) = 0,8m4n2
Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:
2m3n × 0,4mn = 0,8m4n2
Но чтобы в уме приводить одночлен к стандартному виду, тема умножения целых чисел и умножения степеней должна быть изучена на хорошем уровне.
Сложение и вычитание одночленов
Одночлены можно складывать и вычитать. Чтобы это было возможно, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути приведение подобных слагаемых, которое мы рассматривали при изучении буквенных выражений.
Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.
Пример 1. Сложить одночлены 6a2b и 2a2b
6a2b + 2a2b
Сложим коэффициенты 6 и 2, а буквенную часть 6a2b оставим без изменений
6a2b + 2a2b = 8a2b
Пример 2. Вычесть из одночлена 5a2b3 одночлен 2a2b3
5a2b3 − 2a2b3
Можно заменить вычитание сложением, и сложить коэффициенты одночленов, оставив буквенную часть без изменения:
5a2b3 − 2a2b3 = 5a2b3 + (−2a2b3) = 3a2b3
Либо сразу из коэффициента первого одночлена вычесть коэффициент второго одночлена, а буквенную часть оставить без изменения:
5a2b3 − 2a2b3 = 3a2b3
Умножение одночленов
Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.
Пример 1. Перемножить одночлены 5x и 8y
Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:
5x × 8y = (5 × 8) × (x × y) = 40xy
Пример 2. Перемножить одночлены 5x2y3 и 7x3y2c
Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:
5x2y3 × 7x3y2c = (5 × 7) × (x2x3) × (y3y2) × c = 35x5y5c
Пример 3. Перемножить одночлены −5a2bc и 2a2b4
−5a2bc × 2a2b4 = (−5 × 2) × (a2a2) × (bb4) × c = −10a4b5c
Пример 4. Перемножить одночлены x2y5 и (−6xy2)
x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7
Пример 5. Найти значение выражения ![]()
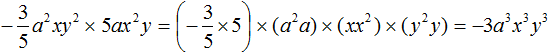
Деление одночленов
Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.
Например, разделим одночлен 8a2b2 на одночлен 4ab. Запишем это деление в виде дроби:
![]()
Первый одночлен 8a2b2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.
Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2. В исходном выражении ставим знак равенства и записываем этот коэффициент частного:
![]()
Теперь делим буквенную часть. В делимом содержится a2, в делителе — просто a. Делим a2 на a, получаем a, поскольку a2 : a = a2 − 1 = a. Записываем в частном a после 2
![]()
Далее в делимом содержится b2, в делителе — просто b. Делим b2 на b, получаем b, поскольку b2 : b = b2 − 1 = b. Записываем в частном b после a
![]()
Значит, при делении одночлена 8a2b2 на одночлен 4ab получается одночлен 2ab.
Сразу можно выполнить проверку. При умножении частного на делитель должно получаться делимое. В нашем случае, если 2ab умножить на 4ab, должно получиться 8a2b2
2ab × 4ab = (2 × 4) × (aa) × (bb) = 8a2b2
Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.
К примеру, одночлен 6xy2 нельзя разделить на одночлен 3xyz. В делителе 3xyz содержится переменная z, которая не содержится в делимом 6xy2.
Проще говоря, мы не сможем найти частное, которое при умножении на делитель 3xyz дало бы делимое 6xy2, поскольку такое умножение обязательно будет содержать переменную z, которой нет в 6xy2.
Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.
Например, при делении одночлена 4x2y2z на 2xy, получается 2xyz. Сначала разделили 4 на 2 получили 2, затем x2 разделили на x, получили x, затем y2 разделили на y, получили y. Затем приступили к делению переменной z на такую же переменную в делителе, но обнаружили, что такой переменной в делителе нет. Поэтому перенесли переменную z в частное без изменений:
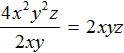
Для проверки умножим частное 2xyz на делитель 2xy. В результате должен получиться одночлен 4x2y2z
2xyz × 2xy = (2 × 2) × (xx) × (yy) × z = 4x2y2z
Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.
Так, в предыдущем примере нельзя было разделить одночлен 6xy2 на одночлен 3xyz. Но можно сократить эту дробь на одночлен 3xy. Напомним, что сокращение дроби это деление числителя и знаменателя на одно и то же число (в нашем случае на одночлен 3xy). В результате сокращения дробь становится проще, но её значение не меняется:
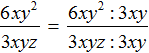
В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:
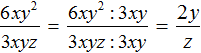
Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:
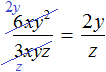
Пример 2. Разделить одночлен 12a2b3c3 на одночлен 4a2bc
![]()
Пример 3. Разделить одночлен x2y3z на одночлен xy2
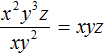
Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.
Например, разделить одночлен 2x на одночлен x2 нельзя, поскольку степень x, входящая в делимое, имеет показатель 1, тогда как степень x2, входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x2 даст в результате делимое 2x.
Конечно, мы можем выполнить деление x на x2, воспользовавшись свойством степени с целым показателем:
![]()
и такое частное при перемножении с делителем x2 будет давать в результате делимое 2x
![]()
Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное ![]() целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.
целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.
Возведение одночлена в степень
Одночлен можно возвести в степень. Для этого используют правило возведения степени в степень.
Пример 1. Возвести одночлен xy во вторую степень.
Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый сомножитель этого одночлена
(xy)2 = x2y2
Пример 2. Возвести одночлен −5a3b во вторую степень.
(−5a3b)2 = (−5)2 × (a3)2 × b2 = 25a6b2
Пример 3. Возвести одночлен −a2bc3 в пятую степень.
В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:
(−a2bc3)5 = (−1)5 × (a2)5 × b5 × (c3)5 = −1a10b5c15 = −a10b5c15
Когда коэффициент равен −1, то саму единицу не записывают. Записывают только минус и потом остальные сомножители одночлена. В приведенном примере сначала получился одночлен −1a10b5c15, затем он был заменён на тождественно равный ему одночлен −a10b5c15.
Пример 4. Представить одночлен 4x2 в виде одночлена, возведённого в квадрат.
В данном примере нужно найти произведение, которое во второй степени будет равно выражению 4x2. Очевидно, что это произведение 2x. Если это произведение возвести во вторую степень (в квадрат), то получится 4x2
(2x)2 = 22x2 = 4x2
Значит, 4x2 = (2x)2. Выражение (2x)2 это и есть одночлен, возведённый в квадрат.
Пример 5. Представить одночлен 121a6 в виде одночлена, возведённого в квадрат.
Попробуем найти произведение, которое во второй степени будет равно выражению 121a6.
Прежде всего заметим, что число 121 получается, если число 11 возвести в квадрат. То есть первый сомножитель будущего произведения мы нашли. А степень a6 получается в том случае, если возвести в квадрат степень a3. Значит вторым сомножителем будущего произведения будет a3.
Таким образом, если произведение 11a3 возвести во вторую степень, то получится 121a6
(11a3)2 = 112 × (a3)2 = 121a6
Значит, 121a6 = (11a3)2. Выражение (11a3)2 это и есть одночлен, возведённый в квадрат.
Разложение одночлена на множители
Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.
Пример 1. Разложить одночлен 3a3b2 на множители
Данный одночлен можно разложить на множители 3, a, a, a, b, b
3a3b2 = 3aaabb
Либо степень b2 можно не раскладывать на множители b и b
3a3b2 = 3aaab2
Либо степень b2 разложить на множители b и b, а степень a3 оставить без изменений
3a3b2 = 3a3bb
В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.
Пример 2. Разложить одночлен 10a2b3c4 на множители.
Разложим коэффициент 10 на множители 2 и 5, степень a2 разложим на множители aa, степень b3 — на множители bbb, степень c4 — на множители cccc
10a2b3c4 = 2 × 5 × aabbbcccc
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Периметр, площадь и объём
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
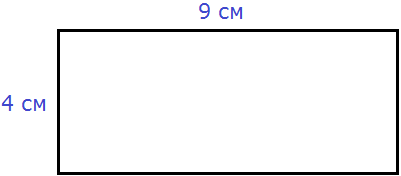
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
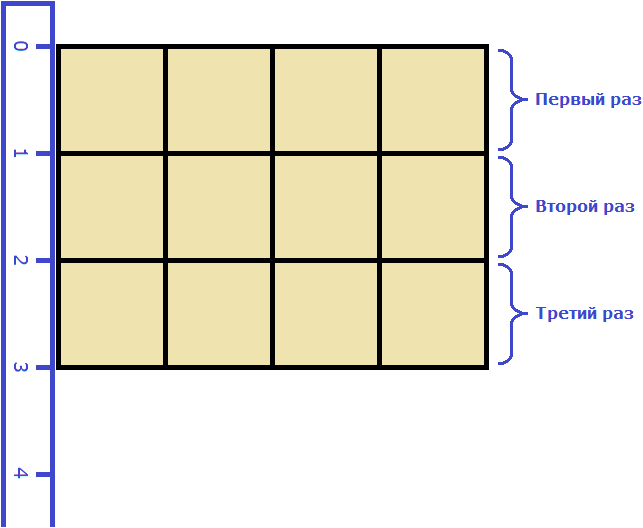
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
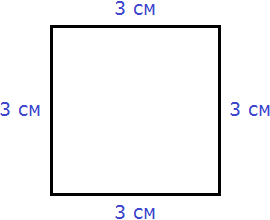
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
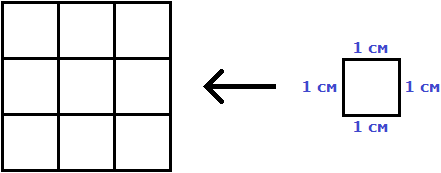
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
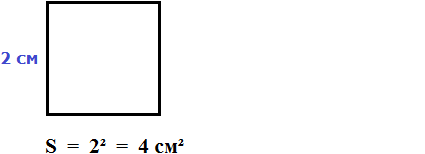
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
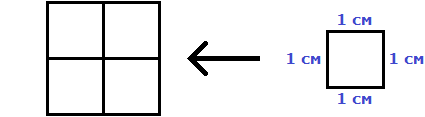
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
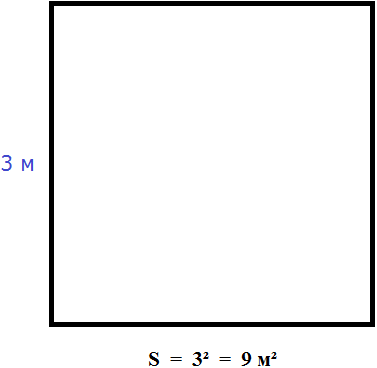
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
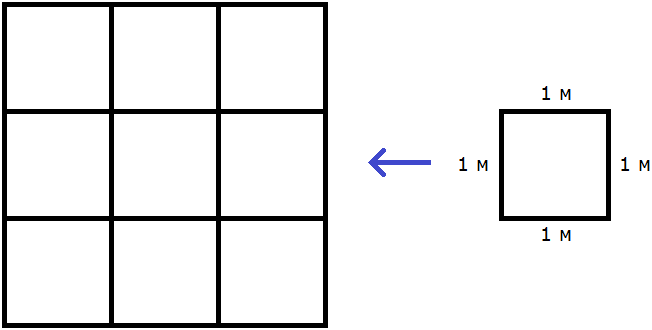
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
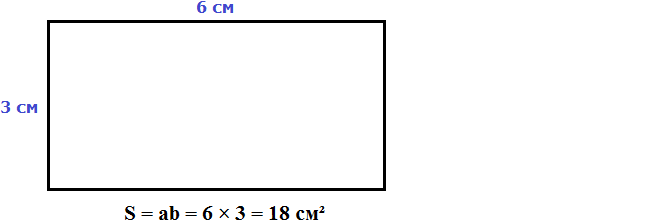
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
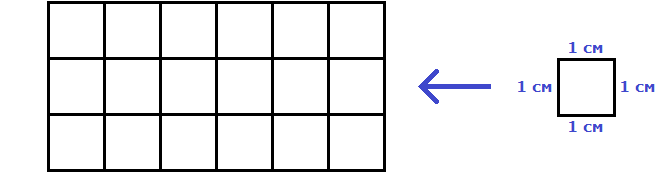
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
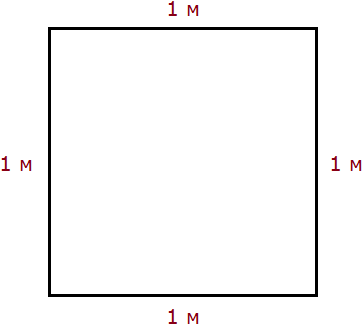
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
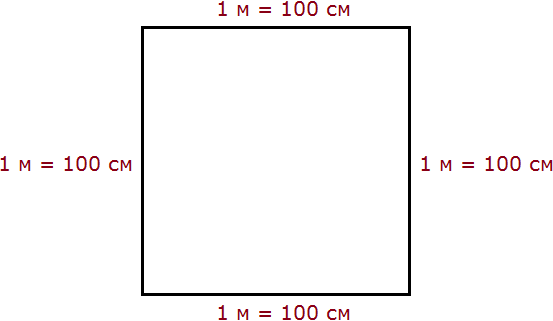
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
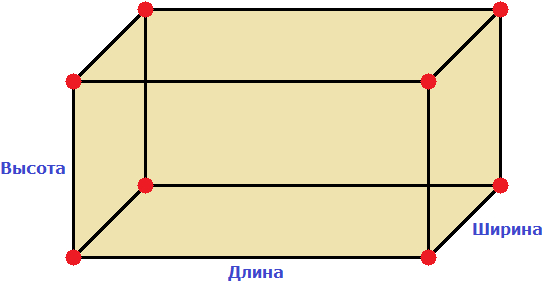
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
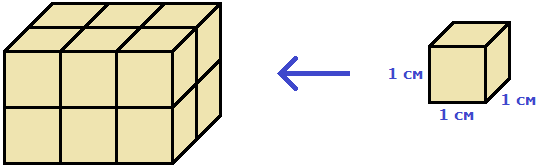
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
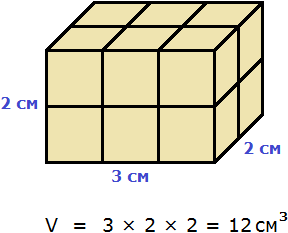
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
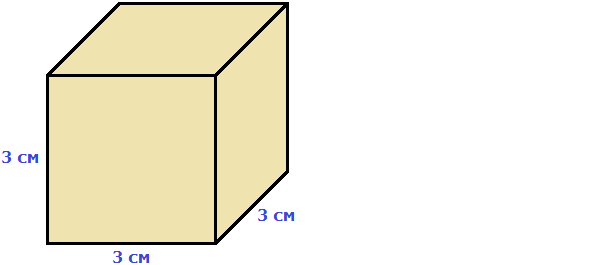
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
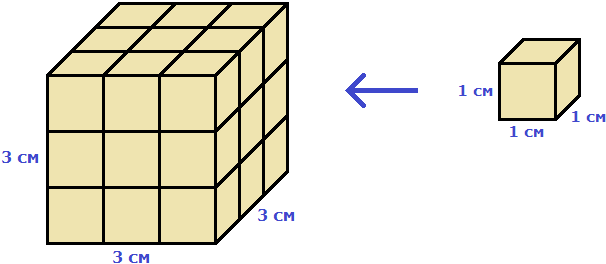
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
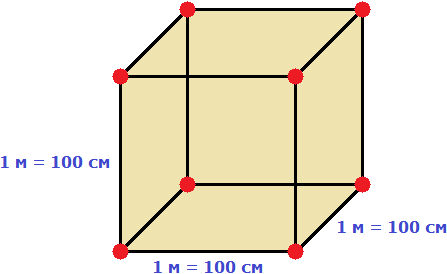
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
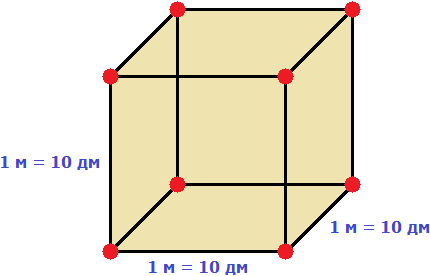
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
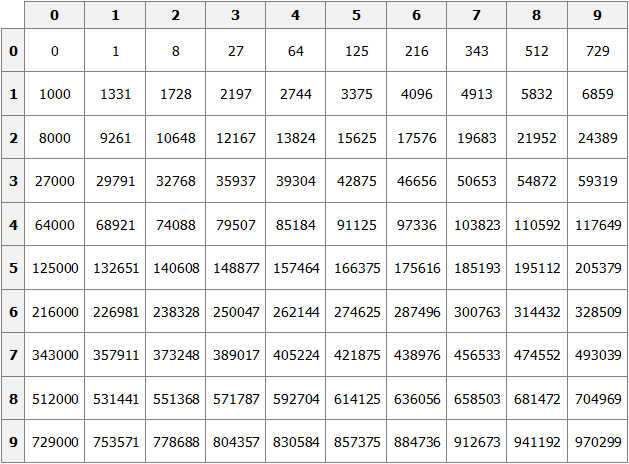
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
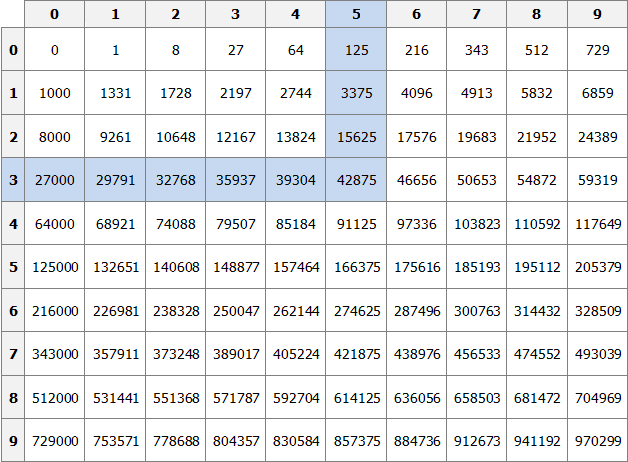
353 = 42875
Задания для самостоятельного решения
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
 длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.Решение
a — длина
b — ширина
c — высота
a = 42 м
b = 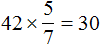 м
м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
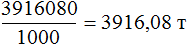
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Степень с целым показателем
Степень с целым показателем — это степень, показателем которой является любое целое число.
В прошлом уроке мы изучили степень с натуральным показателем. Этот вид степени тоже является степенью с целым показателем, поскольку натуральные числа относятся к целым числам.
Также, мы рассмотрели степень, показателем которой является 0. Этот вид степени тоже является степенью с целым показателем, поскольку 0 относится к целым числам.
Рассмотрим ещё один вид степени с целым показателем, а именно показателем которой является целое отрицательное число. Выглядят эти степени так:
2−2, 10−7, a−8
В дальнейшем любую степень с натуральным, нулевым или целым отрицательным показателем, мы будем называть степенью с целым показателем.
Правило вычисления
Рассмотрим следующую последовательность степеней:
20, 21, 22, 23, 24, 25
Первая степень в этой последовательности это степень 20. Предыдущая степень с целым показателем будет уже с отрицательным показателем и выглядеть как 2−1.
2−1, 20, 21, 22, 23, 24, 25
А предыдущая степень с целым показателем, которая располагается до 2−1, будет степень 2−2
2−2, 2−1, 20, 21, 22, 23, 24, 25
Продолжим эту последовательность в сторону степеней с целыми отрицательными показателями:
2−5, 2−4, 2−3, 2−2, 2−1, 20, 21, 22, 23, 24, 25
Теперь попробуем вычислить эти степени. Степени с натуральными показателями и степень, показателем которой является 0, вычисляются легко:
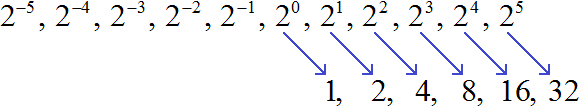
А как вычислить степени с отрицательными показателями? Для начала немного отойдём от темы и затронем несколько закономерностей.
В отрицательную степень число возводится немного иначе. Следует понимать, что если при возведении в положительную степень число увеличивается, то при возведении в отрицательную степень это число наоборот уменьшается.
Если мы возьмём какое-нибудь число n, и начнём последовательно увеличивать его степень, то получим последовательность чисел, в которой каждое число меньше следующего в n раз.
Например, возьмём число 2. Начиная с нуля будем последовательно увеличивать его показатель:
20, 21, 22, 23, 24, 25
Вычислим эти степени:
1, 2, 4, 8, 16, 32
Получили последовательность чисел, в которой каждое число меньше следующего числа в 2 раза. Тогда логично предположить, что число, располагающееся до единицы, будет в два раза меньше единицы. Его можно получить, если 1 разделить на 2
![]()
Вернёмся к нашей исходной последовательности, где мы вычисляли степени. Получается, что степень 2−1 мы вычислили. Она равна рациональному числу ![]()
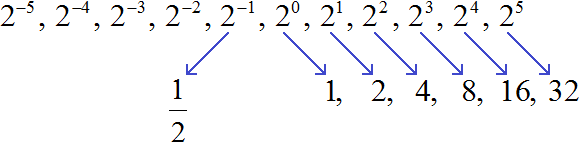
Предыдущее за числом ![]() должно быть в два раза меньше, чем
должно быть в два раза меньше, чем ![]() . Чтобы его получить разделим
. Чтобы его получить разделим ![]() на 2
на 2
![]()
Получили ![]() . Это значение степени 2−2
. Это значение степени 2−2
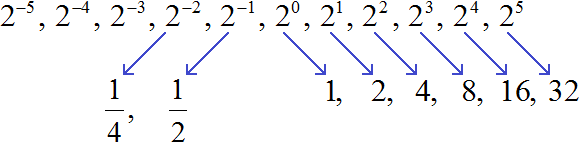
Продолжая деление на 2 можно получить значения остальных степеней с целыми отрицательными показателями:
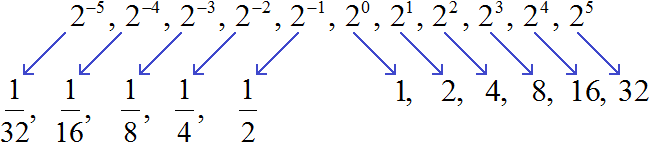
Заметим, что в данной последовательности значения степеней с отрицательными показателями являются обратными числами к значениям степеней с натуральными показателями:
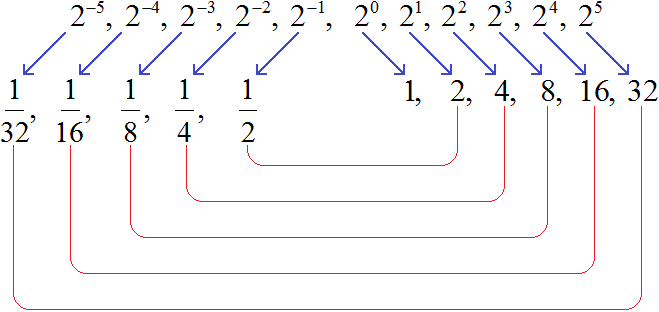
К примеру, значение степени в 22 есть число 4. А значение степени 2−2 есть число ![]() . Числа 4 и
. Числа 4 и ![]() являются обратными друг другу. А степени 22 и 2−2 отличаются только тем, что у них противоположные показатели.
являются обратными друг другу. А степени 22 и 2−2 отличаются только тем, что у них противоположные показатели.
Можно сделать вывод, что для вычисления степени с отрицательным показателем, нужно записать дробь, в числителе которой единица, а в знаменателе та же самая степень, но с противоположным показателем. Покажем это на примере степени 2−2
![]()
Вычислим степень, находящуюся в знаменателе:
![]()
Таким образом, чтобы вычислить степень вида a−n можно воспользоваться следующим правилом:
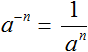
Данное правило можно доказать, используя правило деления степеней с одинаковыми основаниями. Допустим, потребовалось вычислить выражение 23 : 25. Запишем это деление в виде дроби
![]()
Воспользуемся правилом деления степеней с одинаковыми основаниями:
![]()
Получили степень с отрицательным показателем 2−2. Ранее мы выяснили, что её значение равно ![]() . Чтобы убедиться в этом, попробуем вычислить выражение
. Чтобы убедиться в этом, попробуем вычислить выражение ![]() как обычно, не используя правило деления степеней:
как обычно, не используя правило деления степеней:
![]()
Получили рациональное число ![]() . Сократим его на 8. Тогда получим
. Сократим его на 8. Тогда получим ![]()
![]()
Пример 2. Найти значение выражения 9−2
Воспользуемся правилом вычисления степени с целым отрицательным показателем:
![]()
Пример 3. Найти значение выражения 3−3
![]()
Следует упомянуть, что правило работает только тогда, когда a ≠ 0.
Действительно, если a будет равным нулю, то в знаменателе получим 0, а на нуль делить нельзя.
Пример 4. Найти значение выражения ![]()
Пример 5. Найти значение выражения 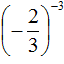
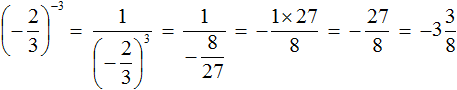
При возведении обыкновенных дробей в отрицательную степень, можно пользоваться формулой 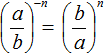 . Решим предыдущие два примера с помощью этой формулы:
. Решим предыдущие два примера с помощью этой формулы:
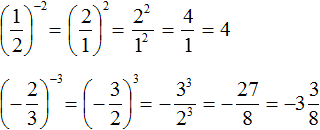
Желательно уметь возводить обыкновенную дробь в отрицательную степень как с помощью формулы, так и без неё.
Тождественные преобразования
Все тождественные преобразования, которые мы рассматривали при изучении степени с натуральным показателем, сохраняются и для степеней с целыми отрицательными показателями.
Например, чтобы представить выражение 2−1 × 2−3 в виде степени, можно воспользоваться основным свойством степени:
2−1 × 2−3 = 2−1 + (−3) = 2−4
Пример 2. Найти значение выражения 5−15 × 516
Воспользуемся основным свойством степени:
5−15 × 516 = 5−15 + 16 = 51 = 5
или:
![]()
Видим, что первый вариант решения намного проще и удобнее.
Пример 3. Найти значение выражения (10−4)−1
Воспользуемся правилом возведения степени в степень:
(10−4)−1 = 10−4 × (−1) = 104 = 10000
Пример 4. Найти значение выражения ![]()
Представим число основание 10 в виде произведения 2 × 5. Тогда числитель примет вид (2 × 5)−6
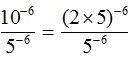
В числителе применим правило возведения в степень произведения:
![]()
Сократим получившуюся дробь на 5−6
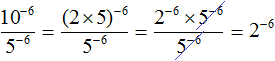
Вычислим степень 2−6
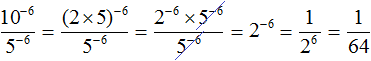
Поднятие степени из знаменателя в числитель и наоборот
Если знаменатель дробного выражения содержит степень, то данную степень можно поднять в числитель, изменив знак показателя этой степени на противоположный. Значение выражения при этом не меняется. Данное преобразование иногда используется при упрощении выражений.
Рассмотрим следующее равенство:
![]()
Данное равенство является верным, поскольку выражение ![]() равно 20, а любое число в нулевой степени есть единица.
равно 20, а любое число в нулевой степени есть единица.
Попробуем поднять степень 22 из знаменателя в числитель, изменив знак показателя этой степени на противоположный. При этом, поднятую степень и ту степень, которая располагалась в числителе, соединим знаком умножения:
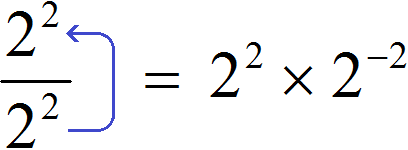
Получили выражение 22 × 2−2. Чтобы его вычислить, воспользуемся основным свойством степени:
22 × 2−2 = 22 + (−2) = 20 = 1
Получился тот же результат, что и раньше. Значит значение выражения не изменилось. Как это работает?
Если в равенстве поменять местами левую и правую часть, то получим равенство
![]() . Это позволяет заменять в выражениях дробь вида
. Это позволяет заменять в выражениях дробь вида ![]() на тождественно равное ей выражение a−n.
на тождественно равное ей выражение a−n.
Теперь представим выражение ![]() в виде произведения
в виде произведения ![]() . То есть заменим деление умножением. Напомним, что при замене деления умножением, делимое умножают на число, обратное делителю. А обратное делителю число в данном случае это дробь
. То есть заменим деление умножением. Напомним, что при замене деления умножением, делимое умножают на число, обратное делителю. А обратное делителю число в данном случае это дробь ![]()
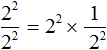
Теперь воспользуемся правилом ![]() . В произведении
. В произведении ![]() заменим дробь
заменим дробь ![]() на тождественно равное ей выражение 2−2
на тождественно равное ей выражение 2−2
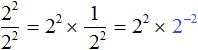
Далее, как и раньше применяем основное свойство степени:
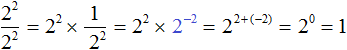
Получился тот же результат 1.
Таким же образом можно опустить степень из числителя в знаменатель, изменив знак показателя этой степени на противоположный.
Рассмотрим выражение ![]() . Чтобы найти его значение, воспользуемся правилом деления степеней с одинаковыми основаниями. В результате получим
. Чтобы найти его значение, воспользуемся правилом деления степеней с одинаковыми основаниями. В результате получим ![]()
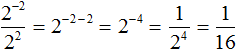
Теперь попробуем решить этот пример, опустив степень 2−2 из числителя в знаменатель, изменив знак показателя этой степени на противоположный. При этом, опущенную степень 2−2 и ту степень, которая располагалась в знаменателе, соединим знаком умножения. А в числителе останется единица:
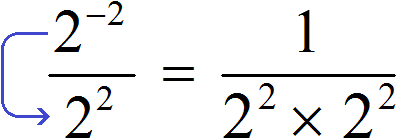
Дальнейшее вычисление не составит особого труда:
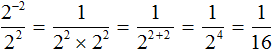
Как и в прошлом примере выражение ![]() представимо в виде произведения
представимо в виде произведения ![]()
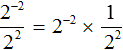
Этим и объясняется появление единицы в числителе, после того как степень 2−2 была опущена в знаменатель.
Переносимых в знаменатель либо в числитель степеней может быть несколько. Например, знаменатель дроби ![]() содержит степени 32, a3, b4. Перенесём эти степени в числитель, изменив знаки их показателей на противоположные. В результате получим выражение 3−2a−3b−4.
содержит степени 32, a3, b4. Перенесём эти степени в числитель, изменив знаки их показателей на противоположные. В результате получим выражение 3−2a−3b−4.
Пример 2. Поднять степени из знаменателя дроби ![]() в числитель
в числитель
![]()
Пример 3. Поднять степени из знаменателя дроби ![]() в числитель
в числитель
![]()
Пример 4. Поднять степень из знаменателя дроби ![]() в числитель
в числитель
![]()
Пример 5. Опустить степень из числителя дроби ![]() в знаменатель
в знаменатель
![]()
Пример 6. Степень из числителя дроби ![]() опустить в знаменатель, а степень из знаменателя поднять в числитель
опустить в знаменатель, а степень из знаменателя поднять в числитель
![]()
Представлять дробь ![]() в виде произведения
в виде произведения ![]() вовсе не обязательно. Если пропустить эту запись, то данный пример можно решить короче:
вовсе не обязательно. Если пропустить эту запись, то данный пример можно решить короче:
![]()
Пример 7. В дроби 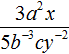 перенести из знаменателя в числитель только те степени, которые имеют отрицательные показатели:
перенести из знаменателя в числитель только те степени, которые имеют отрицательные показатели:
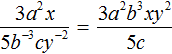
Пример 8. Представить произведение 3x−5 в виде дроби, не содержащей степени с отрицательным показателем.
Перепишем произведение 3x−5 с помощью знака умножения:
3 × x−5
Сомножитель 3 оставим без изменений, а сомножитель x−5 заменим на тождественно равную ему дробь ![]()
![]()
Теперь согласно правилу умножения целого числа на дробь, умножим множитель 3 на числитель дроби ![]() . В результате образуется дробь
. В результате образуется дробь ![]()
![]()
Пример 9. Представить произведение 3(x + y)−4 в виде дроби, не содержащей степени с отрицательным показателем.
Выражение состоит из сомножителей 3 и (x + y)−4. Сомножитель 3 оставим без изменений, а сомножитель (x + y)−4 заменим на тождественно равную ему дробь ![]()
![]()
Теперь умножим множитель 3 на числитель дроби ![]() . В результате образуется дробь
. В результате образуется дробь ![]()
![]()
Пример 10. Представить дробь ![]() в виде произведения.
в виде произведения.
Чтобы решить этот пример, достаточно поднять степень x2 в числитель, изменив знак показателя этой степени на противоположный:
![]()
Как и в прошлых примерах дробь ![]() можно было представить в виде произведения
можно было представить в виде произведения ![]() . Затем воспользовавшись правилом
. Затем воспользовавшись правилом ![]() , заменить сомножитель
, заменить сомножитель ![]() на тождественно равный ему сомножитель x−2.
на тождественно равный ему сомножитель x−2.
![]()
Пример 11. Представить дробь 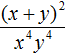 в виде произведения.
в виде произведения.
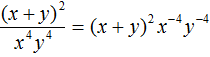
Пример 12. Найти значение выражения 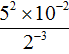
Поднимем степень 2−3 из знаменателя в числитель, а степень 10−2 из числителя опустим в знаменатель:
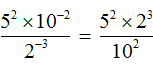
Вычислим значения степеней, содержащихся в числителе и в знаменателе:
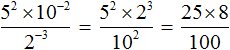
Сократим полученную дробь на 25. Тогда останется дробь , значение которой равно 2.
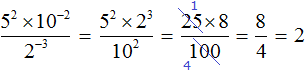
А если бы мы не подняли степень 2−3 в числитель, и степень 10−2 не опустили в знаменатель, а стали вычислять каждую степень по отдельности, то получили бы не очень компактное решение:
Возведение числа 10 в целую отрицательную степень
Число 10 в отрицательную степень возводится таким же образом, как и другие числа. Например:
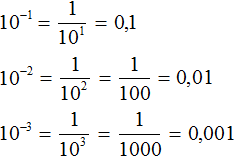
Замечаем, что количество нулей, которые получаются в ответе равны модулю показателя исходной степени. Например, в степени 10−2 модуль показателя равен 2. Это значит, что в ответе будет содержаться два нуля. Так оно и есть:
![]()
Чтобы возвести число 10 в отрицательную степень, нужно перед единицей записать количество нулей, равное модулю показателя исходной степени.
При этом после первого нуля следует поставить запятую. Примеры:
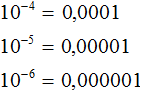
Представление чисел 0,1, 0,01, 0,001 в виде степени с основанием 10
Чтобы представить числа 0,1, 0,01, 0,001 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать отрицательный показатель, модуль которого равен количеству нулей исходного числа.
Представим число 0,1 в виде степени с основанием 10. Видим, что в числе 0,1 один нуль. Значит, число 0,1 в виде степени с основанием 10 будет представлено как 10−1. Показатель степени 10−1 равен −1. Модуль этого показателя равен количеству нулей в числе 0,1
0,1 = 10−1
Число 0,1 это результат деления ![]() , а эта дробь есть значение степени 10−1.
, а эта дробь есть значение степени 10−1.
Пример 2. Представить число 0,01 в виде степени с основанием 10.
В числе 0,01 два нуля. Значит, число 0,01 в виде степени с основанием 10 будет представлено как 10−2. Показатель степени 10−2 равен −2. Модуль этого показателя равен количеству нулей в числе 0,01
0,01 = 10−2
Число 0,01 это результат деления ![]() , то есть
, то есть ![]() , а эта дробь есть значение степени 10−2.
, а эта дробь есть значение степени 10−2.
Пример 3. Представить число 0,001 в виде степени с основанием 10.
0,001 = 10−3
Пример 4. Представить число 0,0001 в виде степени с основанием 10.
0,0001 = 10−4
Пример 5. Представить число 0,00001 в виде степени с основанием 10.
0,00001 = 10−5
Стандартный вид числа
Запишем число 2 000 000 в виде произведения числа 2 и 1 000 000
2 × 1 000 000
Сомножитель 1 000 000 можно заменить на степень 106
2 × 106
Такой вид записи называют стандартным видом числа. Стандартный вид числа позволяет записывать в компактном виде как большие, так и маленькие числа.
Например, маленькое число 0,005 можно записать в виде произведения числа 5 и десятичной дроби 0,001.
5 × 0,001
Десятичную дробь 0,001 можно заменить на степень с 10−3
5 × 10−3
Значит, число 0,005 в стандартном виде будет выглядеть как 5 × 10−3
0,005 = 5 × 10−3
По стандартному виду числа можно вычислить изначальное число. Так, при записи числа 2 000 000 в стандартном виде, мы получили произведение 2 × 106. Если вычислить это произведение, то снова получим 2 000 000
2 × 106 = 2 × 1 000 000 = 2 000 000
А при записи числа 0,005 в стандартном виде мы получили произведение 5 × 10−3. Если вычислить это произведение, то получим 0,005
![]()
То есть записывая число в стандартном виде нужно записывать его так, чтобы сохранить его изначальное значение.
Стандартным видом числа называют запись вида a × 10n, где 1 ≤ a < 10 и n — целое число.
Число а это исходное число, которое надо записать в стандартном виде. Оно должно удовлетворять неравенству 1 ≤ a < 10. Чаще всего исходное число надо приводить к виду, при котором неравенство 1 ≤ a < 10 становится верным.
Например, представим число 12 в стандартном виде. Для начала проверим становится ли верным неравенство 1 ≤ a < 10 при подстановке числа 12 вместо а
1 ≤ 12 < 10
Неравенство верным не становится. Чтобы сделать неравенство верным, приведём число 12 к виду, при котором оно удовлетворяло бы данному неравенству. Для этого передвинем в числе 12 запятую влево на одну цифру:
1,2
Число 12 обратилось в число 1,2. Это число будет удовлетворять неравенству 1 ≤ a < 10
1 ≤ 1,2 < 10
Теперь наша задача состоит в том, чтобы записать произведение a × 10n. С числом а мы разобрались — этим числом у нас будет 1,2. А как подобрать степень с основанием 10?
После переноса запятой на одну цифру влево, число 12 утратило своё изначальное значение. Запятая на одну цифру влево двигается тогда, когда число делят на 10. А чтобы восстановить изначальное значение числа запятую нужно передвинуть обратно в правую сторону на одну цифру, то есть умножить число 1,2 на 10.
Значит, чтобы записать число 12 в стандартном виде, нужно представить его в виде произведения 1,2 × 10¹
12 = 1,2 × 10¹
Пример 2. Записать число 0,5 в стандартном виде.
Число 0,5 не удовлетворяет неравенству 1 ≤ a< 10, поэтому передвинем запятую в этом числе на одну цифру вправо. В результате получим число 5, которое удовлетворяет неравенству 1 ≤ a< 10.
Теперь запишем произведение вида a × 10n. Число a в данном случае это 5. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10n стало равным числу 0,5. Число 0,5 получится если умножить число 5 на множитель 0,1, который представим в виде степени 10−1. В результате получим следующую запись:
0,5 = 5 × 10−1
Пример 3. Записать число 652 000 в стандартном виде.
Число 652 000 не удовлетворяет неравенству 1 ≤ a< 10, поэтому передвинем запятую в этом числе на пять цифр влево. В результате получим число 6,52000 которое удовлетворяет неравенству 1 ≤ a< 10.
Теперь запишем произведение вида a × 10n. Число a в данном случае это 6,52000. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10n стало равным числу 652 000. Число 652 000 получится если число 6,52000 умножить на 100 000, а это есть степень 105. В результате получим следующую запись:
652 000 = 6,52000 × 105
Нули в конце десятичной дроби 6,52000 можно отбросить. Тогда получим более компактную запись:
652 000 = 6,52 × 105
Пример 5. Записать число 1 024 000 в стандартном виде.
Число 1 024 000 не удовлетворяет неравенству 1 ≤ a< 10, поэтому передвинем запятую в этом числе на шесть цифр влево. В результате получим число 1,024000 которое удовлетворяет неравенству 1 ≤ a< 10.
Теперь запишем произведение вида a × 10n. Число a в данном случае это 1,024000 . А степень с основанием 10 надо выбрать так, чтобы произведение a × 10n было равно изначальному числу 1 024 000. Число 1 024 000 получится если число 1,024000 умножить на 1 000 000, а это есть степень 106. В результате получим следующую запись:
1 024 000 = 1,024000 × 106
Нули в конце десятичной дроби 1,024000 можно отбросить:
1 024 000 = 1,024 × 106
Отбрасывать можно только те нули, которые располагаются в конце, и после которых нет других цифр, бóльших нуля. В приведённом примере были отброшены только три нуля, а нуль располагавшийся между запятой и цифрой 2 был сохранен, несмотря на то, что он тоже располагался после запятой.
Пример 6. Записать число 0,000325 в стандартном виде.
Передвинем в данном числе запятую так, чтобы оно удовлетворяло неравенству 1 ≤ a< 10. В результате получим число 3,25
Теперь запишем произведение вида a × 10n. Число a в данном случае это 3,25. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10n было равно изначальному числу 0,000325. Число 0,000325 получится если число 3,25 умножить на множитель 0,0001 который представим в виде степени 10−4. В результате получим следующую запись:
0,000325 = 3,25 × 10−4
Задания для самостоятельного решения

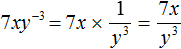
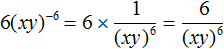


Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
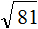


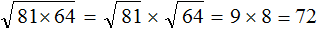
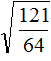
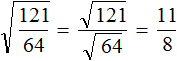
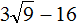

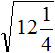
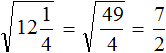
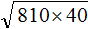
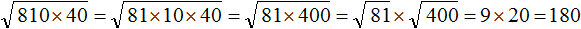
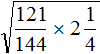
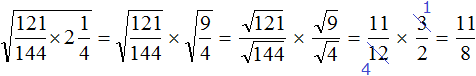
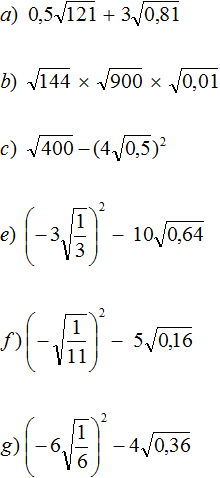
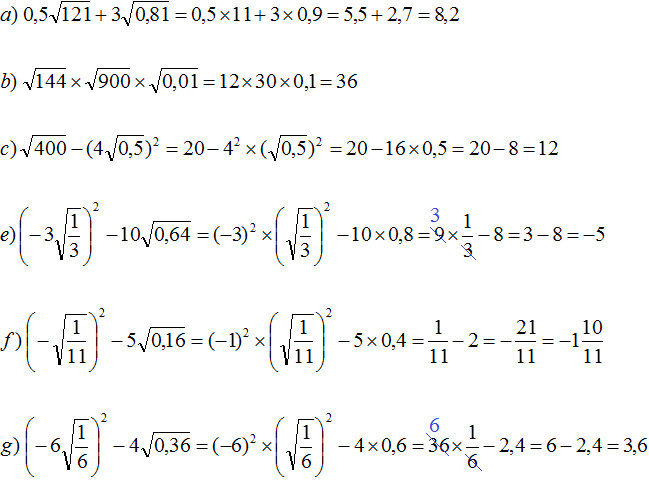
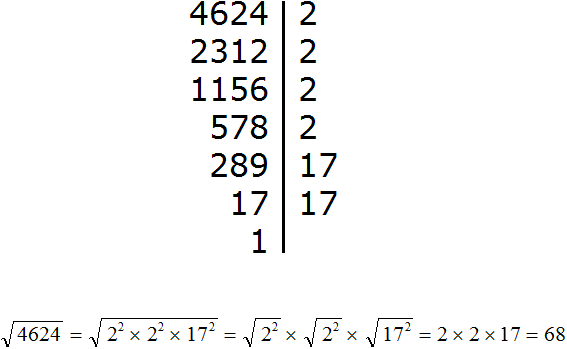

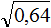

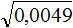

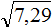

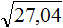
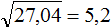
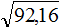
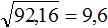
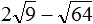
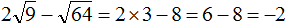
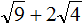
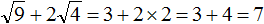


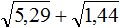





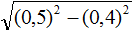
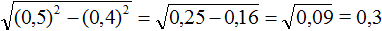
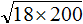
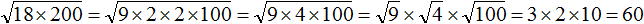
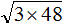

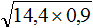
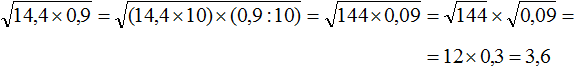
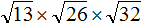

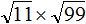



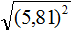

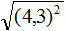

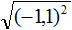
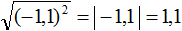

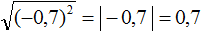

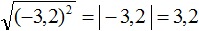

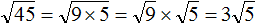
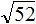

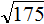
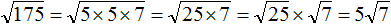
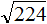
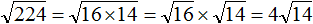
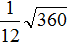

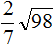
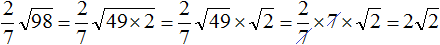
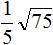



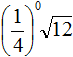

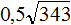


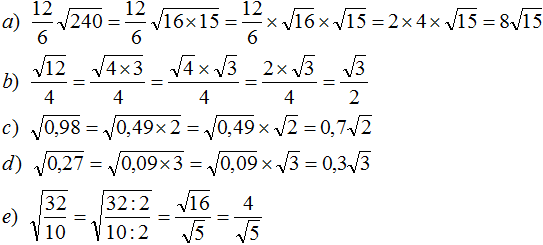
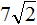

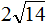
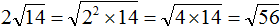

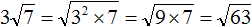
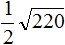
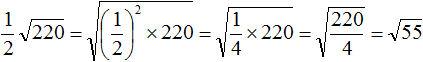
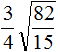
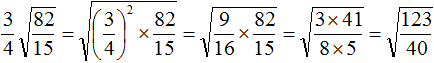
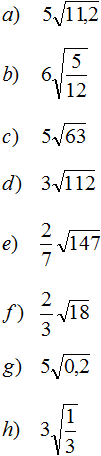


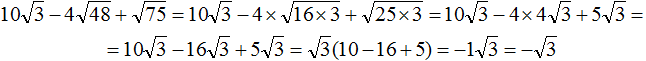




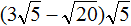

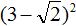


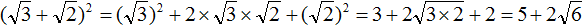

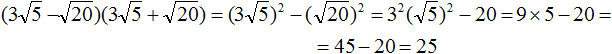
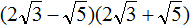
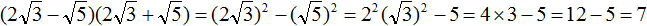
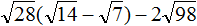

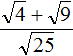
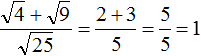
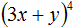
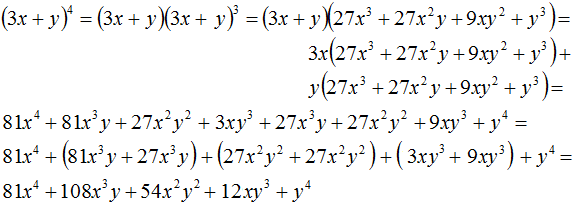
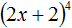
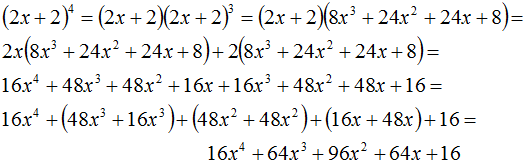
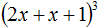
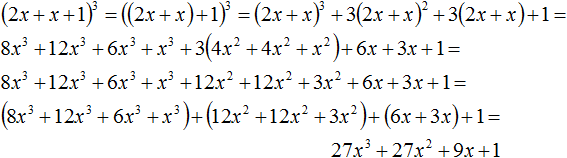
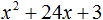
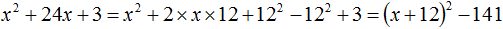
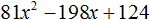
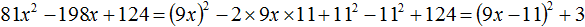
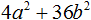
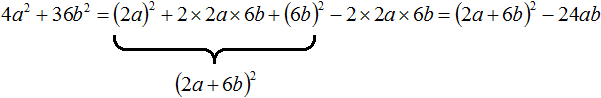
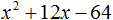
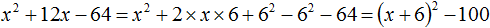
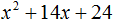
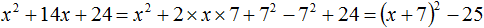
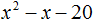
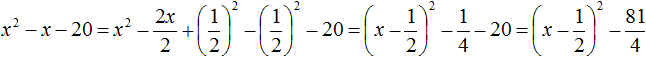
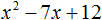
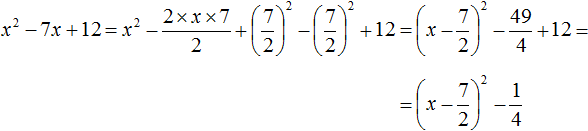
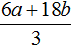
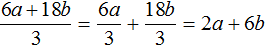
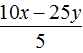
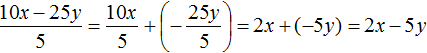
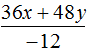
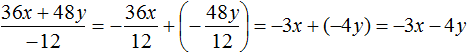
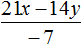
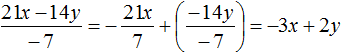
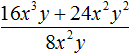
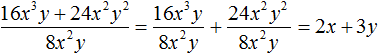
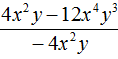
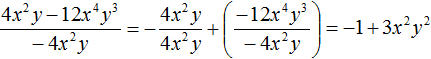
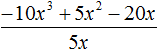
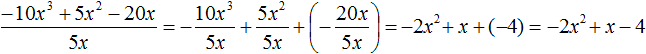
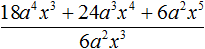
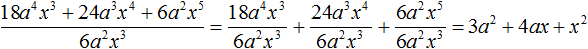
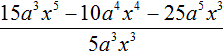
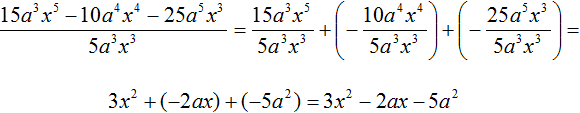
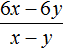
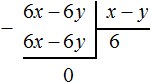
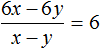
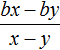
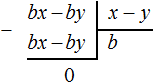
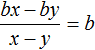
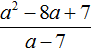
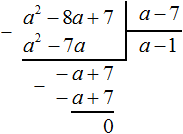
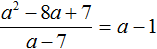
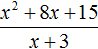
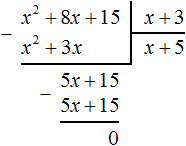
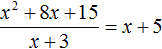
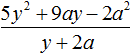
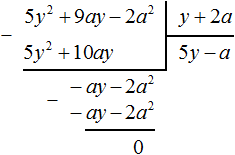
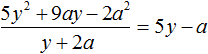
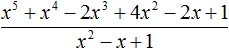
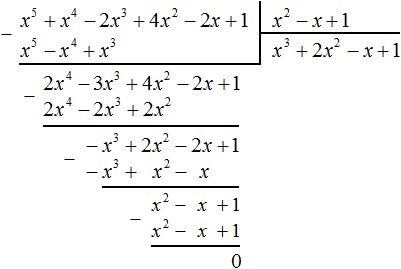
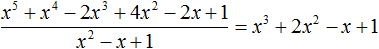
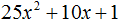
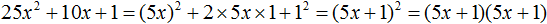
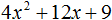
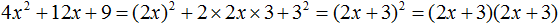

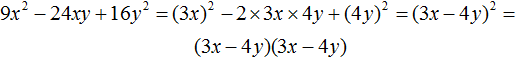
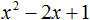
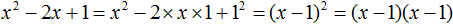
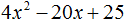
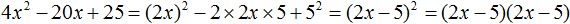


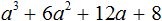
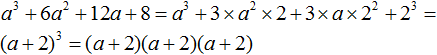
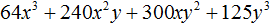
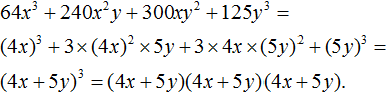
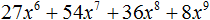
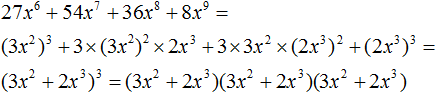

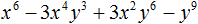
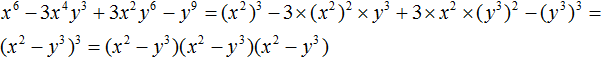
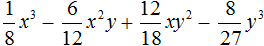
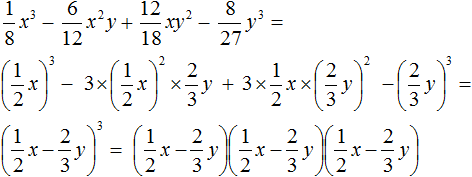

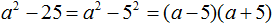
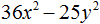
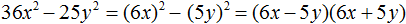
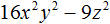
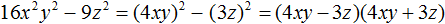
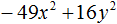
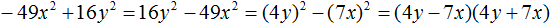

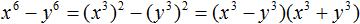
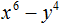
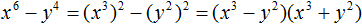

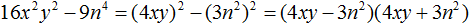
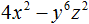
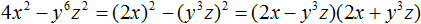
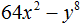
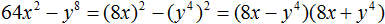
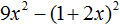
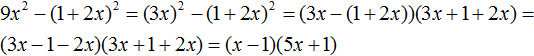


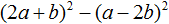



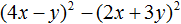
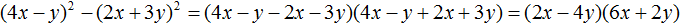
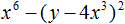

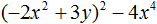
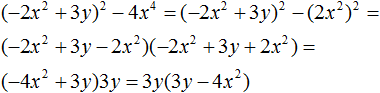



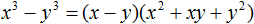
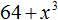
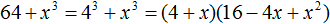
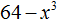

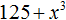
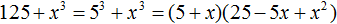
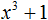


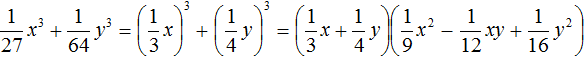
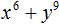
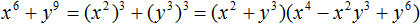


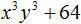
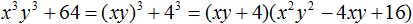
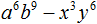
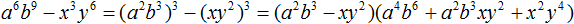
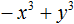
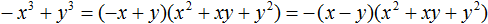
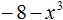
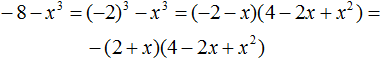

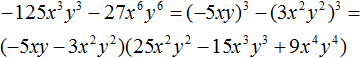
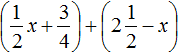
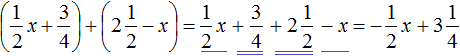
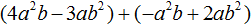
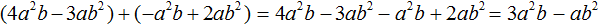
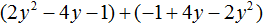

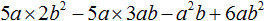
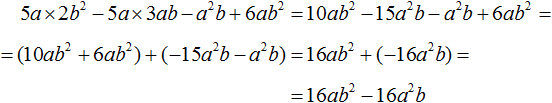
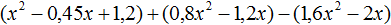
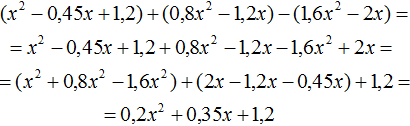

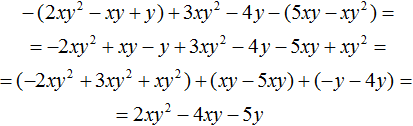
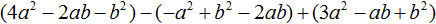
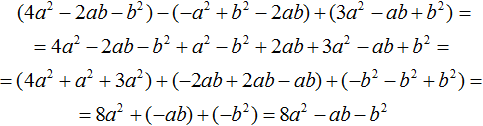
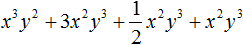
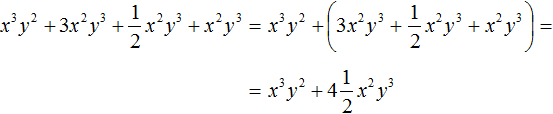
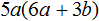
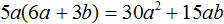
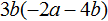
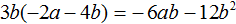



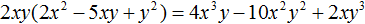
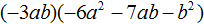


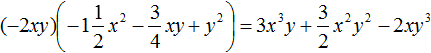


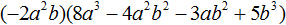
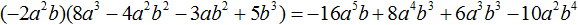

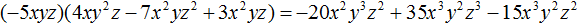


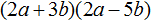


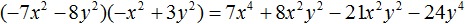

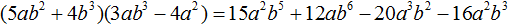
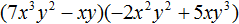
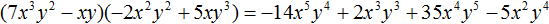
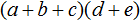
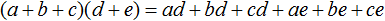
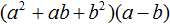
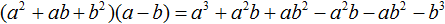
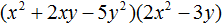

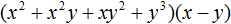
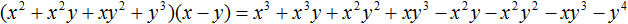
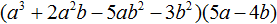



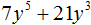
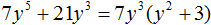
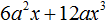
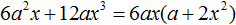
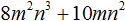
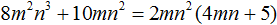
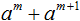


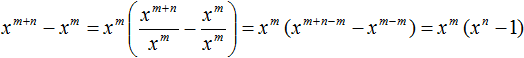

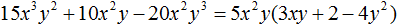
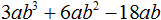
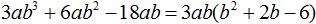
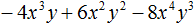
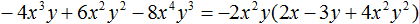
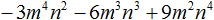
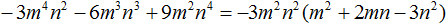
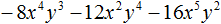
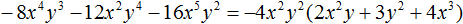
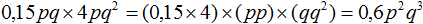
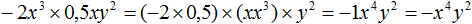

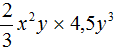 к стандартному виду.
к стандартному виду.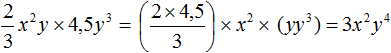
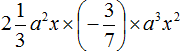 к стандартному виду.
к стандартному виду.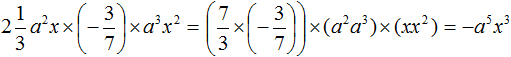
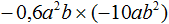

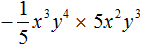
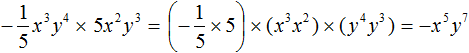
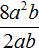
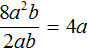
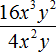
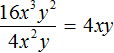
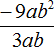

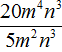
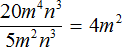
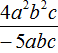
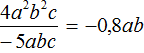
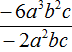
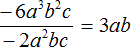
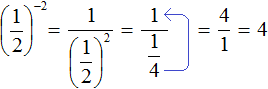
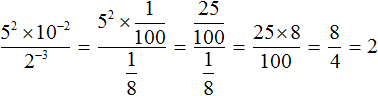




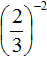

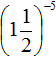



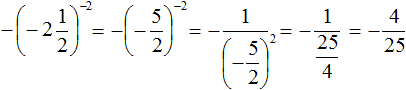
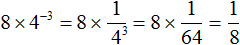

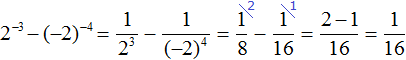
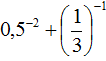
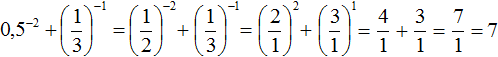
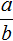 в виде произведения.
в виде произведения.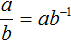
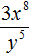 в виде произведения.
в виде произведения.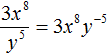
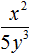 в виде произведения.
в виде произведения.
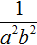 в виде произведения.
в виде произведения.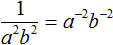
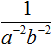 в виде произведения.
в виде произведения.
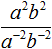 в виде произведения.
в виде произведения.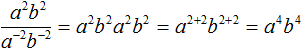
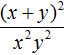 в виде произведения.
в виде произведения.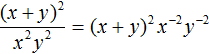
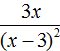 в виде произведения.
в виде произведения.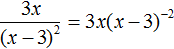
 в виде произведения.
в виде произведения.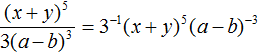
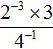 .
.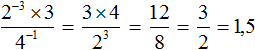
 .
.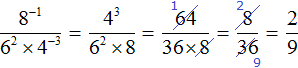
 .
.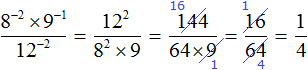
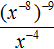 .
.
 .
.
 .
.
 .
.