Если из обеих частей уравнения извлечь квадратный корень, то полýчится уравнение равносильное исходному.
Рассмотрим следующее уравнение:
x2 = 16
Это простейшее квадратное уравнение, имеющее два корня: 4 и −4. Такое уравнение мы решали используя определение квадратного корня.
Согласно определению квадратного корня, число b является квадратным корнем из числа a, если b2 = a и обозначается как b = √a.
Тогда в случае x2 = 16, можно записать что x = √16, откуда x = ±4.
Теперь решим данное квадратное уравнение путем извлечения квадратного корня из обеих частей уравнения.
“Обернём” обе части уравнения x2 = 16 в квадратный корень:
![]()
Теперь вспоминаем одно из свойств квадратного корня, которое гласит что квадратный корень из квадрата числа равен модулю этого числа
![]()
Тогда в левой части нашего уравнения получим модуль из x, а в правой части число 4
![]()
Получили простейшее уравнение с модулем. Оно имеет два корня: 4 и −4. Запишем это решение в виде совокупности уравнений:
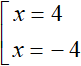
Проверка:
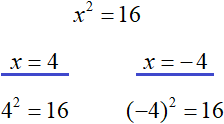
Из правой части уравнения x2 = 16 следует извлекать именно арифметический квадратный корень. Ранее мы говорили, что квадратный корень имеет два значения: положительное и отрицательное. То есть:
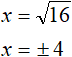
Но в данном случае нас интересует именно неотрицательное значение 4 (его и называют арифметическим квадратным корнем). Потому что если мы извлечем и второй корень (отрицательный −4), то получим уравнение |x|= −4 которое не имеет решений.
Пример 2. Решить уравнение 3x2 = 12
Решение
Разделим обе части на 3
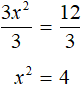
Извлечём квадратный корень из обеих частей получившегося уравнения:
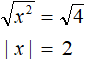
Получили простейшее уравнение с модулем. Решим его, сведя в совокупность:
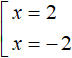
Ответ: 2 и −2.
Пример 3. Решить уравнение (x + 2)2 = 25
Решение
Извлечём квадратный корень из обеих частей получившегося уравнения:

Решим получившееся уравнение с модулем:
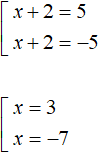
Ответ: 3 и −7.
Пример 4. Решить уравнение x2 − 10 = 39
Решение
Перенесем −10 в правую часть изменив знак:
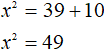
Извлечём квадратный корень из обеих частей получившегося уравнения:
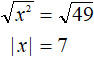
Решим получившееся уравнение с модулем:
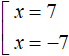
Ответ: 7 и −7.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
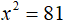
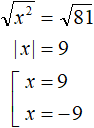
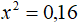
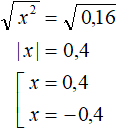
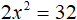
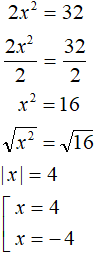
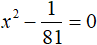
 и
и  .
.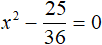
 и
и  .
.
ураа
дааа урааа новаааяяя тееемааа
Спасибо, я обязательно должен дойти до нужного мне уровня знаний в данном придмете!
Здравствуйте . Все темы здесь до 8 класса . Потом будут до 11 класса ?
ia tak sebe znal matematiku tablicu umnojenia tolko… na etom prikrasnom saite viuchil poshagovuiu matematuku, i ochen ponravilos eti 75 shagov! posle etoi infarmacii chto tut vilojena na saite.viuchil vse 75shagov i vaznikla problema,dalshe zatrudnilsia neznaiu chto sledovatelno viuchit,prochest, chtobi poluchilos kak bi prodoljenie uchenia matematiki.chtobi poiti v period i,progresirovat dalshe,kak bi ot punkta A doiti do punkta Я. tak skazat ot a do Я.i td… chto viuchit?kakoi knigoi zaminit, chtobi poiti dalshe k sojaleniu neznaiu. chtobi poluchilosbi tipo kak bi prodoljenie.v etoi teme kto kompeten i znatok matematiki pomogite otvetom chem prodoljit? bolshoe spasibo…
Здравствуйте, у вас есть урок тождественные преобразования дробно-рациональных выражений?
chto eto takoe pojalusto prosveti?podskaji v kakix sluchaiax drobi preobrozuiutsa?
Посоветуйте учебники по алгебре 7-9 классов
да любой берете, по алгебре они одинаковы все , это же не история с разными интерпретациями
Макарычев, мерзляк
спасибо я очень благодарен вам
потому что при ваши помощи я поступил в универ , вы дали мне хороши толчок до алгебры )
сейчас я в 1 курсе но Алгебра всё ещё нужна, можете посоветовать учебники для самостоятельного изучения от 9 до 11 класса?
я готовлюсь к егэ и пока нахожусь только на 12 шаге с дробями. поэтому мне интересно, достаточно ли сейчас на сайте опубликовано шагов для подготовки к егэ по профильной матеше? или нужно будет еще ждать? и в таком случае, сколько примерно шагов осталось до полной подготовки?
Здравствуйте. Пожалуйста, продолжайте. Курс очень хороший, понятный и доступный. Вы проделали колоссальную работу
Так называемый обильный респект трудящимся над проектом. Вы удовлетворили мой вопрос “с чего начать влияние в математику с нуля” на по меньшей мере два месяца, вплоть до этого момента. И главное, теперь есть идеи по поводу дальнейшего изучения. Спасибо за это вот всё
Здравствуйте, не подскажите, в каком из уроков рассказывается про функции?
Это фантастически,Всю жизнь относила себа к гуманитариам ,а тут- каждый день занатий,как будто беседа с очень интересным человеком,А полюбила преобразованиа и уравнениа,Как будто детектив раскручиваешь,что же там в конце останетса,Спасибо огромное за труд и преподавательский талант,(простите в клавиатуре буквы западают)
Потому что гуманитариев не существует. И не только их, а и технарей, и естественников. Каждый способен к любой науке: просто нужно выкинуть из головы искусственно навязанные тебе другими (а часто самим же собой) ограничения.
Спасибо большое за этот самоучитель. Сегодня закончил последний на данный момент урок (75).
Здравствуйте, скажите, эта тема в каком классе изучается?
в 8-ом
спасибо большое за ваши уроки вы просто лучшие во всем рунете!!!!! благодаря вам я наконец то освоил основы математики и теперь могу понимать более сложные темы, кстати, могли бы вы сделать урок о логике, это бы отлично вписалось в вашу книгу
“Шаги” реально сделаны для отсталых,учился по этому тесту,всё показалось реальным бредом,много ненужной инфы,без которой можно обойтись,советую просто пройтись по урокам в ютубе,найти там себе учителя по душе,и заниматься по немногу,без этой стрёмной модульной дичи,которой не обязательно пользоваться.
Ну вот зачем критиковать? Раз такой ппц умный не заходи и не читай тя никто не заставляет, чел трудится и найдутся те кому нравится то как подробно он это объясняет…
Иди выпей, не мешай другим.
Вероятно, ты не можешь написать даже простенькую программу, иначе бы не говорил про “модульную дичь, которой не обязательно пользоваться”. А если можешь, то это тем более глупо, так как для программиста вопрос “Нужны ли модули?” даже не стоит.
Да и зачем тогда учился, если это бред? Просто пройди мимо и не сори.
Марина, я думаю, что он уже выпил, поэтому пытается философствовать.
Админ когда будут ли продолжения? или Вы забросили дело?
Не забросили. Продолжение будет.
Спасибо, а когда?
Когда?
И когда будут функции?
когда? пожалуйста продолжайте курс
Надеюсь у вас все получиться , уже 8 месяцев новой темы нет..
да, пожалуйста
Мы все ещё надеемся на продолжение!
Здравствуйте, спасибо за уроки они мне очень помогли понять математику, но было бы чудестно если бы вы опубликовали все уроки для полного изучения математики. Спасибо огромное Вам!
Надеюсь, администраторы сайта зарабатывают нормально с помощью этого ресурса, ибо, по моему мнению, объём рекламы здесь слишком незначителен.
Здравствуйте. А сюда добавят такие уроки как показательная функция, логарифмы, тригонометрические выражения? И если да, то когда примерно?
Здравствуйте, можете сказать когда примерно будут новые уроки
Здравствуйте. Сайт просто находка. Спасибо Вам большое за ваш труд. Хотелось бы узнать, сколько планируется вообще уроков?
Большое спасибо за ваш труд. Вы меняете жизни людей. Ваша доброта вернется вам!
Вопрос: До какого класса тут знания? Как оценить уровень ученика. Какие темы не затронуты? Что планируется?
Добрый день. Прошу Вас связаться со мной
Здравствуйте)) А будут ли еще уроки??
Когда будут матрицы, логика и прочее
Здравствуйте, скажите пожалуйста, с книжки какого по счету класса школьной программы стоит начать читать математику, после того как я хорошо освоил материал с сайта вашего? мне очень сильно нужна математика, потому что я програмистом хочу быть, а без нее как я успел увидеть, развитие очень ограничено
Админ пол года назад как последний раз ответил, почему нет новых уроков?
Интересно, какого тебе сидеть по ту сторону сайта, Админ?
А вообще, я, как и многие, хотел бы знать честный ответ относительно сайта, будет ли что-то новое в ближайшее время?
Понимаю, что сайт и так заслуживает огромного уважения за сам факт добродетели, но стоит ли надеяться на обновление в ближайший год? С любовью и уважением от Донни Кварко.
Тогда же будут новые уроки? Хочется уже увидеть высшую математику
Админ так и и не появлялся?)
Благодарю администрацию данного ресурса за труд!
Этих 75 разделов достаточно для подготовки к егэ по математике или требуется изучить еще доп. какие-то? Если не трудно, укажите, пожалуйста, заголовки тем, которые можно поискать самостоятельно.
не для егэ этого не хватит, если вы прошли 75 уроков советую продолжить вторым томом алгебры от киселева. прекрасный автор но читать немного трудно. я сам не из СНГ так что точно не знаю, но если в егэ затрагивается вышмат типа анализа то стоит двигатся дальше. после 75 шагов но этом сайте и второго тома киселева вы вышмат сможете освоить
Новых уроков не будет?
Никто не знает проект еще работает?) очень увлекательно) Создателю ресурса огромнейшее спасибо)
Огромное спасибо создателю этого великолепного проекта! Желаю вам здоровья и благополучия в новом году! Надеюсь и очень жду продолжения
Желаю вам здоровья и благополучия в новом году! Надеюсь и очень жду продолжения
Здравствуйте! Спасибо огромное за ваш труд, сайт замечательный, вами проделана огромная работа, процветания, благополучия всей вашей команде!
Я классическая мамочка в декрете. Отупела во время него страшно. Но благодаря вам я наконец могу соображать ахаахах
А если серьезно, спасибо большое, очень не хватает продолжения шагов <3
Добрый день.
Хотелось бы узнать.
Ообучение математике на даннос сайте за какие классы?
Админ ни один год уже прошел, ожидать ли нам нововведений или это конец проекта? Жаль, что вот так все закончилось…
Кто автор? Великолепно. Это должно быть школьным учебником!