Как разложить на множители квадратный трёхчлен
Квадратный трёхчлен – это многочлен вида ax2 + bx + c.
В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:
ax2 + bx + c = 0
Левая часть этого уравнения является квадратным трёхчленом.
Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.
Полученные корни x1 и x2 следует подстáвить в следующее выражение, которое и станет разложением:
a(x − x1)(x − x2)
Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:
ax2 + bx + c = a(x − x1)(x − x2)
Где левая часть – исходный квадратный трёхчлен.
Пример 1. Разложить на множители следующий квадратный трёхчлен:
x2 − 8x + 12
Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:
x2 − 8x + 12 = 0
В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:
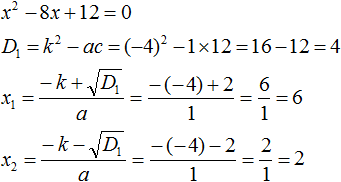
Итак, x1 = 6, x2 = 2. Теперь воспользуемся формулой:
ax2 + bx + c = a(x − x1)(x − x2)
В левой части вместо выражения ax2 + bx + c напишем свой квадратный трёхчлен x2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x1 = 6, x2 = 2
x2 − 8x + 12 = 1(x − 6)(x − 2) = (x − 6)(x − 2)
Если a равно единице (как в данном примере), то решение можно записать покороче:
x2 − 8x + 12 = (x − 6)(x − 2)
Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.
Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2). Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x2 − 8x + 12
(x − 6)(x − 2) = x2 − 6x − 2x + 12 = x2 − 8x + 12
Пример 2. Разложить на множители следующий квадратный трёхчлен:
2x2 − 14x + 24
Приравняем данный квадратный трёхчлен к нулю и решим уравнение:
2x2 − 14x + 24 = 0
Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:
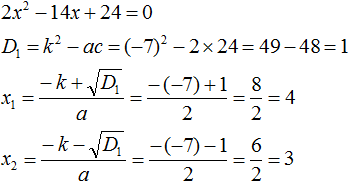
Итак, x1 = 4, x2 = 3. Приравняем квадратный трехчлен 2x2 − 14x + 24 к выражению a(x − x1)(x − x2), где вместо переменных a, x1 и x2 подстáвим соответствующие значения. В данном случае a = 2
2x2 − 14x + 24 = 2(x − 4)(x − 3)
Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x2 − 14x + 24
2(x − 4)(x − 3) = 2(x2 − 4x −3x + 12) = 2(x2 − 7x + 12) = 2x2 − 14x + 24
Как это работает
Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.
Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:
x2 + bx + c
Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:

Тогда приведённый квадратный трехчлен x2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x1 + x2 = −b. Для этого можно умножить обе его части на −1
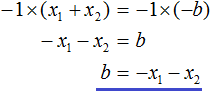
Переменную c из теоремы Виета выражать не нужно – она уже выражена. Достаточно поменять местами левую и правую часть:
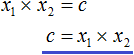
Теперь подставим выраженные переменные b и c в квадратный трёхчлен x2 + bx + c
![]()
Раскроем скобки там где это можно:
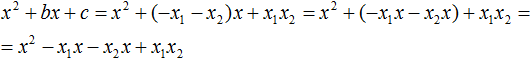
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
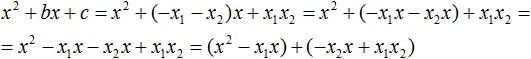
Из первых скобок вынесем общий множитель x, из вторых скобок – общий множитель −x2
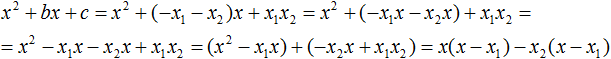
Далее замечаем, что выражение (x − x1) является общим множителем. Вынесем его за скобки:
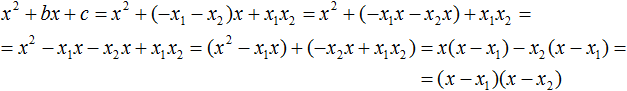
Мы пришли к тому, что выражение x2 + bx + c стало равно (x − x1)(x − x2)
x2 + bx + c = (x − x1)(x − x2)
Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.
Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a
ax2 + bx + c = a(x − x1)(x − x2)
Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax2 + bx + c = 0, то теорема Виета принимает следующий вид:

Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a

Далее чтобы квадратный трёхчлен вида ax2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 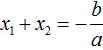 и
и ![]()
Для начала выразим b и c. В первом равенстве умножим обе части на a. Затем обе части получившегося равенства умножим на −1
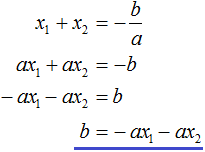
Теперь из второго равенства выразим c. Для этого умножим обе его части на a
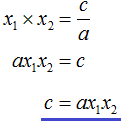
Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax2 + bx + c. Для наглядности каждое преобразование будем выполнять на новой строчке:
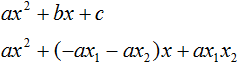
Здесь вместо переменных b и c были подставлены выражения −ax1 − ax2 и ax1x2, которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:
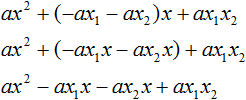
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
![]()
Теперь из первых скобок вынесем общий множитель ax, а из вторых – общий множитель −ax2
![]()
Далее замечаем, что выражение x − x1 тоже является общим множителем. Вынесем его за скобки:
![]()
Вторые скобки содержат общий множитель a. Вынесем его за скобки. Его можно расположить в самом начале выражения:
![]()
Мы пришли к тому, что выражение ax2 + bx + c стало равно a(x − x1)(x − x2)
ax2 + bx + c = a(x − x1)(x − x2)
Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x1)(x − x2) вместо переменных x1 и x2.
Примеры разложений
Пример 1. Разложить на множители следующий квадратный трёхчлен:
3x2 − 2x − 1
Найдём корни квадратного трёхчлена:
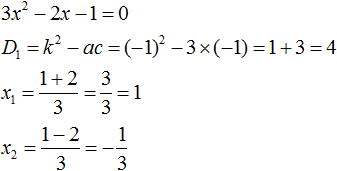
Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x2 − 2x − 1, а в правой части – его разложение в виде a(x − x1)(x − x2), где вместо a, x1 и x2 подстáвим соответствующие значения:
![]()
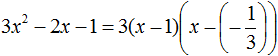
Во вторых скобках можно заменить вычитание сложением:
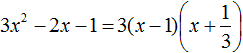
Пример 2. Разложить на множители следующий квадратный трёхчлен:
3 − 11x + 6x2
Упорядочим члены так, чтобы старший коэффициент располагался первым, средний – вторым, свободный член – третьим:
6x2 − 11x + 3
Найдём корни квадратного трёхчлена:
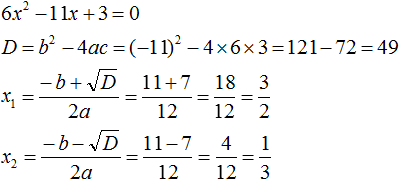
Воспользуемся формулой разложения:
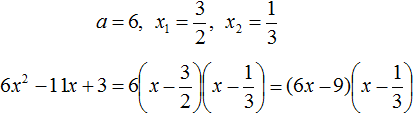
Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3
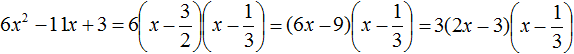
Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:
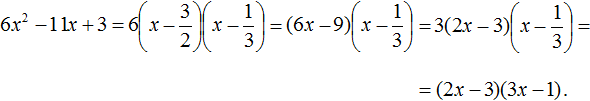
Пример 3. Разложить на множители следующий квадратный трёхчлен:
3x2 + 7x − 6
Найдём корни квадратного трёхчлена:
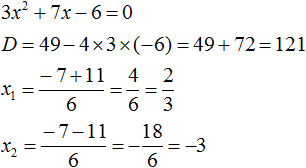
Воспользуемся формулой разложения:
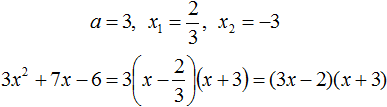
Пример 4. Найдите значение k, при котором разложение на множители трёхчлена 3x2 − 8x + k содержит множитель (x − 2)
Если разложение содержит множитель (x − 2), то один из корней квадратного трёхчлена равен 2. Пусть корень 2 это значение переменной x1
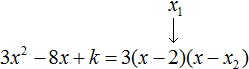
Чтобы найти значение k, нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.
В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби ![]() , а произведение корней – дроби
, а произведение корней – дроби ![]()
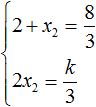
Выразим из первого равенства переменную x2 и сразу подстáвим найденное значение во второе равенство вместо x2
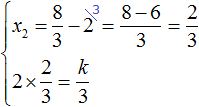
Теперь из второго равенства выразим k. Так мы найдём его значение.
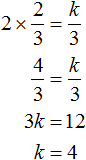
Пример 5. Разложить на множители следующий квадратный трёхчлен:
![]()
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим ![]() . Если поменять местами сомножители, то получится
. Если поменять местами сомножители, то получится ![]() . То есть коэффициент a станет равным
. То есть коэффициент a станет равным ![]()
Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:
![]()
Найдём корни квадратного трёхчлена:
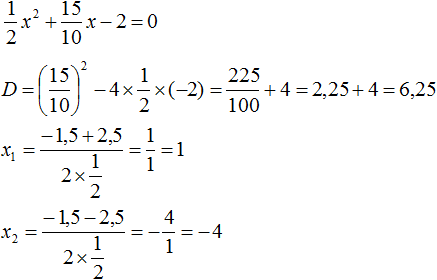
Воспользуемся формулой разложения:
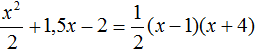
Когда корень только один
Если квадратный трёхчлен имеет только один корень, то формула разложения квадратного трёхчлена примет такой вид:
ax2 + bx + c = a(x − x1)2
Вместо x1 подставляется единственный найденный корень квадратного трёхчлена.
Например, квадратный трёхчлен x2 − 6x + 9 имеет только один корень. Дискриминант этого квадратного трёхчлена равен нулю:
D = b2 − 4ac = (−6)2 − 4 × 1 × 9 = 36 − 36 = 0
и далее вычисляется единственный корень по известной формуле:
![]()
Тогда по формуле, которая приведена выше, получим:
ax2 + bx + c = a(x − x1)2
x2 − 6x + 9 = (x − 3)2
Внимательные наверное сразу поняли почему происходит именно так. Если дискриминант квадратного трёхчлена равен нулю, то корень вычисляется по формуле:
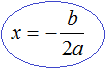
Но никто не запрещает нам использовать формулы вычисления корней квадратного трёхчлена:


Просто в этом случае мы получим один и тот же корень 3
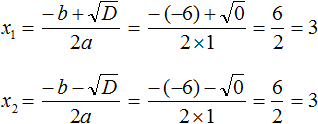
Видим, что x1 = x2. Теперь для квадратного трёхчлена x2 − 6x + 9 применим нашу формулу разложения, которую мы применяем когда два корня:
x2 − 6x + 9 = (x − 3)(x − 3)
Выражение (x − 3)(x − 3) это перемножение двух сомножителей, каждый из которых равен (x − 3). Это выражение можно заменить на выражение (x − 3)2
x2 − 6x + 9 = (x − 3)2
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
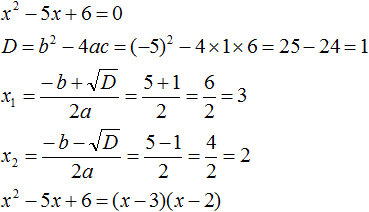
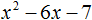

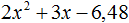
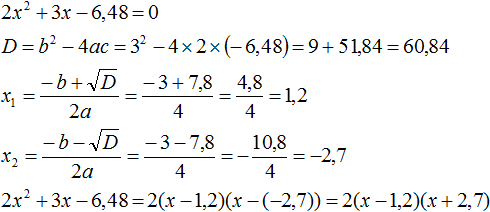
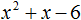
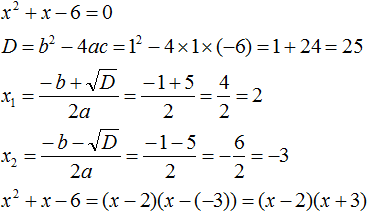
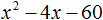
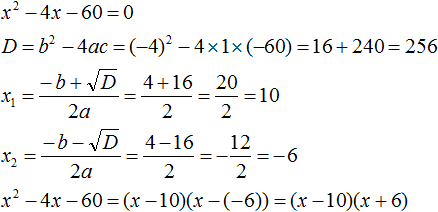
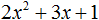
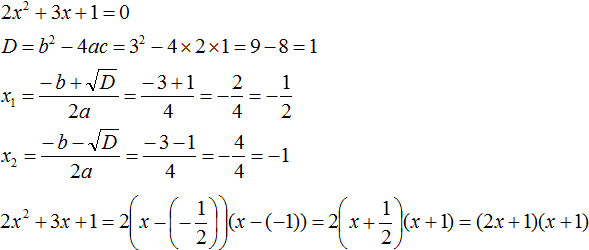
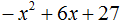
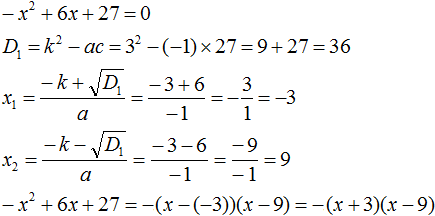
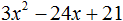
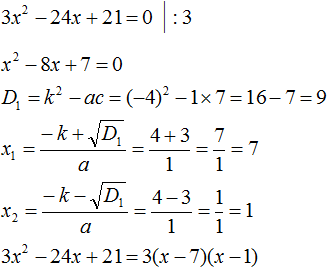
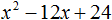
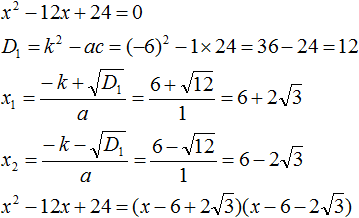
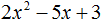
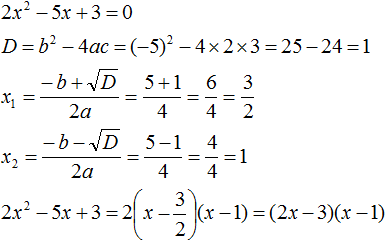
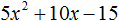
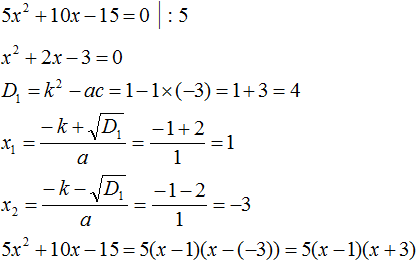
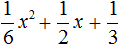
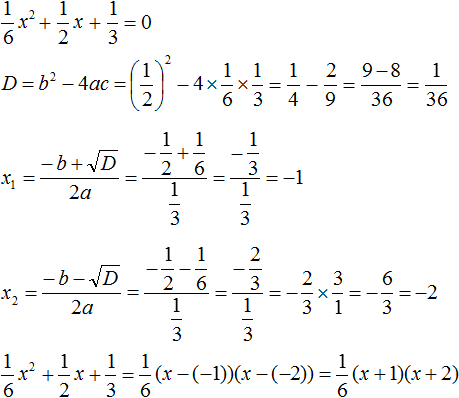
Еще уроки будут?
Конечно
Вам от меня небольшой денежный подарок. Всё что мог. Спасибо за всё
Большое спасибо, не сто́ило)
Скажите пожалуйста, хотя бы примерный сроки, когда можно ожидать новые уроки.
Страшно испугался, когда увидел, что ваш сайт заблокирован(или не активирован).
Спасибо за Ваш бесценный, и воистинну альтруистический труд; Надеюсь поблагодарить вас когда-нибудь не только словами. Всего вам найлучшего.
Здравствуйте! Подскажите, пожалуйста, можно ли за 1,5 месяца освоить всю математику для поступления в ВУЗ? Сейчас дошла до буквенных чисел, хочу знать есть ли у меня реальные шансы, если заниматься ежедневно?
конечно нет, я занимаясь почти каждый день на этом сайте потратила около полугода, вот сегодня прохожу последний урок
С чего это нет? За 2 месяца вполне можно пройти все уроки, если уделять по 4 часа в день.
Если не просто листать, а работать с черновиками и писать в чистовик, перерешивать самим разбираемые примеры при подаче материала, то..последние 19 глав у меня заняли 60 часов. Это при условии, что школу закончил 20 лет назад, математика была хорошо, но не отлично. Так что считайте сами, исходя из базовых компетенций.
здраствуйте к котором класу ета програма и когда курси ищо
Кажется нет
Спасибо Вам за работу! Будет ли продолжение материала?!
Админ Спасибо Вам! Не скажете приблизительно сколько уроков будет?
Огромнейшее спасибо за информацию и материалы! Высылаю вам свои глубочайшие и ярчайшие ноты благодарности!
Ученик 9-го класса Одесской ООШ №73
Григорян Гарик.
Спасибо и Вам! Желаем успехов в науке.
Спасибо за Ваш труд. Все так доходчиво и ясно.
Привет админ, до какого класса идет данный курс?
На сайте смешанная программа, не привязанная к классам. В одном уроке могут затрагиваться темы как из младших, так и и старших классов.
Видно, что вас учили сейчас -нужно, выделить полный квадрат и далее по списку-в местных учебниках-академический курс -пытался понять как там решено иррациональное уравнение-потом решил как меня учили учителя у которых был орден Ленина и получил-4=16-храню ксерокс-кафедра теорфизики, а мехмат плакал от восторга-видно где вас учили….
А может тогда вам нас поучить, как это делать, создайте сайт, серию уроков, тогда посмотрим чей метод более доходчив, а то критиковать может каждый, а реально полезные дела, как автор сайта, почти никто не делает.
“…и далее по списку” – похоже это все чем можете оперировать вы…. Человек напрягся, дело сделал, и сделал хорошо. А вы только ржать умеете всем мехматом…. Нос задирать не надо. Не нравится – сделай лучше. Меня так в школе учили… Но Вы, похоже, в других школах обучались…
Когда будет следующий урок?
Спасибо большущее!!!
Только с помощью вашего сайта к сорока годам я понял, что математика может быть интересна. Материал раскрыт грамотно, доступно, доходчиво, понятно, с повторами. Сайт полезен как для молодого поколения так и взрослых. А в связи с последними изменениями в пенсионной системе, влияющие на увеличение доли работающего населения в переквалификации и перепрофориентации, данный материал просто необходим, но в вашем изложении он просто бесценен. Большое спасибо Вашей команде специалистов. Единственная просьба- продолжать выдавать уроки с дальнейшим углублением. Ваш сайт как увлекательный роман, надеюсь с продолжением. Спасибо!!!
Спасибо и Вам! Будем стараться)
Здравствуйте,а эти 63 урока будут достаточны для сдачи Егэ?
спасибо огромное соиздателю сайта, тебе это зачтётся, старичок, продолжай в том же духе
зашла посмотреть, а что там в конце…..шаг 69…..мне кажется я этого никогда не пойму, хотя в школе до 6 класса училась на отлично, математику очень любила.
С помощью этого сайта я начинаю видеть красоту в цифрах, это невероятно
Админ, когда продолжение?
Добрый вечер! Влюблена в Ваш сайт, каждый день занимаюсь, пишу узнать когда будут новые уроки? В любом случае с нетерпением жду. Заранее благодарю за ответ и огромное спасибо за то, что Вы делаете! <3
Здравствуйте.
Спасибо и Вам)
Когда точно будут новые уроки неизвестно. Но скоро)
Я тоже реально влюбилась в математику, раньше в школе противна была, сейчас готовлюсь к поступлению, нашла этот замечательный сайт, и за полгода освоила то,чего не освоила за школьные годы!Спасибо админам!
Сколько еще осталось тем до окончания школьной программы с алгебры и геометрии??
Очень много
Добрый день, влюбился в ваш сайт, всё очень удобно и по полочкам, минимализм и простота, обучаться по этому сайту один кайф. Поставил цель за 30 дней научиться всем 69 шагам. Сейчас уже подхожу к концу. Надеюсь уроков будет ещё больше)
Здравствуйте, Админ, спасибо огромное за этот сайт! Я очень благодарен вам, в математике я был плох, в августе прошлого года наткнулся на ваш сайт, и начал изучать с нуля, за полгода освоил всю базу, без этого сайта я бы не достиг таких результатов в математике, ещё раз благодарю за этот сайт!
Здравствуйте, а темы по корням будут?
Добрый вечер. Ребята, спасибо вам за ваш сайт. Пожалуйста, подскажите когда приблизительно появятся новые уроки?Умоляю, успокойте!)
Здравствуйте. Сами не знаем. Надеемся что скоро…
Здравствуйте, спасибо вам огромное за этот сайт и доступ к очаровательной математике. Не понимаю, как я могла не любить её?:) ещё на 18 уроке, но волнуюсь, вы же не прекратите свою деятельность?
Правда, я нашла сокровище…
очень ждем
Да, действительно ждём!
Очень большое спасибо вам. Я изучаю ваши уроки прямо с Узбекистана. Реально уникальный сайт. Но возникает вопрос : Как скоро начнутся ваши следующие уроки, ну хоть примерно?
прям с Ташкента? Я тоже оттуда изучаю)
Привет из Таджикистана))
Спасибо вам!Смогу ли я сдать вступительные экзамены благодаря изученному материалу?
Добрый день).
Какую тему нужно изучать после этого?
Здравствуйте, начинаю изучение математики, решил заглянуть в самый низ 🙂 Хотелось бы узнать, много тем осталось до конца школьной программы? И где можете посоветовать продолжить обучение после этого учебника?
Прошел все 69 тем, не спеша, за 2.5 недели. Вопросов не возникало. Доступно и доходчиво доносится информация до потребителя!
Здравствуйте, учу программирование и столкнулся с тем что нужно параллельно учить математику, буквально с нуля, прохожу у вас на сайте, большое человеческое спасибо за проделанную работу, могли бы вы
посоветовать какие либо учебники для обучения после данного курса?, буду очен признателен.
Сколько еще тем осталось к интегралам??(Пж очень нужно знать)
Привет, если нужна помощь при составлении уроков или ещё какая либо помощь, буду рад помочь
Очень прошу, продолжайте! Это единственный ресурс с которым у меня с удовольствием получается учить математику…очень жду следующих уроков.
Дорогие админы, хочу выразить огромную благодарность за создание такого сайта. Изучала математику с Вами в течение полугода, сегодня крайний урок. Прошу не бросайте Ваше дело, очень нужны темы :Интегралы, логарифмы , логика, темы по тригонометрии, стереометрии. Заранее благодарю.
Спасибо, будем стараться)
Желаем Вам успехов в дальнейшем обучении.
Всех этих хватает на все 11 классов, или меньше?
на 8-9
Когда новые уроки? Скажите пожалуйста
Вы случайно не забросили проект?
Вы забросили курсы?
Нет
Спасибо за проделанную работу! Вот жаль только, что до логарифмов еще ой как не скоро) как с 8 по 11 класс)
Огромное вам спасибо! Какой темой будет следующий урок?
Вы даже и не представляйте какое благое дело делайте. В жизни не видел лучшего объяснения так мною ненавистной математики(с вашей помощью уже любимой математики)
Чувствуется мне готовится большой материал с продолжением и нас ждут чудеса математики!
здраствуйте к котором класу ета програма и когда курси ищо
Когда будут новые уроки?
Только что завершил этот курс математики и крайне благодарен, жду новых материалов.
С “нулевых” знаний дошел до этой главы за 4 месяца (сентябрь-декабрь). Занимаясь весьма много и прорешивая все примеры\ДЗ.
Крайне хорошее введение в математику, над многими темами пришлось попотеть, но удовольствие от понимания таких вещей перевешивает затраченное время.
Всех учащихся с наступающим 2021 годом, желаю в следующем году выжить
Надеюсь создатель сайта бодро перенес пандемию. Здоровья!
Здравствуйте! Очень ждем продолжения.
Что случилось с сайтом? уже год нету новых уроков
в процессе…
Добрый времени суток! Скажите, пожалуйста, в каких классах начинают проходить то, что изложено в последнем уроке? Какого уровня материал изложен на этом сайте на данный момент?
Большое Спасибо!
Не ну, команда создателей красавчики, огромное вам спасибо, что создали данный сайт.