Если неравенство содержит два и более модуля, его удобнее решать методом интервалов.
Процесс решения неравенств с модулем методом интервалов во многом похож на процесс решения уравнений с модулем методом интервалов.
Рассмотрим несколько примеров.
Пример 1. Решить неравенство |7 − x|+|2x + 3|< 16
Решение
Для начала находим такие x, при которых подмодульные выражения 7 − x и 2x + 3 обращаются в ноль. Для этого приравняем эти выражения к нулю и решим простейшие линейные уравнения:
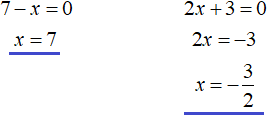
Отметим числа 7 и ![]() на координатной прямой. Мéньшие числа отмечаем левее, бóльшие правее:
на координатной прямой. Мéньшие числа отмечаем левее, бóльшие правее:

Получили три промежутка: ![]() ,
, ![]() и
и ![]() Теперь необходимо решить исходное неравенство на каждом из этих промежутков. Надо иметь ввиду, что на каждом из этих промежутков модули исходного неравенства могут раскрываться по-разному.
Теперь необходимо решить исходное неравенство на каждом из этих промежутков. Надо иметь ввиду, что на каждом из этих промежутков модули исходного неравенства могут раскрываться по-разному.
Решим исходное неравенство на первом промежутке ![]()
Далее рассуждаем так:
Если ![]() , то при любом значении x на данном промежутке подмодульное выражение 7 − x станет неотрицательным, а значит модуль |7 − x| на промежутке
, то при любом значении x на данном промежутке подмодульное выражение 7 − x станет неотрицательным, а значит модуль |7 − x| на промежутке ![]() будет раскрываться со знаком плюс. Второй модуль |2x + 3| на промежутке
будет раскрываться со знаком плюс. Второй модуль |2x + 3| на промежутке ![]() будет раскрываться со знаком минус.
будет раскрываться со знаком минус.
Тогда в результате раскрытия модулей на промежутке ![]() исходное неравенство примет вид:
исходное неравенство примет вид:
![]()
Решим данное неравенство:
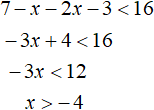
Итак, сейчас мы рассматриваем промежуток ![]() . И решив на этом промежутке исходное неравенство мы получили неравенство x > −4.
. И решив на этом промежутке исходное неравенство мы получили неравенство x > −4.
Теперь начинается самое интересное. Надо выяснить выполняется ли неравенство x > −4 на промежутке ![]() . Или задать такой вопрос: «при каких значениях промежутка
. Или задать такой вопрос: «при каких значениях промежутка ![]() выполняется неравенство x > −4»
выполняется неравенство x > −4»
Для наглядности нарисуем еще одну координатную прямую и изобразим на ней решения неравенства x > −4 и ![]()

На рисунке видно при каких значениях промежутка ![]() выполняется неравенство x > −4. Эти значения лежат в промежутке от −4 до
выполняется неравенство x > −4. Эти значения лежат в промежутке от −4 до ![]()
Значит первым нашим решением будет промежуток от −4 до ![]()
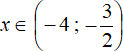
Решим теперь исходное неравенство на промежутке ![]()
Если ![]() , то при любом значении x на данном промежутке подмодульное выражение 7 − x станет неотрицательным, а значит модуль |7 − x| на промежутке
, то при любом значении x на данном промежутке подмодульное выражение 7 − x станет неотрицательным, а значит модуль |7 − x| на промежутке ![]() будет раскрываться со знаком плюс. Второй модуль |2x + 3| на промежутке
будет раскрываться со знаком плюс. Второй модуль |2x + 3| на промежутке ![]() тоже будет раскрываться со знаком плюс.
тоже будет раскрываться со знаком плюс.
После раскрытия модулей на промежутке ![]() исходное неравенство примет вид:
исходное неравенство примет вид:
![]()
Решим данное неравенство:
![]()
Cейчас мы рассматриваем промежуток ![]() . И решив на этом промежутке исходное неравенство мы получили неравенство x < 6. Теперь надо выяснить выполняется ли неравенство x < 6 при
. И решив на этом промежутке исходное неравенство мы получили неравенство x < 6. Теперь надо выяснить выполняется ли неравенство x < 6 при ![]()
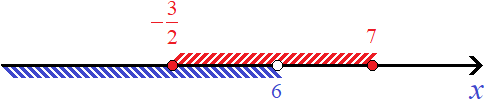
Неравенство x < 6 выполняется не на всём промежутке ![]() , а лишь на промежутке
, а лишь на промежутке ![]() до 6. Запишем наше второе решение:
до 6. Запишем наше второе решение:
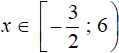
Решим теперь исходное неравенство на последнем промежутке ![]()
Если ![]() , то при любом значении x на данном промежутке подмодульное выражение 7 − x станет отрицательным, а значит модуль |7 − x| на промежутке
, то при любом значении x на данном промежутке подмодульное выражение 7 − x станет отрицательным, а значит модуль |7 − x| на промежутке ![]() будет раскрываться со знаком минус. Второй модуль |2x + 3| на промежутке
будет раскрываться со знаком минус. Второй модуль |2x + 3| на промежутке ![]() будет раскрываться со знаком плюс.
будет раскрываться со знаком плюс.
Тогда в результате раскрытия модулей на промежутке ![]() исходное неравенство примет вид:
исходное неравенство примет вид:
![]()
Решим данное неравенство:
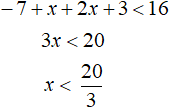
Cейчас мы рассматриваем промежуток ![]() . И решив на этом промежутке исходное неравенство мы получили неравенство
. И решив на этом промежутке исходное неравенство мы получили неравенство ![]() , Теперь надо выяснить выполняется ли неравенство
, Теперь надо выяснить выполняется ли неравенство ![]() при
при ![]()

Мы видим, что неравенство ![]() не выполняется ни при каких значениях промежутка
не выполняется ни при каких значениях промежутка ![]() . Это значит, что исходное неравенство на промежутке
. Это значит, что исходное неравенство на промежутке ![]() решений не имеет.
решений не имеет.
Действительно, возьмём любое число из промежутка ![]() , например, число 9 и подставим его в исходное неравенство. В результате получим неравенство которое не выполняется:
, например, число 9 и подставим его в исходное неравенство. В результате получим неравенство которое не выполняется:
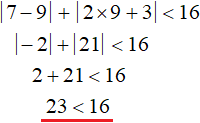
Теперь нужно собрать воедино ответы, которые мы получили на каждом промежутке. Чтобы сделать это, просто объединим промежутки 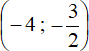 и
и 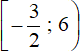
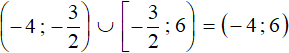
Ответ: (−4 ; 6).
Пример 2. Решить неравенство: 3|x − 2|+|5x − 4| ≤ 10
Решение
Найдём x, при которых подмодульные выражения x − 2 и 5x − 4 обращаются в ноль. Для этого приравняем эти выражения к нулю и решим простейшие линейные уравнения:
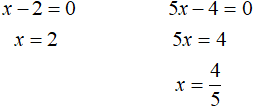
Отметим числа 2 и ![]() на координатной прямой:
на координатной прямой:
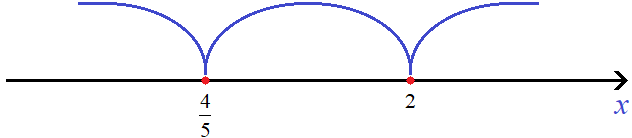
Решим исходное неравенство на промежутке ![]() . Оба модуля на данном промежутке раскрываются с минусом:
. Оба модуля на данном промежутке раскрываются с минусом:
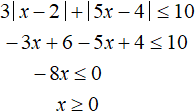
Полученное неравенство x ≥ 0 выполняется не на всем промежутке ![]() , а только на промежутке от 0 до
, а только на промежутке от 0 до ![]()
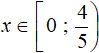
Решим теперь исходное неравенство на следующем промежутке ![]() . На данном промежутке модуль|x − 2| раскрываются с минусом, а модуль |5x − 4| с плюсом:
. На данном промежутке модуль|x − 2| раскрываются с минусом, а модуль |5x − 4| с плюсом:
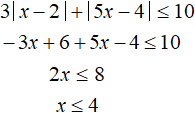
Полученное неравенство x ≤ 4 выполняется на всём промежутке ![]() . Значит на промежутке
. Значит на промежутке ![]() исходное неравенство имеет следующее решение:
исходное неравенство имеет следующее решение:
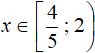
Решим исходное неравенство на следующем промежутке x ≥ 2. Оба модуля на данном промежутке раскрываются с плюсом:
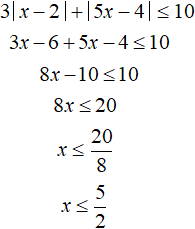
Полученное неравенство ![]() выполняется не на всем промежутке x ≥ 2, а только на промежутке от 2 до
выполняется не на всем промежутке x ≥ 2, а только на промежутке от 2 до ![]()
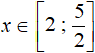
Запишем окончательный ответ. Для этого объединим промежутки 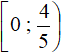 ,
, 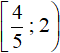 и
и 
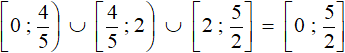
Ответ: 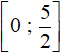 .
.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
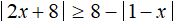
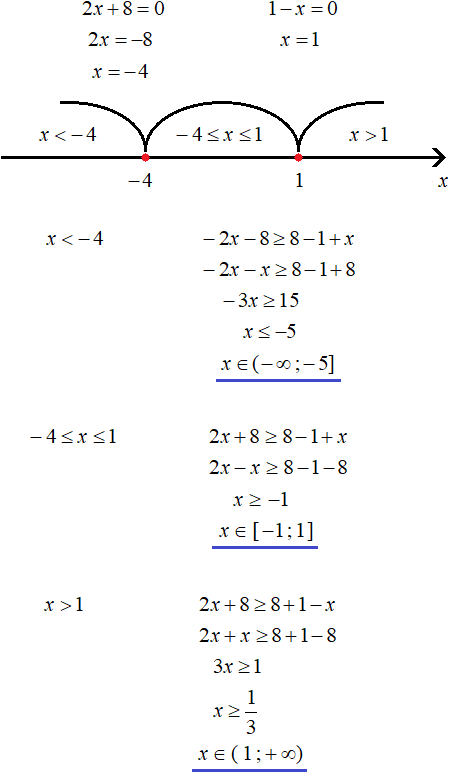
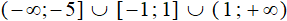 .
.
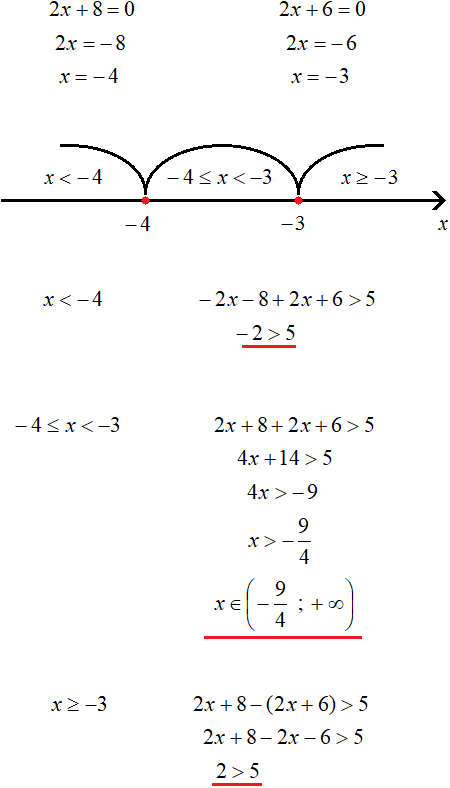

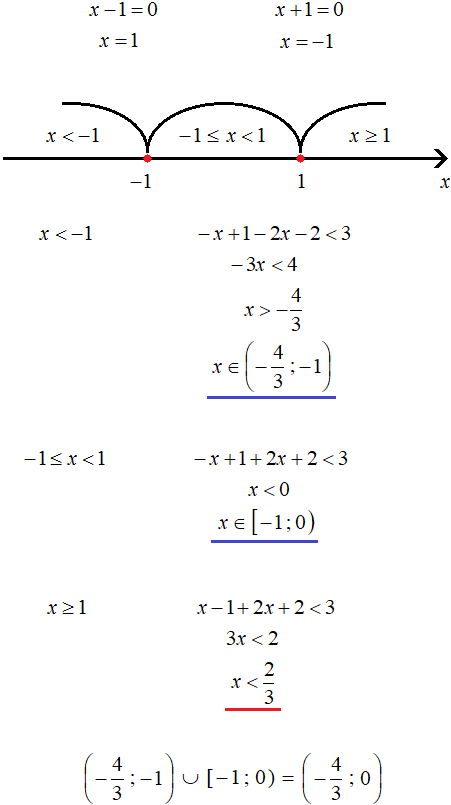
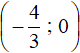 .
.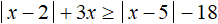
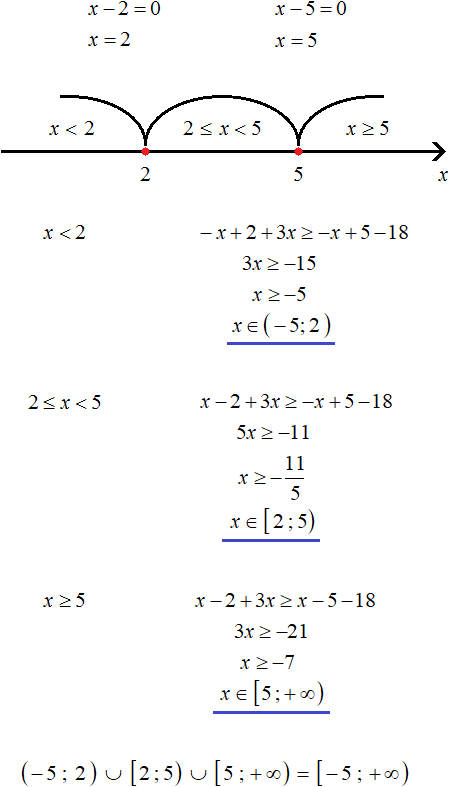
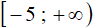 .
.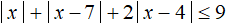
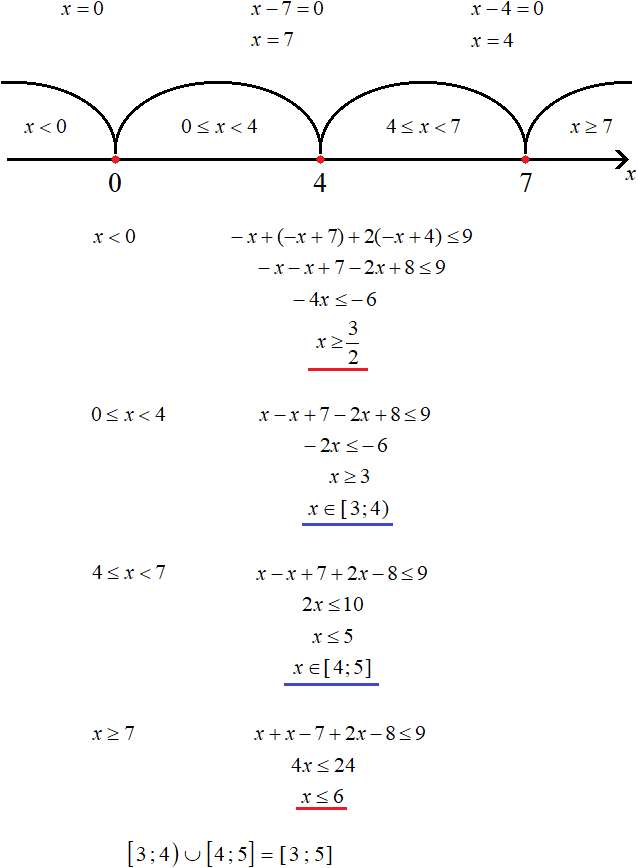
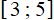 .
.
Класс, спасибо!
Уважаемый создатель сайта огромная тебе благодарность, создав прекрасный сайт ты помог мне войти в мир чисел и узнать красоту математики, желаю тебе всех благ, процветания в жизни, огромных успехов, надеюсь проект не забросишь, благое дело)
большое спасибо всем кто работает над этим сайтом, занимаюсь с вами больше полу года. вы очень помогаете детям у которых не всегда могут быть возможности на репетитора и т.п. процветания вам!
Красавчик
Большое спасибо всем, кто создавал сайт и весь материал. Помогли многим, спасибо
Здравствуйте! В 1 задании при x > 1, x точно принадлежит (2; +∞), а не (1; +∞)?
да, там опечатка