В данном уроке мы рассмотрим понятие модуля числа более подробно.
Что такое модуль?
Модуль – это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3
| 3 |= 3
|−3|= 3
Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:
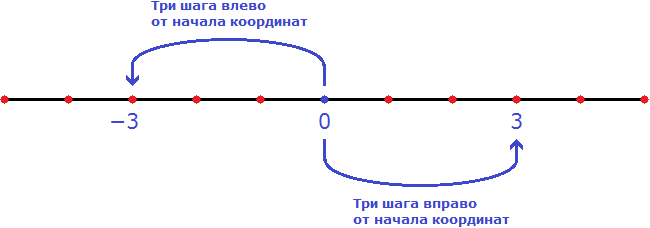
Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:
|x1 − x2|
Где x1 и x2 – числа на координатной прямой.
Например, отметим на координатной прямой числа 2 и 5.
![]()
Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:
|2 − 5| = |−3| = 3
Видим, что расстояние от числа 2 до числа 5 равно трём шагам:

Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3

То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:
|5 − 2| = | 3 | = 3
Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:
|x1 − x2| = |x2 − x1|
Это равенство можно прочитать так: Расстояние от x1 до x2 равно расстоянию от x2 до x1.
Раскрытие модуля
Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.
Правило раскрытия модуля выглядит так:
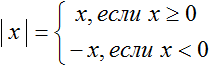
Такую запись мы ранее не использовали. Дело в том, что равенство можно задавать несколькими формулами. Фигурная скобка указывает, что возможны два случая в зависимости от условия. В данном случае условиями являются записи «если x ≥ 0» и «если x < 0».
В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.
Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x < 0, то под знáком модуля располагается отрицательное число. После знака равенства нужно подстáвить данное отрицательное число вместо x и раскрыть скобки.
Например, найдём модуль числа −7, используя правило раскрытия модуля:
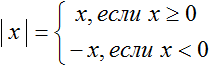
Итак, x = −7
|−7|
В данном случае выполняется второе условие x < 0, ведь −7 < 0
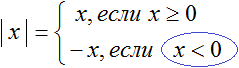
Поэтому используем вторую формулу. А именно |x| = −x. Подстáвим вместо x число −7
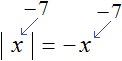
Отсюда:
![]()
Поэтому |−7| = 7.
Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5
| 5 |
В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0
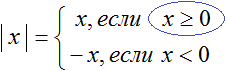
Поэтому используем первую формулу. А именно | x | = x. Получаем | 5 | = 5.
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:
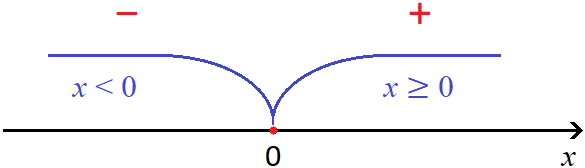
На рисунке красные знаки минуса и плюса указывают как будет раскрываться модуль |x| на промежутках x < 0 и x ≥ 0.
К примеру, если взять числа 1, 9 и 13, а они принадлежат промежутку x ≥ 0, то согласно рисунку модуль |x| раскроется со знаком плюс:
| 1 | = 1
| 9 | = 9
| 13 | = 13
А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:
|−3| = −(−3) = 3
|−9| = −(−9) = 9
|−15| = −(−15) = 15
Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,
|√4 − 6|
Корень из числа 4 равен 2. Тогда модуль примет вид
|√4 − 6| = |2 − 6| = |−4|
x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x < 0, ведь −4 < 0
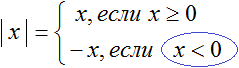
Следовательно, используем вторую формулу |x| = −x. Продолжаем решение в исходном примере:
|√4 − 6| = |2 − 6| = |−4| = −(−4) = 4
На практике обычно рассуждают так:
“Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля”.
Примеры:
|2| = 2 – модуль раскрылся со знаком плюс, поскольку 2 ≥ 0
|−4| = −(−4) = 4 – модуль раскрылся со знаком минус, поскольку −4 < 0
В некоторых учебниках можно встретить следующую запись правила раскрытия модуля:
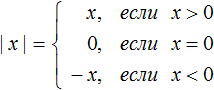
В этой записи первое условие которое ранее выглядело как x ≥ 0 расписано подробнее, а именно сказано что если x > 0, то выражение |x| будет равно x, а если x=0, то выражение |x| будет равно нулю.
Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:
| 0 |
В данном случае выполняется условие x=0, ведь 0 = 0
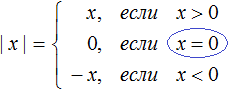
Отсюда: |0| = 0
Пример 5. Раскрыть модуль в выражении |x|+ 3
Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.
Если x < 0, то модуль раскроется со знаком минус, и тогда исходное выражение примет вид −x + 3. Чтобы сделать это выражение более удобным для восприятия, поменяем местами его члены, полýчим 3 − x
Теперь запишем решение так:
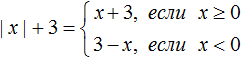
Проверим это решение при произвольных значениях x.
Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:
|x|+ 3 = x + 3 = 5 + 3 = 8
Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 < 0, то модуль содержащийся в выражении |x|+ 3 раскроется со знаком минус и тогда решение примет вид:
|x| + 3 = 3 − x = 3 − (−6) = 9
Пример 6. Раскрыть модуль в выражении x +|x + 3|
Если x + 3 ≥ 0, то модуль |x + 3| раскроется со знаком плюс и тогда исходное выражение примет вид x + x + 3, откуда 2x + 3.
Если x + 3 < 0, то модуль |x + 3| раскроется со знаком минус и тогда исходное выражение примет вид x − (x + 3), откуда x − x − 3 = −3.
Запишем решение так:
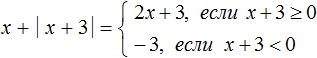
Заметим, что условия x + 3 ≥ 0 и x + 3 < 0 являются неравенствами. Их можно привести к более простому виду, решив их:
![]()
Тогда условия из решения можно заменить на равносильные x ≥ −3 и x < −3
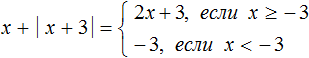
Во втором случае когда x строго меньше −3 выражение x +|x + 3| всегда будет равно постоянному числу −3.
Например, найдём значение выражения x +|x + 3| при x = −5. Поскольку −5 < −3, то согласно нашему решению значение выражения x +|x + 3| будет равно −3
При x = −5,
x +|x + 3| = x − x − 3 = −5 − (−5) − 3 = −3
Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11
При x = 4,
x +|x + 3| = 2x+3 = 2 × 4 + 3 = 8 + 3 = 11
Найдём значение выражения x +|x + 3| при x=−3.
Поскольку −3 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив −3 получим −3
x +|x + 3| = 2x + 3 = 2 × (−3) + 3 = −6 + 3 = −3
Пример 3. Раскрыть модуль в выражении ![]()
Как и прежде используем правило раскрытия модуля:
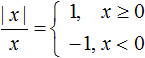
Но это решение не будет правильным, поскольку в первом случае написано условие x ≥ 0, которое допускает что при x = 0 знаменатель выражения ![]() обращается в ноль, а на ноль делить нельзя.
обращается в ноль, а на ноль делить нельзя.
В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0
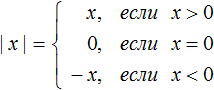
Перепишем решение так:
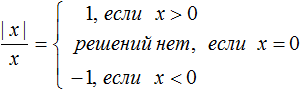
В первом случае написано условие x > 0. Тогда выражение ![]() станет равно 1. Например, если x = 3, то числитель и знаменатель станут равны 3, откуда полýчится 1
станет равно 1. Например, если x = 3, то числитель и знаменатель станут равны 3, откуда полýчится 1
![]()
И так будет при любом x, бóльшем нуля.
Во втором случае написано условие x = 0. Тогда решений не будет, потому что на ноль делить нельзя.
В третьем случае написано условие x < 0. Тогда выражение ![]() станет равно −1. Например, если x = −4, то числитель станет равен 4, а знаменатель −4, откуда полýчится единица −1
станет равно −1. Например, если x = −4, то числитель станет равен 4, а знаменатель −4, откуда полýчится единица −1
![]()
Пример 4. Раскрыть модуль в выражении ![]()
Если x ≥ 0, то модуль, содержащийся в числителе, раскроется со знаком плюс, и тогда исходное выражение примет вид ![]() , которое при любом x, бóльшем нуля, будет равно единице:
, которое при любом x, бóльшем нуля, будет равно единице:
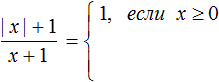
Если x < 0, то модуль раскроется со знаком минус, и тогда исходное выражение примет вид ![]()
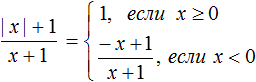
Но надо учитывать, что при x = − 1 знаменатель выражения ![]() обращается в ноль. Поэтому второе условие x < 0 следует дополнить записью о том, какие значения может принимать x
обращается в ноль. Поэтому второе условие x < 0 следует дополнить записью о том, какие значения может принимать x
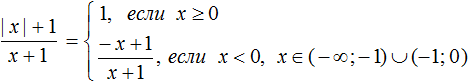
Преобразование выражений с модулями
Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.
Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.
Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.
Решение
Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:
![]()
Раскроем модуль в получившемся выражении. Если x ≥ 0, то получим 3x − 2x + 5y, откуда x + 5y.
Если x < 0, то получим −3x − 2x + 5y, откуда −5x + 5y. Вынесем за скобки множитель −5, получим −5(x − y)
В итоге имеем следующее решение:
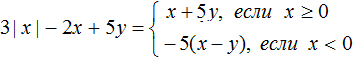
Пример 2. Раскрыть модуль в выражении: −|x|
Решение
В данном случае перед знаком модуля стоит минус. Его можно понимать как минус единицу перед знаком модуля. Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид −x
Если x < 0, то модуль раскроется со знаком минус, и тогда исходное выражение примет вид −(−x) откуда получим просто x

Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
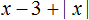



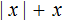
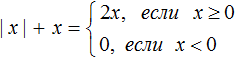
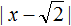
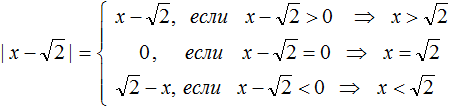


давно ждала нового урока. скоро ли будет следующий?
Если все пройти это какой класс?
Наконец-то, надеюсь следующий урок не через год. Пожалуйста
Круто что проект не умер. Спасибо вам большое
Отдельное вам спасибо за ваши уроки которые выкладываете, только побыстрее бы выходили уроки т.к скоро ЕНТ.
сколько набрал? я просто тоже подтягиваю математику из-за ЕНТ.
оо я тоже сдаю ент. я вообще не понимаю математику,поэтому и подтягиваю
Ууура, новый урок. Я уже подумал что вы закинули проект. Долго ждать новые туториалы?
Ураааа, 70!!! Но очень уж долго, но спасибо!
Огромное спасибо.
Pforzheim. Германия.
Невероятно рад что проект всё ещё развивается и появляются новые уроки! Для дурачков, которые в школьные годы забили на математику, подобный курс просто бесценный! Спасибо большое
Дурачки плюсуют
++++++
Карл, ОН ВЫШЕЛ!
Ура! Мне давно надо было разобраться с модулями. И вот они модули. Отлично!
Похоже в решении задания 4 есть пара ошибок.
>> Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу.
Надо бы поправить: расстояние между СОСЕДНИМИ целыми числами равно одному шагу.
Сначала было непонятно, пришлось перечитать. Не недооценивайте то, что поначалу кажется простым)
Здравствуйте,когда будут новые уроки?
Очень хороший проект. Как будет возможность поддержать материально – сразу сделаю
Объсните 5 тую задачу пожалуйста.
Ого, я думал автор забыл про проект) Очень рад, что вы вернулись.
Спасибо за очень доступное изложение материала. Ждем ещё урок про функции.
“Преобразование выражений с модулями
Пример 1.
Если |x| < 0, то получим −3x − 2x + 5y, откуда −5x + 5y. Вынесем за скобки множитель −5, получим −5(x − y)" – здесь мне кажется ошибка!
По моей логике модуль |x| < 0 не может быть меньше нуля. Меньше нуля может быть подмодульное выражение x < 0. Следовательно должно быть так:
Если x < 0, то получим
−3(-x) – 2(-x) + 5y;
3x + 2x + 5y;
5x + 5y;
5(x+y).
В качестве проверки я подставлял разные числа вместо x и y в полное уравнение, до того как были проведены тождественные преобразования. И там у меня тоже результаты не сходились с выражениями которые вы получили после тождественных преобразований.
Тот же раздел, Пример 2. По моей логике так при любом раскладе будет получаться -х.
Пример 2. Раскрыть модуль в выражении: −|x|
Для наглядности будем подставлять туда 2 и -2. И использовать явно выраженный коэффициент перед модулем.
-1|2| = -1 *2 = -2
-1|-2| = -1 * (-(-2)) = -1 * 2 = -2
В обоих случаях мы получили отрицательное число.
Круто,но вот новые уроки уже давно не выходили
Зачем у двойки два минуса во втором выражении?
-|x| это -1*|x|, если x < 0, значит модуль раскрывается со знаком минус, с одним, а не с двумя, следовательно -1 * (-2), зачем вы еще один минус добавили, непонятно
Всем привет! Можете подсказать, данная программа какого класса?
8 класс
Можете ответить, а этих знаний хватит чтобы сдать ЕГЭ по профильной математике?
Если реально хотите помочь автору, то минимум, что можно сделать – это отключить адблок при просмотре уроков. Мелочь, конечно, если это сделает один человек, а вот если каждый, то хоть что-то накапает автору от Яндекса и Гугла.
Здравствуйте, алгебра также входит сюда?
А разве если x=0, то в выражении
|x|÷x=решений нет?
Наверное правильнее сказать, что частное от деления нуля на ноль неопределённо, имеет бесчисленное множество решений, не имеет смысла без указания дополнительных данных. Но нельзя сказать, что решений нет.
Сколько набрали?
В шк на скок учили матем?
Можно уроки о синусов и косинусов
Сделайте пожалуйста урок про Эйлера Венна и его диаграммы.
Админ, здравствуйте, у меня вопрос, будут ли новый уроки?
Добрый вечер!
Это очень доступный, удобный и лучший сайт для изучения математики. Только жалко, что нет новых уроков. Все мы ждем новых уроков и прекрасных объяснений. Такую работу хорошую начали. Будут ли новые уроки???
Здравствуйте, подскажите, пожалуйста, почему в примере 1, параграфа “Преобразование выражений с модулями” в случае х < 0 имеем −3x − 2x + 5y", а не −3x + 2x + 5y? Ведь в случаее x < 0, коэффициент -2 перед и -x при умножении должны дать 2, т.к -1 на -1 = 1?
"Раскроем модуль в получившемся выражении. Если x ≥ 0, то получим 3x − 2x + 5y, откуда x + 5y.
Если x < 0, то получим −3x − 2x + 5y, откуда −5x + 5y. Вынесем за скобки множитель −5, получим −5(x − y)"
Здравствуйте. Мы же просто раскрываем модуль. В остальных местах отрицательный x просто подставится куда нужно.
Возьмите например значения x=−2 и y=1. Подставьте их сначала в выражение 3|x|−2x+5y, а потом в −3x−2x+5y
Добрый день! Спасибо за уроки, все понятно и трудностей не возникает
В последнем примере ошибка:
-|-x| при x > 0 = -(-(-x)) = -(x) = -x, а в примере x без минуса
Все правильно. Если бы вместо х было поставлено -х тогда когда мы бы внесли минус какой то число то это было бы: -(-какой то число) и те две минусы закрылы бы самих себя оставляя позитивную числу