Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение 
равно отношению 
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции выполнить деление в обеих дробях, то получится число 2 в обеих частях:
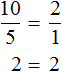
Предположим, что в классе 10 девочек и 5 мальчиков
Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки
Теперь рассмотрим другой класс в котором две девочки и один мальчик
Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:
Можно сделать вывод, что отношение пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам
а также отношение 12 девочек к 2 мальчикам
Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что 
, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение 
не пропорционально отношению 
.
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию 
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
2 = 2
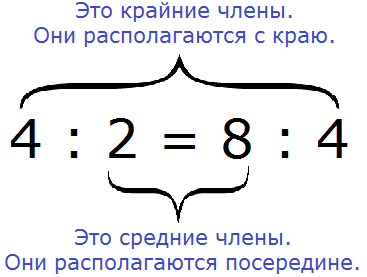
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции крайние члены это 4 и 4, а средние члены это 2 и 8
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
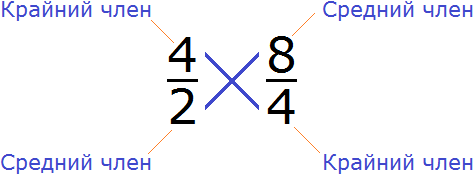
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция 
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
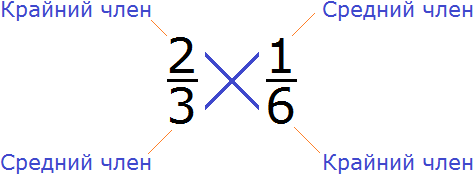
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция составлена неправильно.
Поэтому в пропорции разумнее заменить знак равенства (=) на знак не равно (≠)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Спасибо, все очень доходчиво!
Спасибо за Ваши уроки!Как хорошо, что есть еще такие люди, которые бескорыстно помогают другим!
Спасибо за этот сайт . ОбЪяснения понятны… Прошёл 3 темы и всё понятно. Спасибо … Готовлюсь к экзамену.
Экзамену?:D. Лол,это же уроки для дошкольников-школьников начальных классов.
Не смешно))) пропорции проходят в 6 классе. Почитайте учебник по математике — все настолько запутано и напичкано ненужными сведениями, которые запутывают еще больше, что только здесь можно разобраться самому и помочь разобраться детям
Здравствуйте! Большое спасибо за уроки
Не могли бы вы объяснить, почему в пропорции члены называются крайними и средними?
Потому что ,крайние члены в краю уровнения,а средние члены в середине ближе к ровно.
Пример: 4:2=8:4.
4 и 4 это крайний член,а 2 и 8 это средние члены
Как это можно использовать в реал. жизни?
зависит от того чем занимается человек
Если думать о пропорциях или о других математических вещах отдельно от реальной жизни — то практически никак. Ищите в жизни математические законы и информацию, которую можно подогнать под пропорцию или что ещё. Подобно тому, как вы из задачи на уроке извлекаете суть, отсекая всё лишнее (яблоки, бочки, километры, людей и т.п), оставляя лишь суть — цифры. Вы же понимаете, что вам нужны только цифры для подсчёта, а не конкретные сущности в виде вещей. Математические законы говорят как работать с этими цифрами, а сами цифры должны выбирать вы сами. Зашли в магазин, увидели стоимость товара, помножили на количество — вот и пригодилась базовая арифметика. Нужно найти применение пропорции? Выдёргивай для неё цифры из мира вокруг и применяй. А откуда брать цифры для неё — решать тебе в каждом конкретном случае.
И ещё: никогда не дели на ноль! XD
Даже для того чтобы приготовить еду необходимы пропорции, разбавить краску для волос, приготовить цементную смесь или гипсовую и так далее. Самое важное в том,что данные знания формирует основу для получения новых навыков. И так во всем. Не отказываетесь от любых знаний, даже, если вы думаете, что они не так важны, это, прежде всего опыт, а опыт даёт большие возможности для самореализации.
Например, расчет технологических карт в кулинарии.
Большое спасибо вам за ваши старания и помощь людям в изучении математики. У вас всё замечательно выходит, очень понятно и без косяков, которые могли бы сбить с толку.
Огромное Спасибо!!
Спасибо! Очень доступно!
Что такое «неправильная пропорция»? Уж коли есть пропорция, то она правильная априори. «Неправильная» просто пропорцией не является. А в остальном наглядно и доступно.
Запас двухметровых дров пильщики распилили на полуметровые дрова за 4 часа 30 мин. За какое время тот же запас дров они распилили бы на сорокасантиметровые дрова? Ребята помогите решить эту пропорцию.
4/3 = 6/4,5
Пожалуйста, по подробнее как так вышло?
Виктория, это задача на пропорциональность. Изучив только пропорцию, решить эту задачу не получится. Нужно ещё изучить прямую и обратную пропорциональность и задачи по этой теме. Почитайте, темы не сложные.
Если двухметровые дрова распиливать на полуметровые, то надо делать три распила на полене. А если те же дрова распиливать на 40-сантиметровые, то надо делать четыре распила на полене. С увеличением количества распилов, увеличивается время выполнения работы с 4 ч 30 мин до 6 часов.
ps, 4,5 это 4 часа 30 минут
Это можно вычислить исходя из правила произведение крайних равно произведению средних. То есть если неизвестен крайний то умножаем два средних и делим на известный крайний. И наоборот если неизвестен средний то умножаем два крайних и делим на известный средний.
Спасибо!
большое спасибо за такой доходчивый урок.я,уже не молодой человек,но так хочется помочь своему внуку,обязательно буду пользоваься вашим сайтом .еще раз большое спасибо
люблю этот сайт
большое спасибо всё очень доходчиво спасибо за сайт хороший сайт если бы не этот сайт то я бы не знал спасибо большое очень молодцы этот сайт меня выручил ещё раз спасибо.Всем пока!
Увы давно тут новых уроков нет. Тут я многому научился.Спасибо вам большое.
Кстати если кто-то дальше хочеть учиться и знает английский то советую сайт https://www.khanacademy.org/math/algebra/ , вдруг кому-то понадобиться 🙂
Ждём новых уроков.
Здравствуйте. Я думаю, что имеет смысл добавить нахождение неизвестного члена пропорции.
Между прочим самые большие пробелы это пробелы в школьной математике… И чем раньше, тем хуже! И восполняются они крайне сложно и долго… Вам по сути придётся с момента первого пробела всё заново изучать потому что остальное вы изучили неправильно, без учёта этих знаний. Каждый такой пробел будет оч сильно влиять на все ваши знания и главным образом на понимание. Поэтому не будьте наивны… Изучайте всё хорошо и внимательно! Школьная математика имеет очень большое значение ка фундамент всего образования. Вы никогда не научитесь делать сложные вещи если не будете понимать простых заложенных в их основе. Более того, этого вам больше никто никогда не будет объяснять потому что предполагается что вы всё это знаете и хорошо понимаете. Успех учёбы в Вузе во многом определяется хорошими знаниями школьной программы. Вам каждый такой пробел придётся восполнять самим с большими усилиями и бол кол-вом времени… Вы скоерй всего не сможете учиться в вузе… Я такую картину наблюдал многократно. Это оч страшно когда человек не понимает простых вещей…
Отношение эквивалентности на самом деле это в математике. Пропорции это переформулировка.
Затрачивая на изготовление каждой детали 2/3
мин, бригада выпускала за смену 540 деталей. Сколько деталей будет выпускать за смену бригада, если на изготовление каждой детали будут затрачивать 3/5
мин? На сколько процентов повысится при этом производительность труда?
Решение
Пусть x − количество деталей, которое будет выпускать за смену бригада, если на изготовление каждой детали будет затрачиваться 3/5 мин.
Составим и решим пропорцию:
2/3:3/5=х:540
х=540∗2/3:3/5=540∗2/3∗5/3=60∗10=600
деталей будет выпускать бригада за смену при новой производительности.
Не понимаю почему так составлена пропорция, ведь 2/3 относится к 540. Должно же быть 2/3:3/5=540:х. Получается меньше 540. Может нужно в условии задачи изменить на изменится производительность а не увеличится?
Добрый день,
Так как 3/5 меньше 2/3, т.е. теперь на 1 деталь будет тратиться меньше времени — то пропорция должна быть обратной: 2/3:3/5=х:540 — у вас всё правильно было написано в первый раз)
Раз на деталь нужно меньше времени, то количество изготовленных за смену деталей вырастет — получается 600 деталей.
Чтобы правильно составить пропорцию нужно понимать что остается неизменным, в данном случае это время смены, а оно равно произведению скорости изготовления одной детали (шт/мин) и количества деталей (шт), получается 2:3∗540=3:5∗х
Важно ли учить пропорции и соотношение?
Спасибо. Это идеальный сайт для нас. Чётко и понятно все изложено