При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.
При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 – это множимое, число 2 – множитель, число 6 – произведение.
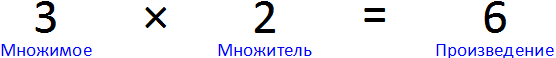
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
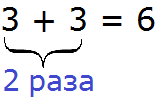
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим например 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b – сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
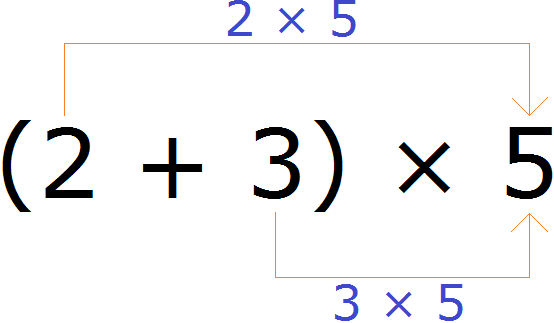
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: “увеличить ноль в два раза”. Но как можно увеличить ноль в два раза, если это ноль? Никак!
Иными словами, если “ничего” увеличить в два раза или даже в миллион раз, всё равно получится “ничего”.
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. В таких случаях применяется следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить множимое 2. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
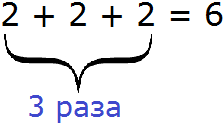
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
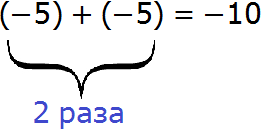
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, а (−5) отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях применяется следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
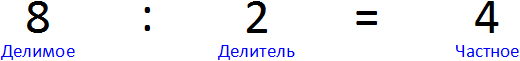
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
![]() , при b ≠ 0
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3

Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3

(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
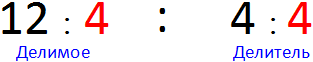
(12 : 4) : (4 : 4) = 3 : 1 = 3
Снова получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 – положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Спасибо
можете пожалуйста объяснить почему в выражении (-4)*(-2) получается положительное число 8 а в выражении (-2)*(-3)*(-4)получается отрицательное число -24
Потому что если, к примеру, два, четыре, шесть минусов, то они всегда будут доават плюс. Т. Е в ответе всегда будет +.
А если три минуса, пять, семь, то в ответе будет –
смотри просто в этом выражении 2 действие 6 разделить на отрицательное число -4 а при умножении на разные знаки в итоге будет – надеюсь норм объяснил
Смотрите,-2•-3 даёт положительное число,т.е. +6.
+6 умножаем на (-4) и получаем отрицательное число.
я внимательно ещё раз посмотрел на выражение и всё понял почему именно так, спасибо за ваши уроки они очень помогают.
Огромное спасибо!!!
Сппсибо за ваши уроки. Но примеры по теме деление и умножение отрицательных чисел не очень убедительны, я так и смог представить как это какое либо число, например (-2) взять по (-2) раза. И у вас противоречие в формулировках, вы говорили, что если есть знак +, то всегда идет смещение правее, но в выражени (-2)+(-5)=-7, смещение по координатной прямой происходил влево
В выражении (-2)+(-5) сначала нужно раскрыть скобки, чтобы можно было двигаться влево или вправо. Получится -2-5, где смещение идет влево – попадаем в точку -7.
Разность -2-5 преобразована в алгебраическую сумму (-2)+(-5), чтобы обосновать правила сложения отрицательных чисел.
В некоторых задачах перемножаются отрицательные числа, где принцип работы умножения такой же, как и в случае с положительными числами. Подробнее в простейших задачах по математике.
А можно понимать движение по координатной прямой так?
Прим: -5 +( -5) Я смотрю на точку -5, плюс показывает, что двигаться нужно —-> но на «отрицательное расстояние» т.к это не возможно направление как бы инвертируется. И отрицательное расстояние на самом деле указывает на то , что направление меняется. Есть ли в этом смысл?
Серго
-5 +( -5) – мы шагаем (складывая шаги) в отрицательную сторону.
Знак плюс в данном случаи с отрицательными числами не указывает в каком двигаться направление, он указывает, что числа надо сложить и добавить потом перед числом минус.
9 : (−3) = −(|−9| : |−3|) почему знак 9 изменился на модуль |-9| ? если он должен (|9|*|-3|) ? В итоге число + должно получиться а не –
Да, опечатка была. Спасибо, исправил
Попытался представить варажение (-4)*(-2)=8 на координатной прямой, но так и не удалось. Я так понял, что это невозможно представить или я ошибаюсь?
Неплохие у вас уроки в целом, занимаюсь с первого урока.
В некоторых уроках очень трудно информацию сжать для конспекта.
Вы так сильно всё усложняете, то что можно объяснить тупому барану за 5 минут вы расписываете на 30 .
Олег, вы оставляете не первый негативный комментарий к урокам на данном сайте с небольшим промежутком времени. При этом комментарии не содержат конструктивной критики и являются отзывом в стиле «на этом сайте все для дураков, а я умный.» Ваши действия вызывают обоснованные подозрения в том, что вы представитель платного образовательного сайта, заинтересованного в дискредитации прекрасного образовательного материала, который позволяет не подготовленным людям без преподавателя самостоятельно разобраться в базовых необходимых вещах. Оставляя за рамками возможные недостатки материала, напоминаю вам 1) материал позиционируется как математика с нуля, поэтому многие простые вещи здесь объясняются очень подробно и максимально доступно, а не сухо ужаты в несколько строк 2) материал абсолютно бесплатный, добровольные пожертвования — это личное решение каждого. Я вот давно занимаюсь по данному сайту и перечислил пару сотен в качестве благодарности. Неподготовленным людям достаточно взять популярный учебник по математике за 5 класс и попробовать позаниматься по нему. Очень скоро математика будет заброшена в большом количестве случаев, а данный сайт позволяет изучить все базовые вещи с гораздо меньшим количеством усилий. 3) данный сайт не входит в обязательный материал, принудительно навязываемый министерством образования. Его посещение сугубо добровольное. Поэтому желаю вам успехов в изучении математики в других местах, я верю в вас . Я не имею никакого отношения к создателям материала, а просто пользуюсь им и читаю все комментарии после уроков. Как раз дошёл до этого урока и предыдущего и узрел ваши комментарии. После второго комментария я понял, что вы преследуете нехорошие цели.
Более понятное объяснения -https://www.youtube.com/watch?v=GERNxLLfwGM
Получается в математике есть фундаментальная ошибка:
(+2)*(+2) = 4
(-2)*(-2) = 4 – это выражение ложное
(-2)*(-2) = -4 – должно быть так, или в противном случае выражение (+2)*(+2) должно возвращать отрицательное число (+2)*(+2) = -4
Если минус на минус даёт плюс, то плюс на плюс даёт минус?
Плюс на Плюс дает плюс)))
2+2=4
Получается в математике есть фундаментальная ошибка:
(+2)*(+2) = 4\n
(-2)*(-2) = 4 – это выражение ложное\n
(-2)*(-2) = -4 – должно быть так, или в противном случае выражение (+2)*(+2) должно возвращать отрицательное число (+2)*(+2) = -4\n
Если минус на минус даёт плюс, то плюс на плюс даёт минус?
P.S. что то в предыдущем комментарии все переводы строк исчезли и получилась каша.
Получается в математике есть фундаментальная ошибка:
(+2)*(+2) = 4 *перевод строки \n*
(-2)*(-2) = 4 – это выражение ложное*перевод строки \n*
(-2)*(-2) = -4 – должно быть так, или в противном случае выражение (+2)*(+2) должно возвращать отрицательное число (+2)*(+2) = -4*перевод строки \n*
Если минус на минус даёт плюс, то плюс на плюс даёт минус?
P.S. что то в предыдущем комментарии все переводы строк исчезли и получилась каша.
Немного подзабыла- если стоят слева направо сначала деление, потом умножение, то таков и порядок действий, или же сначала умножение потом деление?
Слева на право делают те действия, которые идут по очередности, если в примере присутствуют, только умножение и деление :
3*4:3=4
1) 3*4=12
2) 12:3=4
12:4*3=9
1) 12:4=3
2) 3*3=9
мне одному кажется странным представленное доказательство того что (-4)*(-2)=8? по сути оно сводится к тому что это произведение равно 8ми потому что 8-8=0… при условии что (-4)*(-2)=8. бред какой то.
Согласен с вами
может кому поможет, если сомневаетесь, какой знак ставить.
враг моего друга – мой враг
враг моего врага – мой друг
друг моего врага – мой враг
друг моего друга – мой друг,
где враг – отрицательное число, а друг – положительное 🙂
Первая часть уже проходилась в начальных уроках, а так в принципе сверху скинули видео, с ним реально будет быстрее. Погнали дальше.
СПАСИБО ЗА УРОКИ СЕЙЧАС ПОНИМАЮ МАТЕМАТИКУ АВТОР ДАЙ БОГ ВАМ ЗДАРОВИЕ, ТО ЧУВСТВО КОГДА В ШКОЛЕ УЧИТЕЛЬНИЦА НЕ ЧЕГО НЕ УЧИЛА
Олег, очень жаль, вижу, что вы ничего не поняли.