В данном уроке мы рассмотрим такие понятия как делители и кратные.
Что такое делитель?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:
8 : 2 = 4
Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:
9 : 3 = 3
Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:
10 : 4 = 2 (2 в остатке)
Определение. Делителем числа а называется число, на которое число а делится без остатка.
Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 12 и прочитаем определение:
Делителем числа 12 называется число, на которое 12 делится без остатка.
Попробуем перечислить эти числа:
1, 2, 3, 4, 6, 12
Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Кратные числа
Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3
6 : 3 = 2
Определение. Кратным числа а называется число, которое делится без остатка на а.
Данное определение содержит переменную a. Подставим вместо этой переменной любое число, например число 5 и прочитаем определение:
Кратным числа 5 называется число, которое делится без остатка на 5.
У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Примеры:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Примеры:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
27 : 3 = 9
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
18 : 9 = 2
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
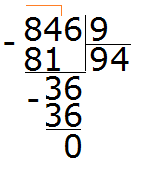
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
20 : 2 = 10
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
5 : 1 = 5
5 : 5 = 1
Значит, число 5 является простым числом.
Составным же называется число, которое имеет больше двух делителей. Например, число 4 составное, поскольку у него больше двух делителей: 4, 2 и 1
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
Значит, число 4 является составным числом.
Разложение составного числа на простые множители
Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.
Например, число 6 можно записать в виде суммы 4 + 2 или в виде частного 12 : 2 или в виде произведения 2 × 3. Последнюю запись 2 × 3 можно назвать разложением числа 6 на простые множители.
Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.
Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4
4 = 2 × 2
Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6
6 = 2 × 3
Разложим на множители число 8. Это число можно разложить на множители 2 и 4, при этом множитель 4 можно разложить на два множителя: 2 и 2. Поэтому вместо четвёрки записываем её разложение:
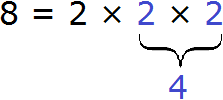
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10
180 = 18 × 10
Теперь раскладываем множители 18 и 10 на другие множители:
18 = 3 × 6
10 = 5 × 2
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:
6 = 2 × 3
Теперь собираем все простые множители вместе:
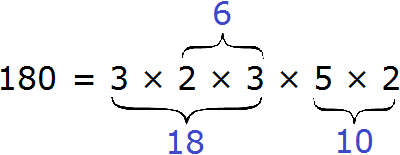
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.
Например, разложим предыдущее число 180 этим способом.
Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
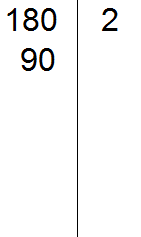
Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.
90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:
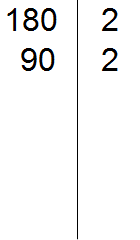
Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:
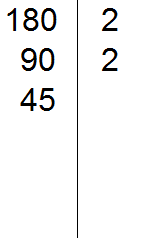
Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
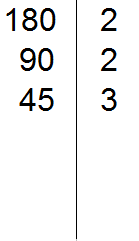
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
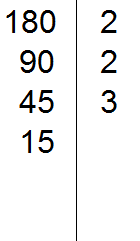
Теперь делим 15. Проверяем делится ли 15 на 2.
15 не делится на 2. Тогда проверяем делится ли 15 на 3.
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
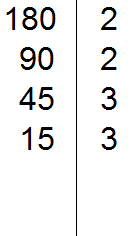
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:
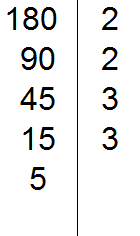
Теперь делим 5. Проверяем делится ли 5 на 2.
5 не делится на 2. Тогда проверяем делится ли 5 на 3.
5 не делится на 3. Тогда проверяем делится ли 5 на 5.
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:
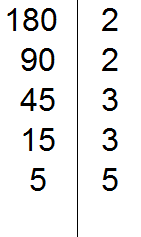
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:
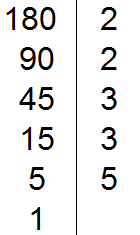
На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.
Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
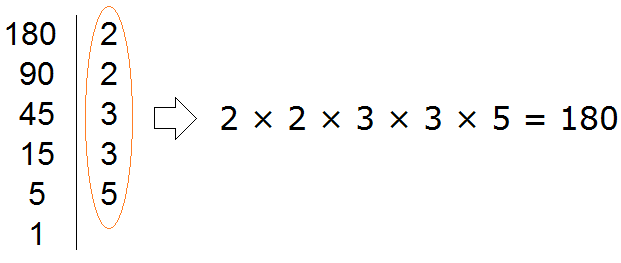
Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
Пример 1. Найти делители числа 12
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
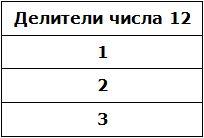
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
2 × 2 = 4
Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
- записать в качестве первого делителя единицу;
- разложить исходное число на простые множители и выписать из полученных простых множителей те множители, которые являются делителями исходного числа (если множитель повторяется, то выписать его нужно только один раз);
- найти все возможные произведения полученных простых множителей между собой. Получаемые в результате ответы будут остальными делителями исходного числа.
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
1
Теперь разложим число 6 на простые множители:
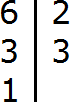
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
Теперь найдём все возможные произведения простых множителей числа 6. В данном случае имеется только одно произведение, а именно 2 × 3. Это произведение равно 6. Допишем число 6 к нашим делителям:
1, 2, 3, 6
Таким образом, делителями числа 6 являются числа 1, 2, 3, 6.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
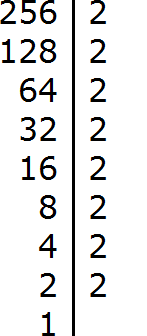
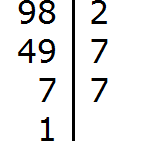
Разложить на множители 512 , подстава.
Разложи 2 по девять раз.
512=2x2x4x2x2x2x2x2
а 4 что не разложил? :з
Потому что число 4 не простое, а раслкладывать можно только на простые числа, то есть простые множители.
Раскладывать можно НА простые числа, а 4 это то число, которое раскладывается. Оно составное, и поэтому разложить его можно.
Ещё какая, чувак, особенно после 256))) Админы тролли математики
512:2=256:2=128:2=64:2=32:2=16:2=8:2=4:2=2:2=1.
нет я ошибся .
512 | 2
256 | 2
128 | 2
64 | 2
Нет подставы)
512 это 2^9, то есть нужно сабж разделить на два девять раз.
Доброго времени суток! Во-первых, спасибо за сайт, доходчиво. Мне примеров не хватает, сама придумываю. Так например, помогите ПЖЛ разложить на простые множители число 119. Спасибо!
7*17=119
больше ни как
Прошло 4 года,но я отвечу , 7×3×3×3
Прошел год, но я отвечу, 7×3×3×3 = 189, а нужно 119
Прошло пол года, но я отвечу 119:7=17:7=1
Прошло пол месяца, но я отвечу: спасибо за внимание!
Прошёл год, но я отвечу: 119:7≠17≠1
Прошёл 9 месяцев но я отвечу 119:7
17:17
1
Спасибо вам большое за этот сайт! Это просто такая находка! У меня экзамены через 4 месяца, а я в математике не очень, знания на уровне 6-7 класса, а ваш сайт ооочень помогает) Спасибо большое! Продолжайте в том же духе, надеюсь, что мой отзыв Вас как-то подбодрит, дорогие разработчики)
Админам привет! В этом году у меня ЕГЭ, а математику я знаю… ну почти незнаю. Решил подучить, сайт — находка. Спасибо огромное за такую работу.
Очень доходчиво,с ясными примерами,такой подход прививает любовь к предмету ,спасибо!
а как можно решить 512?
512 это 2×9
2x2x2x2x2x2x2x2x2=512
2х9=18
Вы имели ввиду 2^9 или 2х2 9 раз
скорее всего он имел ввиду 2 в девятой степени
2^9 или 2×2 9 раз и есть 2 в степени 9…
всё решил!
извините!!! Спасибо большое за сайт вам! Отличная работа ребята. Желаю вам удачи и хорошего настроение
Я конечно понимаю, что сижу на халяву и с большой легкостью учу математику, которую не мог понять в школе… Но пожалуйста? продолжайте выпускать новые уроки, нигде нет таких доступных объяснений. Куда подписаться, или есть кошелёк для поддержки проекта? Спасибо за помощь в образовании нации <:-)
Большое человеческое спасибо!!! Очень нужная и важная работа.
Всем привет! Решая с дочкой пример 6 класса, я не смог в голове найти число кратное 45. Нужно найти все комбинации чисел *34* кратные 45. Методом перебора, через excel, я быстренько нашел эти числа: 2340 и 6345. Но это комбинаций немного, а если будет найти все комбинации чисел **34** (или ***34***) кратных 45, что тогда делать. Должно же быть логическое решение данных вариантов, голова не компьютер, все числа просчитывать.
зы. Извините если я не по теме.
Должны выполняться сразу 2 признака делимости — на 9 и на 5
98 ведь можно можно разложить как
98 | 2
49 | 2
24 | 2
12 | 2
6 | 2
3 | 3
1 |
Leon, у вас ошибка во второй строке — 49 на 2 без остатка не делится, т.к. будет 24.5
Когда мы хотим разложить число 98, то правильнее было бы сказать — разложить на ПРОСТЫЕ множители. При разложении пользуемся признаками деления на 2,3 и 5.
1) в числе 98 последняя цифра 8 — четная, и, значит, пользуемся признаком деления на 2.
98:2=49
2) число 49 на 2,3 и 5 не делится, а вот следующее простое число 7 является делителем для 49 :
49:7=7
3) 7- это простое число. Следовательно, оно делится только на 1 или 7:
7:7=1
На этом разложение на простые множители числа 98 завершено, и его результат:
98=2×7×7
Все доходчиво и понятно, спасибо!
Ясно, только не понятно пока где это может пригодится?
Кстати я такой большой комент написал, почему то ошибку выдает, не хочет на сайт закоментить 🙁
Здравствуйте!Админ.
Спасибо за сайт.
Подскажите как можно быстрее сложить и вычесть цифры в уме.
Программирование
Можно задам вопрос? Достаточно ли здесь знаний для того чтобы изучать химию?
неть 🙁
сайт очень классный! Единственное, чего я тут не нашёл, так это взаимно простые числа:(
(ученик 6-го класса)
или это не здесь надо искать?
Из однозначных чисел чётными являются числа 0, 2, 4, 8,
Вы пропустили 6
А также: -2; -4; -6; -8
А если число изначально простое, например 2971, как это понять сразу?
Или вот допустим число 973
973 | 7
139 | ?
139 — простое число, но сколько же времени уйдёт, если делить его снова и снова?
Для больших чисел сразу нельзя сказать, что оно простое или составное. Нужно исследовать их, прибегая к различным способам и тестам. Они здесь не рассмотрены ввиду своей сложности и малой распространённости. Можете на досуге почитать об этом здесь.
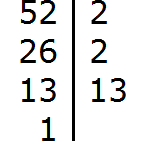
А в смысле? В последнем примере, а именно где нужно разбить на простые множители число 228. Сначала решаешь-решаешь.
228|2
114|2
57|?
Вы говорили, что считаем сумму. То есть, в данном случае сумма 5 + 7. Будет 12. Но 12 елится на 2. Но 57 не делится на два.. Я конечно попробовала следующее число и у меня все получилось, но что насчет вот этой ситуации? Получается, не всегда с помощью этой «суммы» можно подобрать, узнать число?
Сумму считаем только в том случае, когда проверяем делится ли число на 3 или на 9.
Если вы хотите проверить делится ли число на 2, то сумму считать не нужно. Нужно посмотреть оканчивается ли число нулем. Если оканчивается нулём, значит число делится на 2.
Либо можно посмотреть является ли число, которое вы хотите разделить, чётным. Если число чётно, то оно делится на 2. Чтобы распознать четное число, можно посмотреть на какую цифру оканчивается это число. Чётное число оканчивается чётной цифрой.
Замечательный сайт! Организаторы большие молодцы! Было бы полезно после каждого шага добавлять побольше практики из задачников.
Спасибо за Ваш труд!
Здравствуйте!
Я попала на Ваш замечательный сайт, по тому же вопросу, что задавал Александр. В четырехзначное число, надо добавить правую и левую неизвестную цифру, чтоб оно (число), было кратно 45. Это задание для детей, начало 6 класса. Правило не нашла(( Может быть поможете?
Должны выполняться сразу 2 признака делимости — на 9 и на 5.
Здравствуйте. Хочу поделится признаком делимости на 2.
Признак: если у двузначного числа в десятках нечетное число а в единицах четное, то оно делится на 2.
И это относится не только к двузначным числам, если у числа в единицах четное значение а у старших разрядов нечетное, то каким бы большим это число не было оно поделится на 2.
Попробуйте.
P/S у компьютера максимально допустимое значение примерно 9 223 372 036 854 775 807 если вы попробуете посчитать число больше этого, ответ будет некорректным
Плохой признак делимости, так как 22 (в десятках чётное) кратно двум.
Любое число с чётным окончанием является чётным, так как чётное окончание свидетельствует о том, что число было получено умножением двойки или других чётных чисел.
здравствуйте,а книги продается? просто очень замечательный сайт,мне очень помогли, думал никогда не полюблю математику,благодаря вашему сайту мне удалось
Здравствуйте. Я хотел бы поинтересоваться, а как логическим путем дойти до правила, что число делится на 3, если сумма цифр этого числа делится на 3? Или это правило выведено лишь экспериментальным путем? Почему оно не действует на другие числа?
Здравствуйте.
Это всё из теории чисел — отдельного раздела математики. Правила выводятся путем доказательства теорем. Можете почитать об этом на досуге.
здравствуйте объясните пожалуйсто это выражение
( − 2)2 + 4 =
здравствуйте объясните пожалуйсто это выражение
( − 2)2 + 4 =
Минус два умножить на два и прибавить четыре.
(−2) × 2 + 4 = −4 + 4 = 0
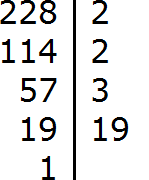
Почему при нахождении простых множителей числа 228 первым простым множителем выступает 2, а не 3? Ведь 228 не оканчивается нулём, а сумма чисел из каждого разряда даёт уверенные 12 единиц, которые делятся на три.
Признак делимости не всегда нужно использовать или я чего-то не понимаю?
Оканчивание нулём это один из признаков деления на 2. Есть и другие признаки. Например, если число чётное, то оно делится на 2. В данном случае как раз использован этот признак. Двойку в качестве простого множителя желательно проверять в первую очередь. Ну ничего страшного, что в качестве первого множителя вы выбрали тройку. Итоговое разложение всё равно будет верным.
Разве простым числом считается деление на себя и на единицу без остатка? Тогда не все ли числа простые? Думаю, здесь нужно поставить одно условие — ТОЛЬКО. И тогда формулировка будет звучат так — число является простым, если оно делится ТОЛЬКО на само себя и на единицу, других целителей у него нет.
Если это правильно, то исправьте пожалуйста. Спасибо.
Thank you
У меня вопрос, а как называть b, делитель и делитель? В выражении 15:4 15- будет делимое, а 4ка делителем, как это было в прошлых уроках, почему к примеру если вместо 4ки там была бы 5ка её назвали бы так же делителем? А если 4 не делитель, то как вообще его называть?
4 тоже делитель, но в этом случае добавляется остаток r.
a : b = c (r в остатке)
15 : 4 = 3 (3 в остатке)
a = 15 (делимое)
b = 4 (делитель)
с = 3 (частное)
r = 3 (остаток)
a = b * c + r
15 = 4 * 3 + 3
Афтор молодчинка
А кто знает почему умножение и деление решили выполнять до сложения и вычитания? Какая причина не оставлять оставлять обычный порядок?
Потому что деление и умножение соответствует многократному сложению или вычитанию. Например, 10:2=5 это (10-2) 5 раз: 10-2-2-2-2-2=0. А 3х15=45 значит, что 3 надо взять 15 раз, или что 15 надо взять 3 раза: 15+15+15=45. Это «оптовые» действия. И если сперва выполнить сложение или вычитание, то изменится и условие «опта». Например: 1+10:2=11:2=5,5 вместо 1+10:2=1+5=6. Или 40+3х15=43х15=645 вместо 40+3х15=40+45=85.
Надеюсь, понятно объяснила)
Спасибо за годные уроки, продолжайте в том же духе!)
Народ, можете объяснить почему мы только находим простые множители у парных чисел, а примеру у числа 255 не можем? Потому что будет остача, ли по другой причине?
Интересно, почему в заданиях есть только те, где нужно найти простые множители, но нет заданий по нахождению всех делителей числа?
Спасибо !!!!
Наконец-то нашла где систематизировано и доходчиво!!!
Смогу обьяснить ребенку про Нок/Док)
Логически объясняю признак делимости на двойку: ноль на конце свидетельствует о том, что это число было умножено на десять или степень десяти, которые всегда раскладываются на два и пятёрку, соответственно, такое число тоже будет содержать двойки и пятёрки (а значит делиться на два и пять);
Выяснили, что любое круглое (с нулём на конце) число — чётное. Соответственно, второй признак делимости на два говорит о том, что если на конце (в разряде единиц) многозначного числа находится чётное число, то это число чётное.
Это потому, что любое многозначное число с чётным числом на конце можно представить в виде суммы круглого числа и чётного количества единиц. Соответственно, складываем чётное с чётным, что всегда даёт чётное число.
Здравствуйте, в последнем примере 228 я решила по-другому:
228| 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 |
Является ли данное решение верным?
Огромная благодарность автору за подробный разбор и бесплатный доступ!
Здравствуйте! Спасибо за сайт, это огромная работа!
Посмотрите, пожалуйста, нет ли ошибки: простое число = то, у которого 2 делителя, тогда составное число имеет ТРИ и более делителя? (в тексте написано «два и более» — но ведь два делителя — у простого числа).
Здравствуйте. Написали чуть понятнее.
Здравствуйте! Спасибо огромное за этот ресурс! Для самостоятельно изучающего математику с нуля взрослого, это просто находка. Пожалуйста, посоветуйте учебники с упражнениями и ответами, которые соответствовали бы излагаемому Вами материалу. Очень нехватает практики, и не просто найти подходящий материал. Возможно, у Вас уже есть сборник упражнений к этой программе?