Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.
Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.
А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.
Что такое дробь?
Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.
Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.

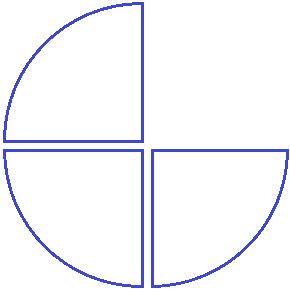
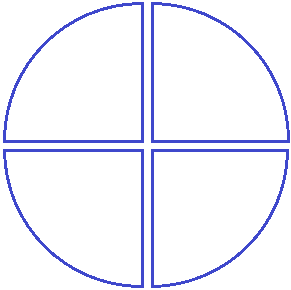
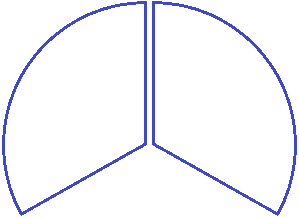
Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:
![]()
Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
![]()
А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
![]()
Такие записи называют дробями. Дробь состоит из числителя и знаменателя.
Число, которое записывается сверху, называется числителем дроби.
Число, которое записывается снизу, называется знаменателем дроби.
В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.
Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?
Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):
![]()
Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».
Теперь представьте, что пиццу мы разделили не на четыре части, а на три.

Допустим мы съели один кусок этой пиццы. Как записать такую дробь?
Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:
![]()
Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».
Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:
![]()
Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:

Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?
Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:
![]()
Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».
Дроби, которые мы сейчас рассмотрели, называют обыкновенными.
Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
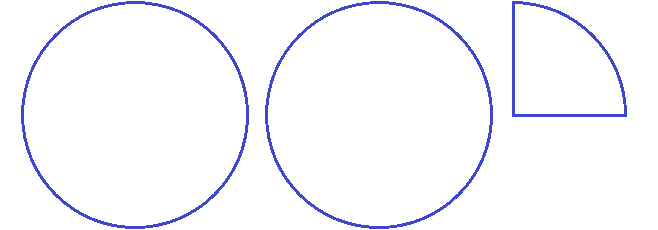
На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.
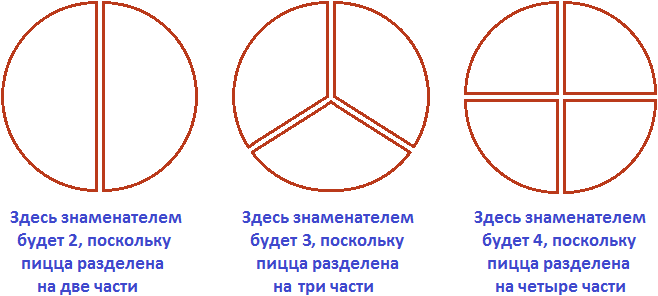
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли ![]() (одну часть из двух), или как говорят в народе «половину» пиццы.
(одну часть из двух), или как говорят в народе «половину» пиццы.
С помощью переменных дробь можно записать так:
![]() где a — это числитель, b — знаменатель.
где a — это числитель, b — знаменатель.
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
![]()
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём ![]() (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
(одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
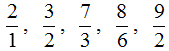 Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Теперь возьмём к примеру неправильную дробь ![]() и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:
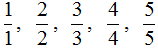
Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь ![]() . Применим её к нашей пицце.
. Применим её к нашей пицце.
Допустим, мы хотим съесть![]() пиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим эту
пиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим эту![]() пиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
пиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Дробь означает деление
Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь ![]() . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
. Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
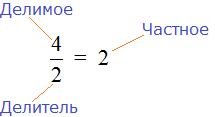
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
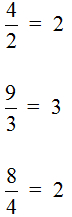
Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».
Выделение целой части дроби
Вычислим дробь ![]() . Пять разделить на два будет два и один в остатке:
. Пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Проверка: (2 × 2) + 1 = 4 + 1 = 5
Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:
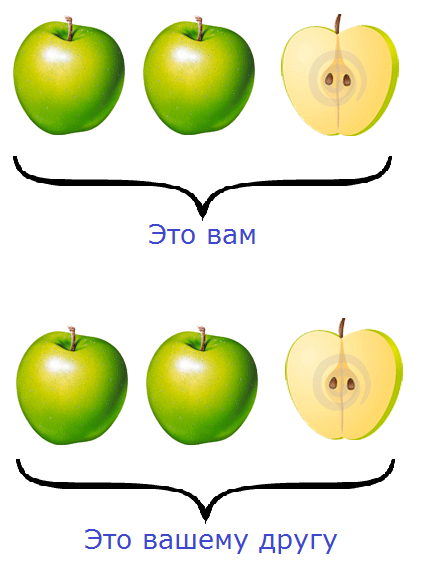
Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Теперь возвращаемся к дроби ![]() и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
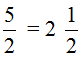
Схематически это выглядит так:
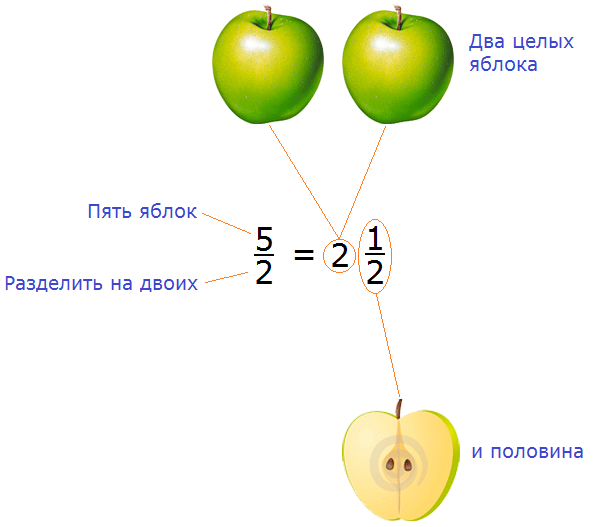
Процедуру, которую мы сейчас провели, называют выделением целой части дроби.
В нашем примере мы выделили целую часть дроби ![]() и получили новую дробь
и получили новую дробь ![]() . Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
. Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
В нашем примере целая часть это 2, а дробная часть это ![]()
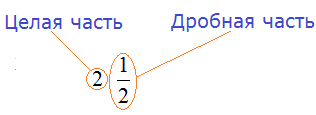
Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.
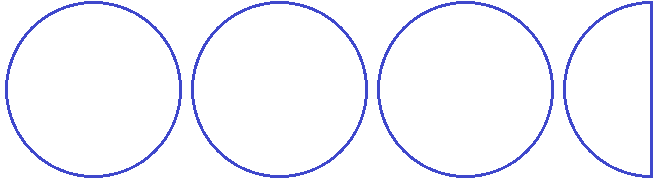
Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:
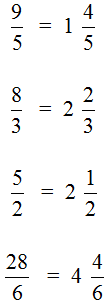
Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби ![]() . Записываем уголком данное выражение и решаем:
. Записываем уголком данное выражение и решаем:
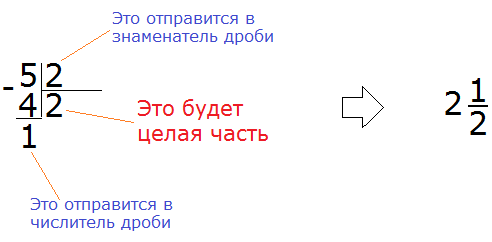
После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.
В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.
Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби ![]()
Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:

Получили: 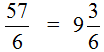
Перевод смешанного числа в неправильную дробь
Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь ![]() . Если выделить в ней целую часть, то получается
. Если выделить в ней целую часть, то получается ![]()
![]()
Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.
Например, переведём смешанное число ![]() в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
2 × 3 = 6
Затем к 6 прибавляем числитель дробной части:
6 + 1 = 7
Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:
![]()
Подробное решение выглядит так:
![]()
А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
![]()
Пример 2. Перевести смешанное число ![]() в неправильную дробь.
в неправильную дробь.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:
![]()
Основное свойство дроби
Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.
Например, рассмотрим дробь ![]() . Умножим её числитель и знаменатель на одно и то же число, например на число 2
. Умножим её числитель и знаменатель на одно и то же число, например на число 2
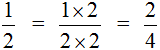
Получили новую дробь ![]() . Если верить основному свойству дроби, то дроби
. Если верить основному свойству дроби, то дроби ![]() и
и ![]() равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
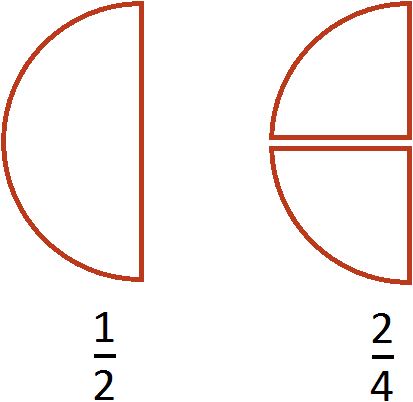
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь ![]() (один кусок из двух), а второй иллюстрирует дробь
(один кусок из двух), а второй иллюстрирует дробь ![]() (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
(два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями ![]() и
и ![]() можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
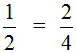
Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь ![]() . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
. Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
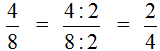
Получили новую дробь ![]() . Если верить основному свойству дроби, то дроби
. Если верить основному свойству дроби, то дроби ![]() и
и ![]() равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
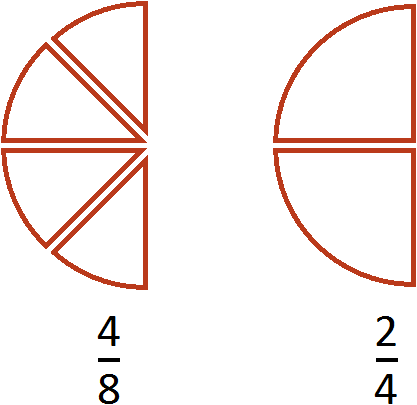
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь ![]() (четыре куска из восьми), а второй иллюстрирует дробь
(четыре куска из восьми), а второй иллюстрирует дробь ![]() (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
(два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями ![]() и
и ![]() можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
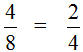
Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!
Сокращение дробей
Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь ![]() выглядит намного проще и красивее, чем дробь
выглядит намного проще и красивее, чем дробь ![]() .
.
Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.
Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.
Пример 1. Сократить дробь ![]()
Итак, нужно разделить числитель и знаменатель дроби ![]() на наибольший общий делитель чисел 2 и 4.
на наибольший общий делитель чисел 2 и 4.
В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби ![]() надо разделить на 2
надо разделить на 2
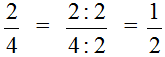
В результате дробь ![]() обратилась в более простую дробь
обратилась в более простую дробь ![]() . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.
. Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.
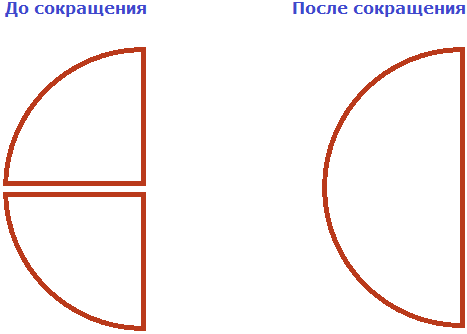
На рисунке представлены дроби ![]() и
и ![]() в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
Пример 2. Сократим дробь ![]()
Чтобы сократить дробь ![]() , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби ![]() на 20
на 20
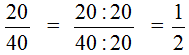
Пример 3. Сократим дробь ![]()
Чтобы сократить дробь ![]() , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби ![]() на 4
на 4
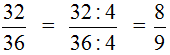
Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:
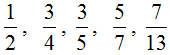
Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.
Второй способ сокращения дроби
Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.
К примеру, вернёмся к дроби ![]() . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
. Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
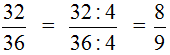
Теперь представьте, что в данном выражении отсутствует конструкция ![]() , и сразу записан ответ
, и сразу записан ответ ![]() . Получится следующее выражение:
. Получится следующее выражение:
![]()
Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.
Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:
![]()
Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:
![]()
Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36
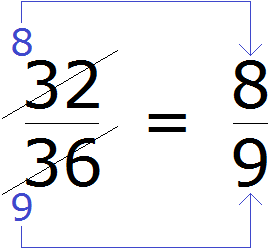
Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.
Например, сократим дробь ![]() , предварительно разложив на простые множители числитель и знаменатель:
, предварительно разложив на простые множители числитель и знаменатель:
![]()
Итак, мы разложили числитель и знаменатель дроби ![]() на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение: 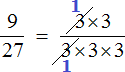
Сократить можно ещё по тройке в числителе и в знаменателе:
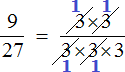
Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.
Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.
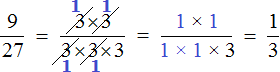
Получили ответ ![]() . Значит, при сокращении дроби
. Значит, при сокращении дроби ![]() получается новая дробь
получается новая дробь ![]() .
.
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.
Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:
![]()
Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:
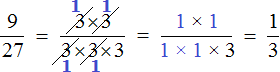
Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?
Задания для самостоятельного решения

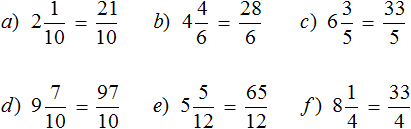
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже






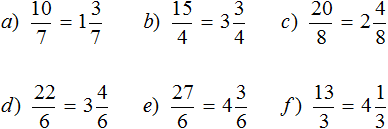



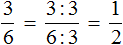
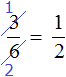
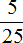
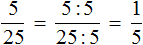

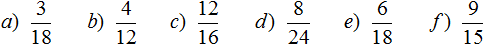
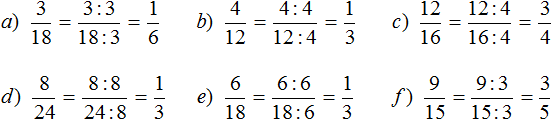







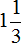


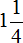
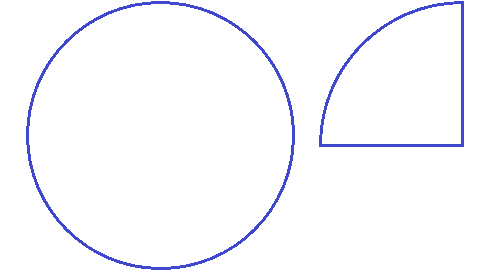
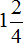
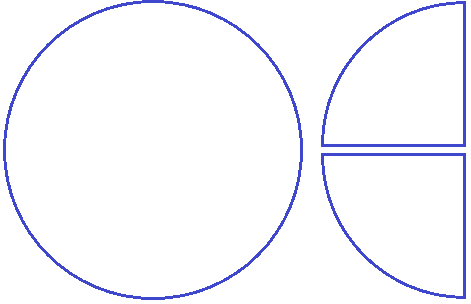
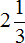


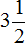

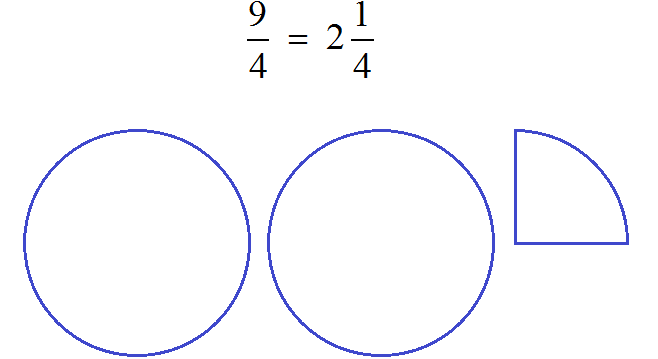

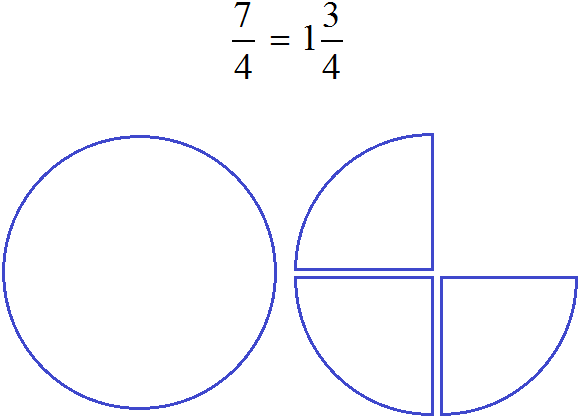

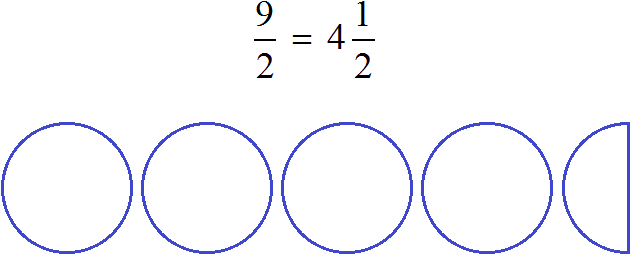

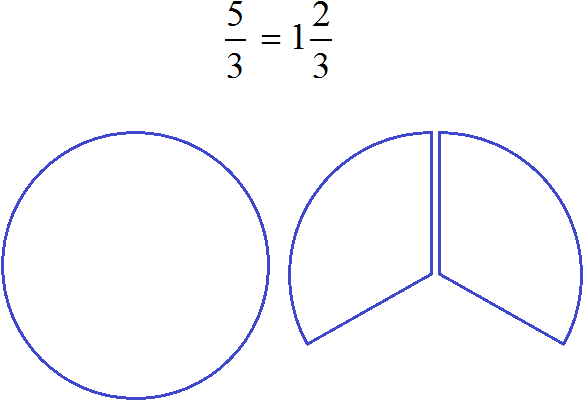
Объяснения очень хорошие. Хотелось бы новых, более сложных уроков в таком же виде.
Здравствуйте. Я бы не назвал это «Началом изучения» именного алгебры, а «началом изучения математики» Думал, что здесь будут темы сначала 7-8 классов (так как именно с этих классов начинается именно алгебра) А так, авторы молодцы, хорошо постарались для тех, кто вообще не знает математику 😉
Спасибо вам большое!Вы мне очень помогли,вы хорошие люди
Вчера спросила про простые числа. Нашла ответ на вопрос в теме Шаг 11. Делители и кратные
Здравствуйте! В последнем примере данной темы указано, что надо сократить дробь 20/40 способом разложения на простые множители. Фактически решается пример на сокращение дроби 32/36. А в общем все очень доходчиво и понятно. Будем повторять с ученицей 4 класса с самого начала. Спасибо за материал.
Круто, выручили, теперь смогу научить ребенка, круто что с рисунками и все разжовано еле нашла такое подробное разъяснение благослави вас бог!!!
Спасибо за такой прекрасный сайт. Только хотелось бы побольше про правильные дроби узнать и примеров побольше, а то только 5/2 и все(((
Здравствуйте, помогите решить сложение дробей 5/23+4/5, дело в том что я не могу найти НОД знаменателей этих дробей (чисел 23 и 5).
Простите, я по ошибке написал. Для решения надо найти НОК этих чисел. Просто я не могу найти НОД у чисел 23 и 5, админ помогите.
Числа 23 и 5 являются простыми. Они делятся только на единицу и самих себя. Поэтому единственным общим делителем для них будет единица.
А НОК для {23 и 5} это 115
Спасибо. У меня еще осталось один вопрос, когда я сокращаю дробь 20/40 вторым способом, при вычеркивании одинаковых множителей, в числителе ничего не остается, а в знаменателе остается толко 2. Вторым способом это дробь, не сокращается что ли?
1/2
нет 20:20=1 получается дробь 1/2
Я правильно понял,что запись 5/2 можно понимать и как
пять делить на два и как пять вторых?
Найдите значение выражения 15/2*5/4-3/8
Проверьте свое решение. Я разве не верно решил?! Если честно, не знаю, откуда был взят этот пример, увидел в ваших комментариях.
15/2×5/4-3/8=15×4+5×2/8-3/8=60+10/8-3/8=70/8-3/8=67/8= 8 и 3/8
Здравствуйте. Спасибо большое за уроки. У меня вопрос. В первом задании разве не будет 1/4 то есть один кусочек съеденного из 4? И в задании четвёртом разве не будет 1/3 то есть один кусочек съеден из 3?
Здравствуйте.
В задании не стоит вопрос сколько кусочков съедено. Нужно описáть рисунок с помощью дроби.
Если перевести на простой язык, то нужно ответить сколько кусочков осталось.
Как перевести 3/4 в 1/4? Ty
Спасибо давно искал подобное с удовольствием обучаюсь успехов вам
Вот! Все ясно,понятно и доступно , намного лучше чем в школе было! Спасибо за старания !
Всё очень понятно, я очень рада что есть ваш сайт т.к. Я не учила математику в школе все 9 классов даже и не думала что математика так интересна) спасибо создателю сайта, и хочется спросить а будут ли ещё уроки? Не именно по этой теме а вообще. Просто хочется до самого 11 класса все понять) и ещё раз вас БЛАГОДАРЮ и желаю успехов в создании уроков!
Спасибо Вам огромное, благодаря таким урокам появился интерес к этому предмету!!!
Спасибо огромное! Такие молодцы! Класс! Все объяснили на доступном языке. А геометрии нету? Чтоб так же понятно было. Или может посоветуете какой-то сайт.
Спасибо Большое!!!!
У вас замечательный сайт и понятное объяснение. Вообще изучение дробей довольно сложно к пониманию с самого начала. И именно наглядный материал помогает ребятам преодолеть этот барьер.
ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ!!!
Летом килограмм клубники стоит 60 рублей. Маша купила 2 кг 500г клубники. Сколько рублей сдачи она должна была получить с 200 рублей?
Ответ:50р сдача
Т.к половина кило это 500г т.е и половина суммы (60р)
1)60:2=30 (р) 500г
2)60+60=120 (т.к она купила 2кг) (р)2кг
3)120+30=150(р)всего
4)200-150=50(р)
Доброго времени суток.
Если вам не составит особого труда, могли бы вы оставлять побольше заданий на самостоятельную работу. Я заметил, что в некоторых уроках задания есть, а в некоторых (как мне кажется важных) вообще нет.
И конечно же, огромное спасибо за данный ресурс. Желаю вам стремительного развития, успехов и заказчиков рекламы побогаче)
Ни как не могу вообразить неправильную дробь в пиццах.
7/3 это одна седьмая часть 3-х?
Представите пожалуйста её наглядно.
Андрей, чтобы вообразить неправильную дробь в пиццах, сначала выделите в ней целую часть. У вас получится две целых и одна третья. То есть две целые и треть, если речь идет о пиццах.
Изучите этот урок. Он идет в дополнение к данному.
Задания с графикой дают четкий смысл дробей. Спасибо за урок!
Спасибо, теперь ясно. Посмотрю дополнение.
разделите пожалуйста девять яблок на пять человек
Сначала каждому раздаётся по одному целому яблоку. Останется еще четыре яблока. Далее каждое из оставшихся четырех яблок разрезают на пять равных частей и раздают эти части поровну. В итоге каждому достанется по одному целому яблоку и по четыре дольки из пяти.
Спасибо за ответ. Смешанная дробь это и показывает. Четыре дольки остаются, значит их никто не получит, т. е. без остатка не обойтись?
Супер. Отличная работа!
Учить учить и учить!!!
только не всегда учить а то измучиешься
20
или
9. 4
— = 1 —
5. 5
Извините, поспешил с вопросом. От каждого яблока одна оставшаяся долька достается пятому человеку.
Вернее, от четырех яблок
ну как можно от Четырех яблок отнять 5 или 6 или от читырех отнять 3 будет 2 это просто что отнять это как умножения
Спасибо за прекрасный урок.Все ясно 🙂
может бывает что этот урок может быть очень сложным потому что Математика С нуля это очень сложно хотя не так уж сложно шучу
Спасибо за доступные объяснения! С пиццами вообще все становится понятно. Буду ждать следующих тем. Спасибо!)))
Админ спасибо тебе за твой труд,можеш гордиться собой смотри сколько людей помог изучать математику заново..!
В задании 8 под буквой d нет ответа
И укажите как читается выражение 1 целая 3/5 , пришлось в интернете искать спасибо
Супер
Плохо понимаю дроби. Пропускаю и не успеваю по математике. Решила с начала учить все точно и чотко по дробям, в итоге нашла ваш сайт. Очень полезный сайт, как мне кажется. Удобный и понятный. Благодарю автора, за проделанную работу.
P.S я больше гуманитарий, но ваш проект даёт мне все доступно понять.
В примере где сокращаются дроби девять двадцать седьмых , там ведь НОД = 9 разве нет? Почему делим на 3 то?
Откройте пожалуйста счёт чтобы можно было в качестве благодарности за ваш труд перевести финансы на развитие проекта
Большое спасибо, Рустам. Не стоит.
Большое спасибо вам за этот проект, успехов !!!
Спасибо и Вам
помогаю деткам своим домашку делать по Вашим материалам.заодно все , чего недопоняла сама (много лет назад) в школе — усваиваю тут.спасибо!!!!
Молодцы! И Вам спасибо!
Спасибо вам огромное за этот сайт ❤️
Пожалуйста 😉
Ошибка нумерации: после восемнадцатого номера сразу двадцатый идёт.
Спасибо, обязательно вставим.
Любо я попутал, либо вы так вставили, но теперь после семнадцатого сразу девятнадцатый.
Пока ещё ничего не трогали) Руки не доходят)
Задание 7, вариант второй.
18/9.
При делении остатка и правда не осталось. Есть целая часть — два. В ответе так и оставили. Только цифру два. А знаменатель 9 куда дели? Его можно убирать?
При выделении целой части в дроби 18/9, получается 2 целых. Дробных частей не остаётся.
Спасибо Вам!
А дробную часть в смешанном числе можно сокращать?
Н-р, 9 3/6 = 9 1/2
Либо только саму неправильную дробь?
57/6 = 19/2 = 9 1/2
И вам.
Да, можно.
Ну да это Клева
Я хоть математику в школе на 4 тянул, но очень многое забыл, а вот уже как 7 месяцев увлёкся программированием и тут то наткнувшись на бинарные коды и пришлось обращаться к математике снова. Спасибо за вашу работу, очень помогает освежить память и узнать что-то новое.
Такого НОД для дроби 23/5 нет
Т.к 23 не делится на 5
Из данной дроби можно выделить только целую часть.
23 делим на 5 = получаем 4 целых и 3/5 = все равно что 5/5 берем по четыре раза, т.е 5/5 +5/5 + 5/5 + 5/5 + 3/5 = 23/5
Кнопка «Показать решение» не работает, исправьте пожалуйста.
Большое спасибо людям которые являются авторами курса «Математика с нуля». Для меня математика очень страшный предмет был изначально но с помощью этого сайта у меня страх прошел:).
-Было бы круто если бы нашел такой же сайт или книгу по качеству объяснения — об математических методов исследования операций и криптографии.
-Успехов Вам!
Спасибо Вам!
Я не понял как мы в случае сокращения 3 зачеркнули и вместо нее 1 поставили.
Разделили эту тройку на 3. А три разделить на три будет 1
Здравствуйте! «Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя» — тут действительно должен быть союз И? Просто с И получается, что если в дроби (одновременно и в числителе, и в знаменателе) стоит простое число, то сократить её не получится. Может быть, уместнее использовать союз ИЛИ?
ИЛИ не подходит, например, 3/12 это 3 простое, 12 составное, сокращается до 1/4, а когда оба простые, как 3/11 например, не сокращается. Так что действительно союз И.
П.с. Отличная подача материала, я в восторге)
А 3/28 сможете сократить?..
Кстати, если выбирать союз из примера несократимых дробей администратора, то выбрать получится только ИЛИ, потому там есть 3/4.
Так-так, я был невнимателен. В вашем примере знаменателем является натуральное, или составное, число. К нему союз И не подходит.
Ой, ещё раз невнимателен…
ну в пол 2 ночи сидеть за интернетом это как то очень поздно в это время спят а ни сидят за комьютером вы помойму не выспались сидите по ночам за интернетом глазкам тоже нужет отдых а то глаза упадут на клавитуру и все
Добрый день,тема 12(дроби) — Выделение целой части дроби, в последнем примере — 57/6 сказнно что результат будет 9*3/6 . Но разве 57/6 не даст 19/2 который будет 9*1/2?
Ах все,понял
Спасибо за урок! До 5 класса тянул математику на 8 ( 10 бальная система оценок) Но в 5 классе пришел ужасный учитель и он так преподавал, что большинству (включая меня) стало неинтересно. И мы забили. А учитель натягивал отличников , кое-как то помогал, то не помогал среднячкам, и забил на помощь отстающим. Сейчас заканчиваю 10 класс, хоть и большо связал обучения с изучением языков , вдруг захотелось саморазвития в той области которую мне не объяснили и не показали мне всю красоту математики. Спасибо вам за чуть меньше чем 2 недели прошел все ваши 12 ШАГОВ ( изучил НОД, НОК, дроби, которые раньше были как инопланетный язык) . Благодаря вам хочется изучать математику дальше и дальше , ОГРОМНОЕ СПАСИБО!
ПС. Учитель по математике до сих пор у нас преподает, но я к нему отношусь с равнодушием …
ну Дроби это как Математика а самом деле это очень сложная математика это да
ну за пятый Клаас это сложно а вот за 6 еще сложнее потом пойдет 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 а потом насамом деле еще сложнеее
ну в это время не кто решает такую Матетиматику в это время спать надо а ни матиматикой заниматься
а ни кто математикой не занимается люди просто в это время спят ну многие делают эгзамен но не ночью это можно и днем
Спасибо за проделанную работу, Вы лучшие! Сама поняла и могу толково объяснить ребенку четверокласснику.
Благополучия и процветания Вам! Сайт драгоценный!
Настолько сложная тема и длинная статья, что даже почти на месяц приостановил изучение, слишком много было дел, хотя всегда Ваш сайт на вкладке открыт. Всё таки до конца дошёл темы и решил задачи.
Благодарю Вас от души, так доходчиво и понятно мало кто объяснит, такие не очень лёгкие темы.
Ваш сайт нужно рекомендовать всем, что я и буду делать.
Для меня тема НОД и НОК оказалась сложней чем дроби! (((Просто видимо не надо торопиться!
В больнице делать нечего, благодаря вашему сайту хоть с дробями подразобрался. Спасибо!
Очень интересная и полезная статья.
Хорошая работа
Мне обидно так…
Я давно пользуюсь Вашей работой, слежу за пополнением Шагов, сам начал с нуля… Вот сегодня, например, столкнулся с проблемой понимания «обратной дроби», остановился на заголовке, перечитывал не большой отрывок снова и снова, полез в инет, дяде Гуглу, в Ютуб, пересмотрел кучу блогеров и инетуроков, где все говорят одно и тоже, будто сговорились и с одного листочка читаю и пришлось вернуться на сайт, расстроенным… Я не понял смысла обратной дроби: как 5 пицц становятса одной пиццой?! Зачем переварачивать дроби?! и все в стаком духе.
Но, прокрутил отрывок чуть вниз и ИМЕННО ТУТ все стало ясно как в ясный день!
Мне так обидно!
В день, когда я обнаружил, что вы добавили «поддержку» я сам нахожусь немного в беде… Но, ничего! Я обязательно Вас поддержу!
Благодарю Вас за такой труд, назвать «большой» или «титанический», корого, — ничего не сказать
Спасибо и Вам. Желаем успехов в обучении.
Воу спасибо ща помощь
Благодаря вашим урокам я научился рисовать. Благодарю от всего сердца
Здравствуйте, помогите пожалуйста, тему я понял. Но вот самостоятельные задания как то не понимаю, ну точнее говоря понял, но вот в чем проблема, начиная с задания 26. Изобразите в виде рисунка следующую дробь: . Я все задания понял как делать, но пытаюсь самостоятельно для себя придумать и решить не получается, пытаюсь изобразить в виде рисунка дробь 8/3 но не получается, можете сказать что не так?
Выделяем целую часть дроби 8/3. Для этого можно посчитать в уголке. 8:3=2 и 2 остатке. Значит, в целую часть идет 2, в числитель 2 и в знаменатель 3 — получается 2 2/3. А это значит, рисуем 2 целых пиццы и рядом 2 из 3 кусочков отдельно. Поправьте меня, если я неправильно объяснила, сама сейчас все изучаю с нуля. Всем удачи!
Здравствуйте, я понял тему но как только стал задание самостоятельное делать(сам себе придумывал) например решил сам сделать 8/3 в виде рисунка но не смог, почему не получается не понимаю)) можете помочь или показать?
8 делим на 3, в итоге получаем целую 2, в числителе 2, а в знаменателе 3, представив в виде рисунка получаем, 2 целых круга, и 2 кусочка от круга разделённого на 3, надесю более менее объяснил
Класс ☺
Очень внятно
Дробь не правильная, нужно перевести в смешанную дробь,получить целое с остаткам и потом рисуй себе на здоровье.
8/3=2цел. 2/3
«Если в числителе И знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается.»
А почему дробь 3|4 несократима ?
Число 4 ведь не являеться простым числом.
потому что 3 – простое число.
Здраствуйте!
Почему НОД у 20 и 40 = 20, если правильно 10?
20=2*2*5 и 40=2*2*2*5 и тогда НОД = 2*5=10
нормально, только как 1 можно поделить на 3?
Главный вопрос не решён.
2*2*5=20
здравствуйте, в заданиях 14-15, не написано на сколько нужно сократить дроби. откуда можно узнать какое число взять? чтобы сокртотить. заранее спасибо
это очень круто, спасибо за такой подробный урок !!
вы замечательные люди !! спасибо
спасибо вам огромное!! нахожусь в 7 классе, но до сих пор плаваю в некоторых темах. Всё разборчиво, понятно, просто изумительно. Спасибо правда, многое уже что разобрала и поняла
Скажите пожалпожалуйста,в одной упаковке 5 ампул нужно списать 2 аипулы с упаковки. Помогите пожалуйста
Интересно, почему в школе не обучают таким наглядным образом как на данном сайте? Даже не пытаются объяснить что из себя представляет дробь, сразу учат выполнять действия с дробями не объясняя наглядно для чего они вообще нужны и что из себя представляют. Наверное учителя в школе и сами не особо разбирались, как в школе научили так и рассказывают. Впервые в жизни осознал образ дроби у себя в голове благодаря данному сайту. Спасибо огромное автору.
Большое спасибо за ваши труды!
Норм тема.
Идём дальше.
спасибо за этот урок. очень интерестно изучать когда вы так подробно объяснили.
Здравствуйте, благодарю вас за вашу работу, единственный сайт благодаря которому я начал разбираться в математике!
Теперь мой вопрос таков, я не понял момент с несократимыми дробями, там вы привели примеры что если в знаменателе и числителе есть простые числа, эта дробь несократимая, но тогда почему вы сократили дробь 9
27. Ведь число 9 это простое число, поэтому дробь должна быть несократимой? Объясните пожалуйста этот момент, спасибо большое!
Добрый день. Спасибо и Вам.
Число 9 составное. Оно имеет более двух делителей. Оно делится на 9, на 3 и на 1
Все понял, выполнил все задания, спасибо большое, идём дальше.
А есть ещё такой же сайт как этот но только по физике?
ААААА ЭТИ ДРОБИ НЕЕЕТТТТТТ АААААААААААААААААААА
МАТЬ МОЯ ЖЕНЩИНА АААААА .
К сожалению нет