Если в квадратном уравнении ax2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D1 = k2 − ac, а корни по формулам  и
и  .
.
Примеры
Решим квадратное уравнение x2 + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.
Любое четное число n можно представить в виде произведения числа 2 и числа k, то есть 2k.
n = 2k
Например, число 10 можно представить как 2 × 5.
10 = 2 × 5
В этом произведении k = 5.
Число 12 можно представить как 2 × 6.
12 = 2 × 6
В этом произведении k = 6.
Число −14 можно представить как 2 × (−7)
В этом произведении k = −7.
Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.
В уравнении x2 + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.
Найдем дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = 32 − 1 × (−16) = 9 + 16 = 25
Теперь вычислим корни по формулам:  и
и  .
.
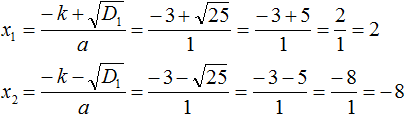
Значит корнями уравнения x2 + 6x − 16 = 0 являются числа 2 и −8.
В отличие от стандартной формулы для вычисления дискриминанта (D=b2 − 4ac), в формуле D1 = k2 − ac не нужно выполнять умножение числа 4 на ac.
И в отличие от формул  и
и  формулы
формулы  и
и  не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.
не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.
Пример 2. Решить квадратное уравнение 5x2 − 6x + 1=0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = (−3)2 − 5 × 1 = 9 − 5 = 4
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами  и
и 
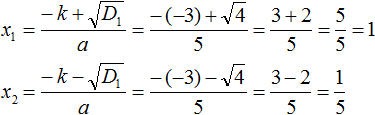
Пример 3. Решить квадратное уравнение x2 − 10x − 24 = 0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = (−5)2 − 1 × (−24) = 25 + 24 = 49
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами  и
и 
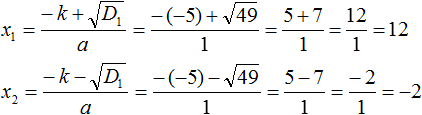
Обычно для определения числа k поступают так: делят второй коэффициент на 2.
Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2
![]()
Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2
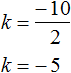
Пример 5. Решить квадратное уравнение ![]()
Коэффициент b равен ![]() . Это выражение состоит из множителя 2 и выражения
. Это выражение состоит из множителя 2 и выражения ![]() . То есть оно уже представлено в виде 2k. Получается, что
. То есть оно уже представлено в виде 2k. Получается, что ![]()
Найдём дискриминант по формуле D1 = k2 − ac
![]()
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами  и
и 
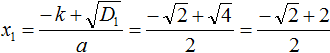
При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.
В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен 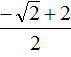 .
.
Вычислим второй корень уравнения:
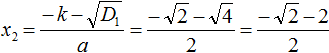
Вывод формул
Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.
Рассмотрим квадратное уравнение ax2 + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k
b = 2k
Заменим в уравнении ax2 + bx + c = 0 коэффициент b на выражение 2k
ax2 + 2kx + c = 0
Теперь вычислим дискриминант по ранее известной формуле:
D = b2 − 4ac = (2k)2 − 4ac = 4k2 − 4ac
Вынесем в получившемся выражении за скобки общий множитель 4
D = b2 − 4ac = (2k)2 − 4ac = 4k2 − 4ac = 4(k2 − ac)
Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k2 − ac.
В выражении 4(k2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k2 − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.
То есть выражение k2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D1
D1 = k2 − ac
Теперь посмотрим как выводятся формулы  и
и  .
.
В нашем уравнении ax2 + bx + c = 0 коэффициент b заменён на выражение 2k. Воспользуемся стандартными формулами для вычисления корней. То есть формулами  и
и  . Только вместо b будем подставлять 2k. Также на забываем, что D у нас равно выражению 4(k2 − ac)
. Только вместо b будем подставлять 2k. Также на забываем, что D у нас равно выражению 4(k2 − ac)
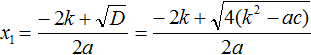
Но ранее было сказано, что выражение k2 − ac обозначается через D1. Тогда в наших преобразованиях следует сделать и эту замену:
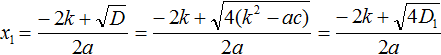
Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:
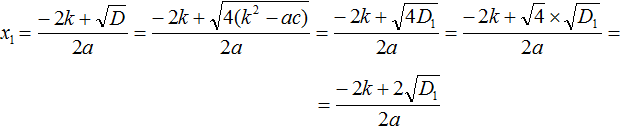
Теперь в получившемся выражении вынесем за скобки общий множитель 2
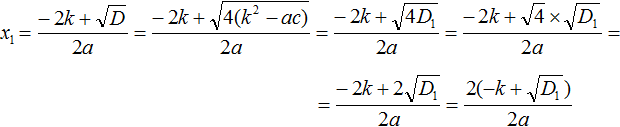
Сократим получившуюся дробь на 2
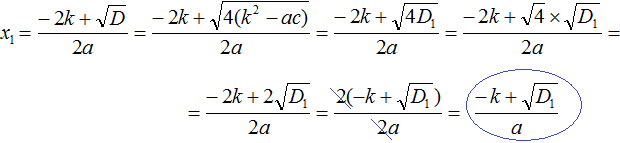
Аналогично вывóдится формула для вычисления второго корня:
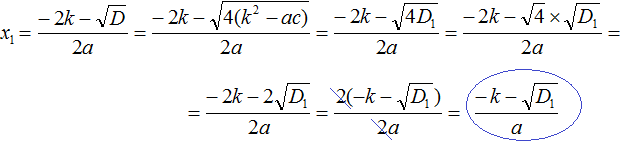
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
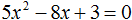
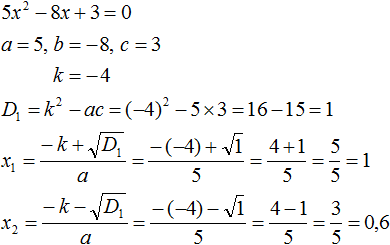
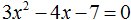
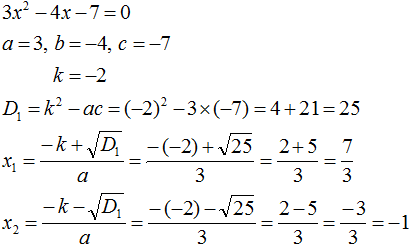
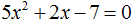
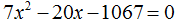
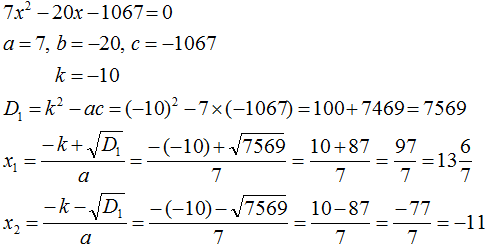
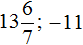
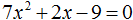
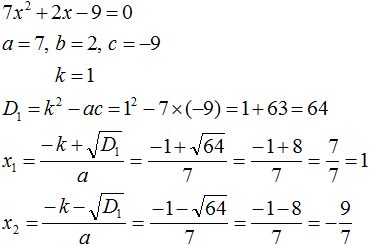
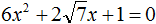
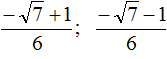
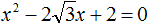
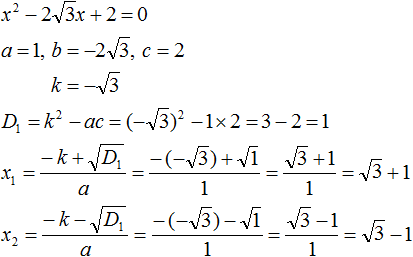
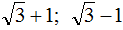
Спасибо за уроки, по возможности задоначу, очень доходчиво
Доброго времени суток Администратор, надеюсь эта тема, не последняя.
5. Пример. Подскажите пожалуйста почему ответ
-√2+2
÷2
для выражения 2(x^2)+2√2x-1=0
такой? Если ответ подставить то получается
0,171572874+0,828427122-1=но не 0
Даже не приблизительно
Очень крутой сайт, с помощю вашего ресурса подтянула математику, продолжайте в том же духе!
Самый крутой сайт с объеснениями. Спасибо!!
very cool
С большим удовольствием села опять перед квадратными уравлениями. В школе не проходила- я кончила школу в 1958г. Алгебру знала хорошо- отец был математиком. Квадратными у уравнениями столкнулась. когда надо было объяснять внучке. Тогда у меня были двойные проблемы. Надо было самой понять решения квадратных уравнений и это объянить внучке на французском языке. Пришлось сесть капитально. На днях попались ваши уроки. И снова я села за квадратные уравнения. Порешала полные . неполные уровнения и оказывантся есть ещё и с чётным вторым коэфициентом- не знала , что они решаются по особому,
Мне 83года, Пенсионерка. Учу детей французскому языку- это моё хобби. Спасибо, учу свой мозг не забывать…