Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
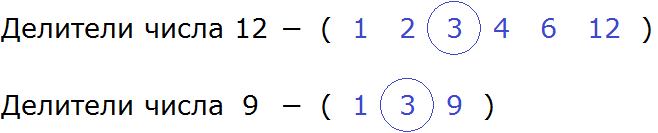
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: 
и 
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
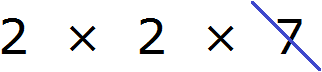
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
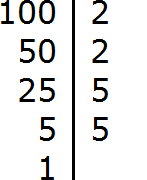
Раскладываем на множители число 40
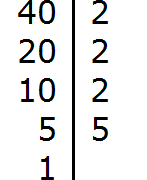
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
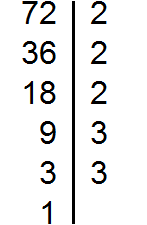
Раскладываем на множители число 128
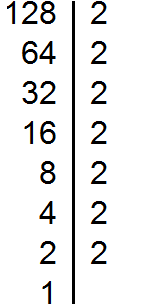Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
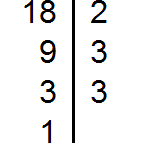
Разложим на множители число 24
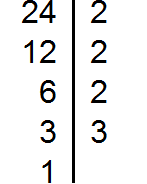
Разложим на множители число 36
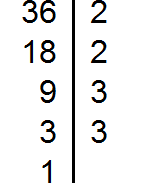
Получили три разложения:
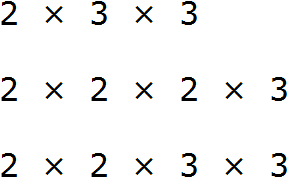
Теперь найдём и подчеркнём общие множители:
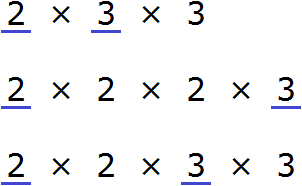
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
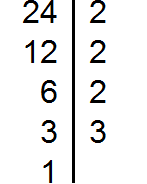
Разложим на множители число 36
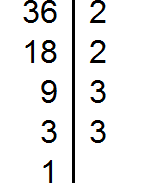
Разложим на множители число 42
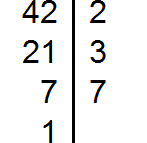
Получили четыре разложения:
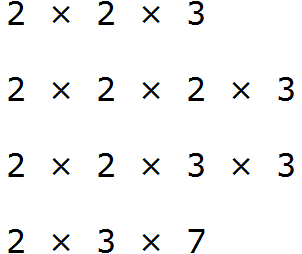
Теперь найдём и подчеркнём общие множители:
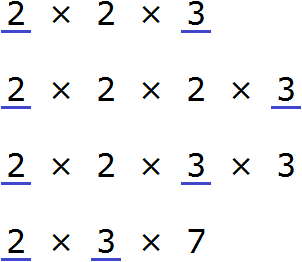
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
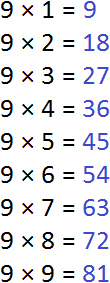
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
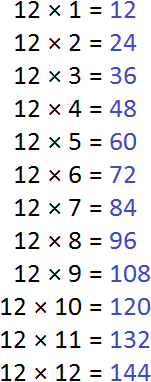
Теперь выпишем кратные обоих чисел:
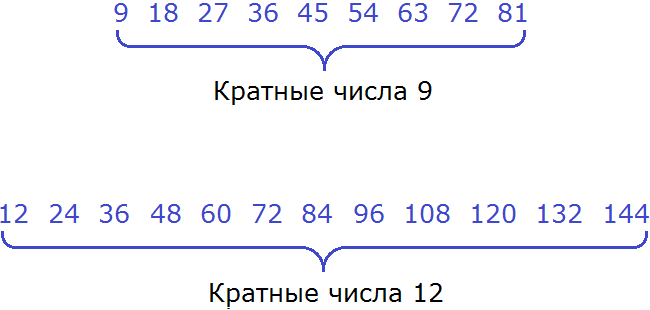
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
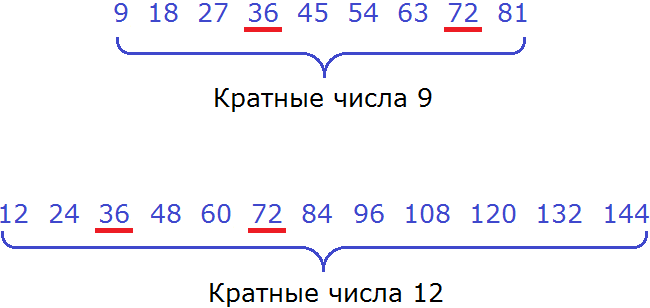
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Разложим на множители число 9
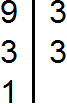
Разложим на множители число 12
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
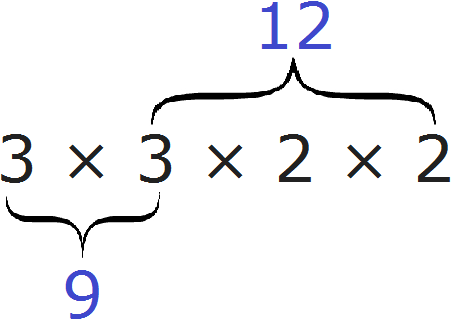
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
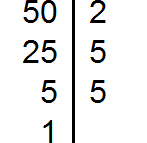
Разложим на множители число 180
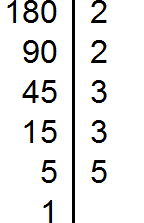
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
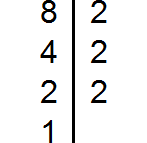
Разложим на множители число 15
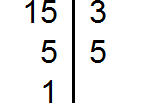
Разложим на множители число 33
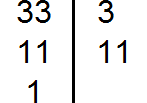
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
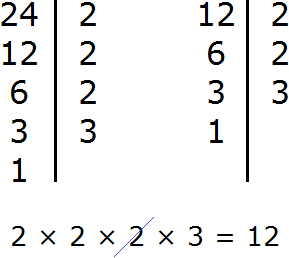
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
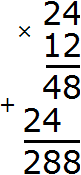
Разделим полученное число 288 на НОД чисел 24 и 12
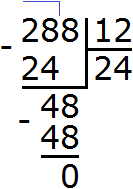
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
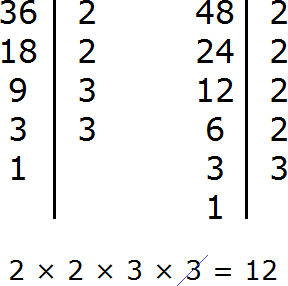
Перемножим числа 36 и 48
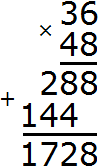
Разделим 1728 на НОД чисел 36 и 48
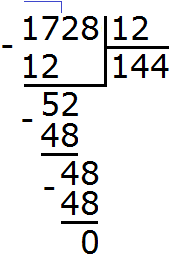
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
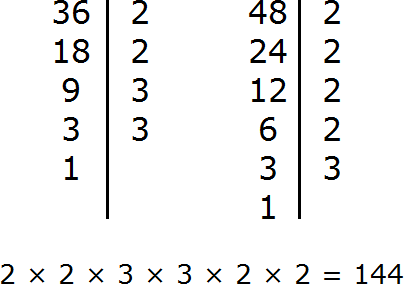
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
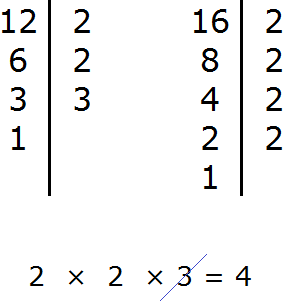
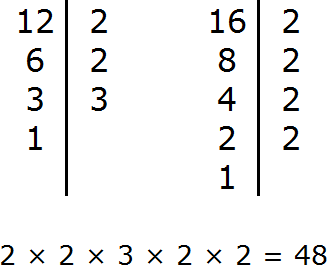
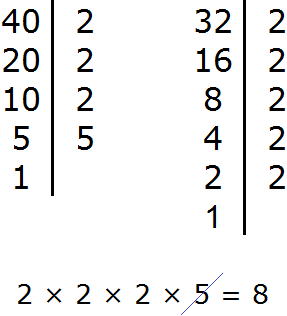
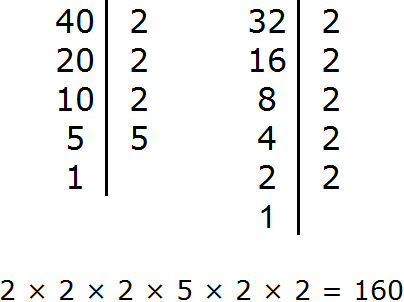
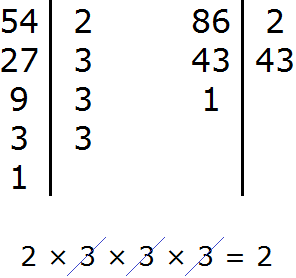
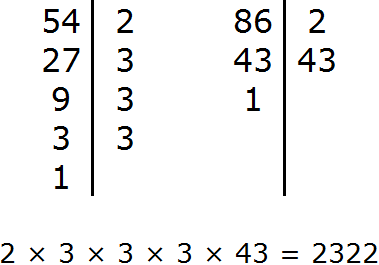
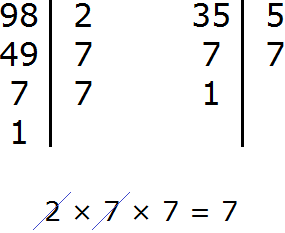
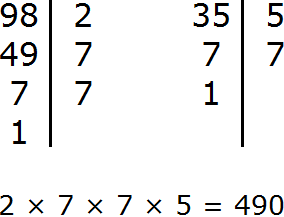
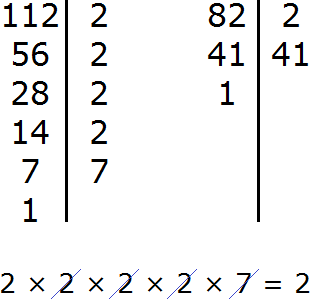
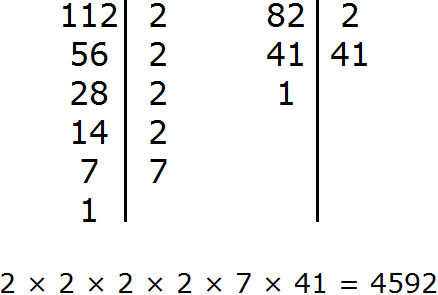
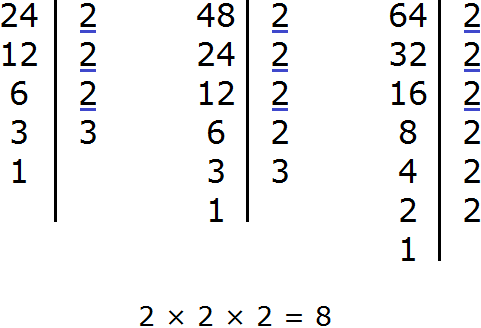
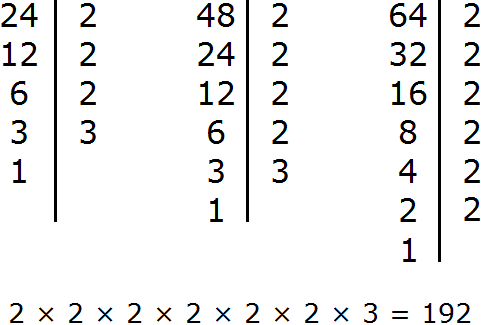
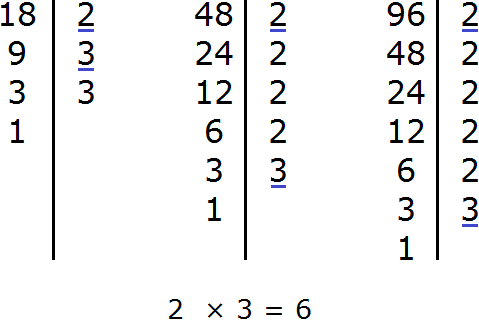
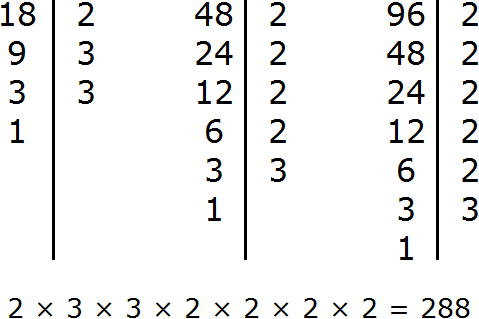
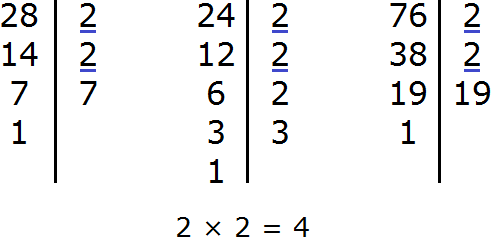
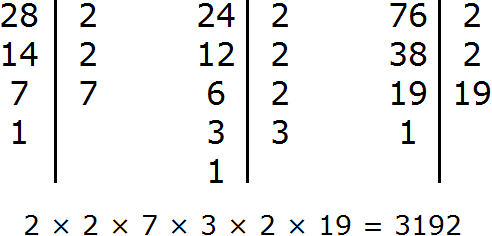
А по какому критерию определять, какое число является первым, а какое вторым?
без разницы. По желанию. Первое можно принять за второе. А второе за первое. В обоих случаях ответ будет одинаковым
Второй способ нахождения НОД у меня не получается, если числа поменять местами. Например первое число 28 второе 42. Для 28 множители (2*2*7) для 42(2*3*7) какие числа вычеркивать?
Всё правильно. Из разложения первого числа 28 вычеркни одну двойку, т.к. её нет во втором разложении (там только одна 2).
Останется 2*7. Перемножаешь 2 и 7 — получаешь 14. И это будет НОД для {28 и 42}
Спасибо!!! теперь дошло:) 🙂
Спасибо. Я тоже не сразу понял как определить первое и как именно вычеркивать того чего нет..)
P.S. Ошибка была в том что я думал, если есть хоть одна похожая цифра надо оставлять все такие же цифры первого числа. А оказывается надо вычеркнуть столько сколько там лишних, по мимо тех которых нет.
здравствуйте, всё прекрасно.
но когда я начинаю писать задания, например нужно найти НОК чисел 28,24,76.
в таких случаях я начинаю не понимать.
почему там внезапно появляется 2 ?
А с тройкой что стало?
НОД 14 НАДО ВЫЧЕРКНУТЬ 2И 3
Ищите совпадения. Совпадений два. Числа 2 и 7 повторяются в обоих случаях по два раза. Их и перемножайте. Получится 14. Это и есть наибольший общий целитель.
Второй способ это найти общие множители. А то что Editor описал это 3й способ с вычёркиванием. P.s небольшая поправка
Если взять, как у вас , первым числом 28, а вторым 42, то из ряда по разложнию первого числа (2*2*7) нужно вычеркнуть лишнюю двойку , ведь ее нет во втором числе, а затем умножить оставшиеся 2*7=14 — это НОД (28,42).Если же взять наоборот первым 42, а вторым 28 то из раскладах первого числа (2*3*7), нужно вычеркнуть 3, т.к. его нет в раскладе второго числа). Останется 2 и 7. Перемножаем = 14. Тот же результат : НОД(42,28) =14.
Не совсем понятно но спасибо за ваш труд потому что тема реально сложная!
Я вот что не понял, как все таки определить какие простые множители исключить, а какие оставить и перемножить
Без разницы , можно любое число в начале и конце
Там сказано что надо найти НОД чисел периметру 12 и 6 значки 12 первое число)
А по моему, данная тема лёгкая, и не нудная так то=) очень даже весело.
согласна
Хороший сайт, дружественный.
Сайт отличный я из Узбекистана
спасибо очень помогли а то я не как не мог понять эту тему 🙂
Капетссс узбеееек хахаахахахх
Спасибо большое вам за такой труд, буду ждать с нетерпением продолжение ,
Скажите пожалуйста , а как будет НОД , 1512/2,1980/2,3276/2
И вообще можно сразу 3 примера решать сразу ??? И объясните пожалуйста в краце как будет если вместе НОДа будет НОК ?? Спасибо заранее!!
Мухаммад, не совсем понятен вопрос. Вы ищете НОД от дробей или что это у вас? Сразу найти НОД от нескольких чисел можно, для этого нужно разложить на простые множители эти числа и найти произведение общих простых множителей этих чисел.
Подскажите пожалуйста НОК (40 и 32) = 8 или 160
160
Спасибо большое , я все уже понял!!! Извините за некоректный вопрос!!!
А, для чего это??
Админ, скажите, правильно ли я выяснил, что НОД и НОК для нечётных чисел получить нельзя?
НОД и НОК можно находить для любых чисел. Нечётные числа тоже ведь можно разложить на простые множители.
Но иногда могут попасться нечётные числа, которые являются простыми числами. В этом случае нод для них будет единицей (поскольку простое число раскладывается только на единицу и само себя), а нок — произведением этих нечетных чисел
Скажите пожалуйста я правильно понял, НОД для 80 и 20 будет 20?
Да, правильно, 20
Я понила и решила это лехкода будет 20
та что лехкода просто я б сказал hard — кода
80 -2 20-2
40-2 10-2
20-2 5-5
10-2 1
5-5
1
2*2*2*2*5 удалить пару двоек?
2*2*5 —
Да, вычеркнуть из первого разложения две двойки)
Спасибо, что поправили. Я вечером додумался самостоятельно, что НОД нечётных чисел будет единица. А вот вчера же искал НОК для чисел 12, 16 и 128. Здесь находятся аж два НОК. Для чисел 12 и 16 это 48, а для 16 и 128 аж 256. Или некорректно искать наименьшие общие кратные для разно разрядовых многозначных чисел? Кстати 128 пришло на ум само собой, и я не ожидал, что что это произведение 16*8.
Наименьшее общее кратное можно находить для любого количества чисел, независимо от того из скольких разрядов они состоят. В вашем случае НОК для чисел 12, 16 и 128 будет число 384
Наименьшее общее кратное для чисел 16 и 128 является число 128. Потому что 128 : 128 будет 1, а 128 : 16 будет 8.
Добрый день, третий способ для нахождения НОК, подходит только для трех чисел?
Если да, сделайте пометку. Поскольку если нужно найти НОД и НОК, одновременно трех чисел, этот способ будет являться ошибочным
Подскажите пожалуйста число НОД для чисел 21 и 704
НОД для 21 и 704 это единица
извените, а как это ? я разложил, и просто не мог найти общего числа, так как единица вышла ?
извените, а как это ? я разложил, и просто не мог найти общего числа, так как единица вышла ?
21 и 704 раскладваем на множители:
21:3=7
7:7=1
704:2=352:2=176:2=88:2=44:2=22:2=11:11=1
Это все делается в столбик.
Теперь со второго столбика вычеркиваем то,чего нет в первом
3,7 — вычеркиваем. Получается 1
Ибо 0 быть не может.
Это если я все правильно поняла
Найдите пожалуйста НОД чисел 50,75,325
НОД (50, 75, 325) = 25
Нок для 50,75,325 :1950?
да
Здравствуйте. Почему Вы сказали, что «Затем, выписываются множители входящие в первое разложение, и добавляют _____недостающие множители_____ из второго разложения», но в примере сказали, что «В первом разложении нет _____двух двоек_____. Их и допишем:». Две двойки это же выражение получается, а не, как Вы сказали выше, множители?
Здравствуйте.
Две двойки из второго разложения нужны для того, чтобы организовать новое разложение куда одновременно входят множители обоих чисел
«Две двойки это же выражение получается, а не, как Вы сказали выше, множители?»
Верно. В итоге получается выражение, состоящее из нескольких множителей, которые нужно перемножить, чтобы получить НОК
Благодарю за Вашу работу, но чего-то не понимаю. Не могу найти НОД 144 и 250.
НОД для чисел 144 и 250 это 2
А мне еще интересно это тема полностью разобрана или нет? Для таких чисел которые без остатка не делятся на 2,3,5,9…..
Здравствуйте!
Помогите решить эту задачу подалуйстa:
Установите соответствие. a и b натуральные числа, c — произведение необщих простых множителей.
1. НОК (a;b)=ab НОД(a;b)=1
2. НОК (a;b)=540 НОД (a;b)=6
3. НОК (a;b)=192 НОД (a;b)=16
а) a и b взоимно простые числа
б) с=6.
в) ab =1734.
г) ab=635.
д) ab =635.
е) с=15
уважаемый админ,я не поняла,почему мы при разложении числа 180,разделили 45на 5 , а не на3? я думала,что делить нужно на наименьшее число
с уважением
Да, вы правильно думаете. Редактор поспешил, разделив на 5. Но на самом деле разницы никакой. Оба расклада верные. Более того, это число можно разложить и другим образом:
Во всех случаях получаются одни и те же множители. С привыканием вовсе перестаёшь обращать внимание на то, как раскладываешь. Главное понять технику.
Но всё же удобнее начать с малых множителей как сделали вы. Это позволяет получить множители, которые упорядочены по возрастанию..
Спасибо!
Круто)
Админ, а для чего в будущем НОДы и НОКи понадобятся.
А то кажется что от делать нечего находят.
Чтобы уметь складывать и вычитать дроби, сокращать их. Есть также немало задач в которых ищется НОД и НОК
когда использовать нод а когда нок при ришении выражений, есть ли какоето правила определяющее отдельные случаи их приминения?
зависит от задачи, которую вы решаете. Например, если вы хотите сократить дробь, то нужно использовать НОД. Если ищете общий знаменатель дробей, то используете НОК.
Существуют также задачи, которые необходимо проанализировать, прежде чем решать их. Потому как только после анализа становится ясно, что использовать НОД или НОК.
Подскажите пожалуйста, НОК 360,245 и 18. Решала с интернета. Разложила на множители 360(22255) и НОК получился 29400,проверила ответ, оказалось неправильно. Разложила 360 по другому(223325)получилось совсем другое 17640, этот ответ засчитали верным. Не понимаю в чем ошибка, читала выше что разницы нет.
В разложении числа 360 ошибочка — не хватает двух троек и одна пятерка лишняя. Должно быть либо 222335 либо 222533 либо то, которое вы получили позже
Или как-то так:
>> Не понимаю в чем ошибка, читала выше что разницы нет.
Да, разницы нету. Посмотрите как в этот раз разложилось число 360, но НОК не изменился:
Ваше последнее разложение тоже кстати верное
Спасибо
может правильно будет 2520?
360 2 245 5 18 2
180 2 49 7 9 3
90 2 7 7 3 3
45 3 1 1
15 3
5 5
1
2*2*2*3*3*5*7=2520
Можно и так разложить, но в итоговом перемножении множителей нужно дописать еще одну семерку:
2*2*2*3*3*5*7*7=17640
__
С \(А∩В)
P=2
Q=3
R=5
Спасибо большое создателям и авторам сайта!Дизайн наипростейший и очень удобный.А днания которые я тут получаю компенсируют все то что я в свое время пропустил!Большое вам спасибо ребята!вы мои кумиры!)
Полностью к Вам присоединяюсь!
Кстати 3ий способ нахождения нок можно сделать по другому.
Сначала найти нок чисел потом перемножить их и затем разделить их произведение на нок. Эта крута
^~^
Спасибо! В следующем году ОГЭ за 9 класс. Математику не понимаю, но нужно 4 в аттестате, а то стыдно как то. В 5 классе ужасная учительница была, и эту тему именно тогда и проходили, яечго не поняла на тот момент. Сейчас поняла. Мне кажется нужно включить немного заданий для решеня, потому что тема сложная, много нюансов
Здравствуйте. подскажите почему в задание 16 двойка последняя повторяется?
Вечер добрый! Почему при нахождении НОД мы вычеркиваем числа, котороые не входят в разложения? А при нахождении НОК, наоборот дописываем? Не совсем понятно по какому принципу получаем окончательное общее число. Когда решаю с примером и прям по шагам, которые описаны — понятно, а шаг вправо, шаг влево — теряешься, не понятна до конца работа с полученными разложениями. Поясните, пожалуйста! Или это просто надо запомнить и всё?
Здравствуйте.
Вычеркивают, чтобы остались только те множители, которые являются общими в обоих числах. НОД ведь состоит из произведения общих простых множителей.
А при поиске НОК множители наоборот дописывают, чтобы получить новое разложение, куда входили бы множители обоих чисел.
Как мы находили наибольший общий делитель в школе? Я использовал только один способ, перебирал варианты, проверяя подходит то или иное число, делится ли оно на оба знаменателя в дроби или нет, если делится, то можно ли потом оба знаменателя поделить еще и так далее.
Возьмём конкретный пример. Числа 18 и 24. Начнём с простого, оба числа можно разделить на 2. Получатся числа 9 и 12. Хорошо. 9 и 12 можно разделить на 3. Получатся числа 3 и 4. Все, на этом общие делители закончились. 3 и 4 уже нельзя разделить ни на 2 ни на 3. В итоге мы разделили 18 и 24 сначала на 2 затем 3. Если перемножить 2 и 3 получим 6. Это и есть наибольший общий делитель. Другой пример. 32 и 24. Делим на 2, получаем 16 и 12. Делим еще раз на 2, получаем 8 и 6. Делим еще раз на 2, получаем 4 и 3. Все. В этот раз мы проделали три шага и в каждом делили на 2. Тогда умножаем 2 на 3 шага, получаем 8. Это наибольший общий делитель.
Еше один пример. 32 и 48. Оба числа делим на 2, получаем 16 и 24. Снова делим, на 2, получаем 8 и 12. Снова делим оба числа на 2, получаем 4 и 6. Можно еще раз поделить на 2 и получаем 2 и 3. Все, в итоге мы совершили 4 действия, в которых делителем было число 2. Проделаем следующее, 2 × 2 × 2 × 2, получим 16. Это и есть НОД. Почему именно так? Почему двойки нужно умножать? А не складывать? Ну… главное что это работает;)
В задании где нужно найти НОД, а потом НОК чисел (18, 48, 96), я совсем не понимаю… Откуда там появляются те 2 двойки ? Почему они появляются, если в разложении числа 18 — только одна двойка ? Очень надеюсь что кто-то мне объяснит, так как нахожусь в замешательстве.
Двойки нужны для того, чтобы итоговое разложение включало в себя множители чисел 18, 48, 96.
Разложение 2×3×3×2×2×2×2 и включает в себя множители этих чисел.
Примерно так это можно себе представить
Всё равно не понятно. Откуда взялась эта двойка? Я понимаю что это универсальное разложение, но как до этого додуматься когда в правиле написано «Дописать множители из второго числа, которых нет в первом»?
Ещё вопрос. Если, при нахождении НОД 3х чисел, при разложении у одного остаток. Получается у них нет НОД?
Всё, ответ не нужен! Разобралась
Не понятно как находить НОК для трех чисел
Почему вычеркнули 3 из первого задания, не пойму!! Обьясните
Чтобы получилось произведение общих простых множителей.
Добрый вечер! Не получается решить задачу.
Периоды обращения вокруг Солнца планет Земной группы составляют : Меркурия – 88 суток, Венеры – 225 суток, Земли – 365 суток , Марса 687 суток . Через какой наименьший период времени состоится парад планет , при котором в своем движении по орбитам они оказываются на одной линии?
Ответ должен быть 704 года. Задача из задачника, может я неправильно НОК нашел.
В задании 9, 56/2 будет 23.
Лол, админ в прошлой теме я не мог оставить коментарий, т.к твоя система защиты приняла меня за врага, который посредством sql кода пытался получить доступ к DB.
[spoiler]Этот комент можно не публиковать[/spoiler]
Класс! Жду новых уроков!
Но бывают же числа у которых нет общих делителей или кратных? Что в таких случаях делается?
Как минимум у любых чисел есть общий делитель 1. Тогда вы говорите, что это взаимно-простые числа, не имеющих общих делителей, кроме единицы. Наименьшее общее кратное взаимно-простых чисел a и b это произведение чисел a*b.
А если во втором способе одинаковых совпадающих цифр несколько?
Почему-то не действует третий способ нахождения НОД. Например надо найти НОД 12 и 16.
12|2
6|2
3|3
1|
И
16|2
8|2
4|2
2|2
1|
В первом числе есть число 3, что не во втором числе. Значит вычеркиваем. Остается 2 и 2. Перемнржаем. Получается 4. А правильный ответ 48.
Не путайте НОД с НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
НОД (12; 16) = 4
НОК (12; 16) = 48
Здравствуйте! Скажите пожалуйста в вашем примере где вы раскладывали на множители число 180, получилось вот так: 180:2, 90:2, 45:5, 9:3, 3:3
А у меня получилось так: 180:2, 90:2, 45:3, 15:3, 5:5.
Как правильно? Спасибо заранее!
Здравствуйте.
Оба варианта правильные. В разложении числа 180 есть две двойки, две тройки и одна пятерка
спасибо!!!
Для меня это лучший сайт, и для тех кто только начинает учить математику. Спасибо admin. Если не секрет вы сами где учились?
Добрый день. НОД чисел 24 и 18 вторым и третьим способом, получаются разные числа. Вторым способом 6, третьим способом 4. Разъясните пожалуйста.
Рассмотрены разные примеры:
НОД (24 и 18) = 6
НОД (28 и 16) = 4
Тяжелая тема для освоения с повтором проходил но все таки усвоил, ее надо не спеша проходить, примеры для задания немного числа местами поменяли тем самым запутали, но это кажется к лучшему начинаешь выяснять что тут не правильно — тем самым хорошо усваиваешь тему. Спасибо разработчикам
«Для нахождения наименьшего общего кратного (НОК) можно пользоваться двумя способами»
Здравствуйте , y вас есть два способа, но есть 3 способа , fix it please , sorry , i used only English keyboard…
Здравствуйте! подскажите пожалуйста , откуда здесь в конце тройка
Задание 12. Найдите НОК чисел 24, 48, 64
Решение: 2*2*2*2*2*2*3 ?
Здравствуйте. Чтобы получилось разложение куда входили бы множители каждого из чисел 24, 48, 64.
Посмотрите на разложение 2*2*2*2*2*2*3. В нем есть множители каждого из чисел 24, 48, 64. Своего рода универсальное разложение
Все равно не понятно.
«Теперь допишем множители из второго разложения, которых нет в первом разложении»
3-ка присутствует в первом разложении.
не могу вообще понять НОДа и нОКА
Очень полезный сайт. Теперь смогу помогать сыну по математике. Спасибо вам за ваш труд.
Третий способ нахождения НОК бессмысленный. Зачем что то перемножать и делить, если уже есть множители обоих чисел, полученные при нахождении НОД? Проще объединить их.
Большое вам спасибо! Все объяснения очень понятны! Но как правильно заметил sayanlev, эту тему надо осваивать не спеша, с повторением.
Спасибо большое за сайт! Очень помогает
В 11 упражнении ошибка, 4:2=2
В одном из примеров НОД 36 и 48 =12 а разве не 6?
36 : 12 = 3
48 : 12 = 4
6 является делителем чисел 36 и 48, но не является наибольшим для них.
Наибольшим является 12.
Здравствуйте!
А может быть такое, что при разложении двух чисел, и нахождении общих множителей, и перемноживании найденных множителей наибольший общий делитель будет найден неправильно?
Да, если умножение выполнено неправильно.
А какой НОД у чисел 26 и 64?
https://ibb.co/j8nyp6t — ссылка на то, как решал я (картинка)
НОД (26; 64) = 2
Но почему хотя бы не 4, ведь 2 — общий простой множитель?
Наибольший общий делитель должен позволять разделить на себя оба числа без остатка. Числа 26 и 64 нельзя разделить на 4 без остатка. Поэтому число 4 не является наибольшим общим делителем.
Множитель 2 входит в оба разложения только один раз. Итогового произведения простых множителей как такового не будет. Общий простой множитель это просто 2. Он же наибольший общий делитель. Вот если бы двойка входила два раза в оба разложения, тогда НОД был бы 4.
Например, НОД (4; 8) = 4
2 * 2 = 4
Признателен за детальные ответы.
P.S. Да, было бы логичнее оставить этот комментарий в ответ на последний комментарий от вас, но там нет кнопки «Ответить».
184, 28 и 38 найдите НОД и НОК
НОД (184; 28; 38) = 2
НОК (184; 28; 38) = 24472
День добрый, хотелось бы узнать универсальную формулу определения НОК для 3-х, 4-х дву-трезначных чисел, как существующую для 2-х чисел: НОК = (a*b)НОД. Существует такая в природе? При разложении многозначных чисел и вычислении НОК могут возникать математические ошибки в силу большого количества цифр!!! Для наглядности понимания значения НОК в параллельных источниках нашел задачу про шаги взрослого и ребенка. Нужно было определить расстояние на котором их следы совпадут после начала движения. Хотелось бы видеть у вас побольше примеров прикладного характера. Спасибо!
Здравствуйте. Как решить нод НОК если идут степени
2^3 4^2 как делать каким способом?
При нахождении НОК, нам нужно выписать с второго разложения цифры которых нет в первом разложении. Но почему так получается, что 2 есть в первом разложении, но при этом она ещё раз выписывается со второго разложения в первое? По какому принципу нужно выписать эти цифры?
Цифры нужно выписать так, чтобы получилось разложение в которое входят множители обоих чисел.
Блин! Кто знает где можно найти линейное представление НОД и НОК! и т.п.
В тексте ничего не сказано для чего вообще нужны НОД и НОК и зачем их искать. Т.е. необходимо было объяснить именно практическое применение этих терминов. Например, НОД пригодился бы при сокращении дроби, которую можно сократить (и числитель, и знаменатель) на НОД, а НОК при приведении дробей под общий знаменатель, знаменателем как раз и будет НОК.
У тебя 12 яблок и 9 конфет сколько человек понадобится чтобы все это разделить поровну? Вот тебе и нужен нод.
Об этом рассказано в следующих уроках, чтобы не отпугивать учеников. А так, в начале урока сказано, что не поняв НОД и НОК, невозможно понять дроби.
Все классно, но добавьте пример где применить в жизни. Не ошибусь если из тех кто тут оставил комментарий 95% понятие не имеют, где им это понадобится.
Об этом рассказано в следующих уроках, чтобы не отпугивать учеников.
Здравствуйте, третий способ второй пример я решил вторым способом и у меня получилось 10,2*5=10,но не 20!Или нужно подбирать способы по-обстоятельствам?
Здравствуйте.
Способ можно выбирать любой. Ответы должны совпадать.
2 * 2 * 5 = 20
Здравствуйте! Помогите с заданием №7, я делал так.
98/2 35/3
48/7 15/3
7/7 5/5
1 1
Почему при делении 35ти используется 5???
35 на 3 не дéлится без остатка. Поэтому используется деление на 5. Делить нужно только на простые множители.
Эх, уже в колледже учусь на программиста, а математику вообще не знаю. Приходится учить 🙂
Знаю как находить от любых чисел НОД и НОК, и с легкостью манипулировать с дробями (с разными знаменателями) машинально. В чем заключается суть механизма НОД и НОК?
Даже в таких задачах не улавливаю смысла НОК и НОД:
1.Садовой участок размером 54×48 М по периметру необходимо оградить забором,для этого через равные промежутки надо поставить бетонные столбы.Сколько столбов необходимо привезти для участка,и на каком максимальном расстоянии друг от друга будут стоять столбы?
2.Вдоль дороги от пункта А поставлены столбы через каждые 45м. Эти столбы решили заменить другими, поставив их на расстоянии 60 м друг от друга. Найдите расстояние от пункта А до ближайшего столба,который будет стоять на месте старого.
Может я тупой?
Нахождение НОД и НОК
Алгоритм(Евклида) нахождения НОД делением
Большее число делим на меньшее.
Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
Если есть остаток, то большее число заменяем на остаток от деления.
Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6
а нужно обязательно знать все 3 способа ?
Необязательно. Достаточно знать любой, который больше нравится
Друзья, я понимаю, что автор не дает более легкой для запоминания формулы вычисления НОД, поскольку мы еще вроде как не проходили степени. Но мы же их знаем. И правило нахождения НОД и для двух, и для трех и, наверное, более чисел звучит так: нод = произведению простых множителей, взятых в наименьшей степени. Вот пример: ищем НОД 18, 48, 96.
У 18 — 2*3*3. Это значит 2 в первой степени * на 3 в квадрате (не знаю, как степени написать)
У 48 — 2*2*2*2*3. Это значит 2 в 4-й степени * на 3 в первой степени
У 96 — 2*2*2*2*2*3. То есть 2 в 5-й степени умножить на 3 в первой степени. Общие множители — 2 и 3. Наименьшая степень — первая и у двойки и у тройки. Значит НОД = 2 в первой степени умножить на 3 в в первой степени. То есть 2*3=6.
Как решить эту задачу
Найти НОД и НОК?
a=2×2×2×3×3×5×7 в=2×2×3×5×7
Для НОК тоже есть правило со степенями: Чтобы вычислить НОК, нужно перемножить наибольшие степени всех встречающихся множителей (не только общих).
Автору курса ОГРОМНОЕ СПАСИБО!
А можете решение покозать
Я просто чуть не понял
Добавьте добавление комментариев до самих комментариев, тк долго и неудобно отстать вниз, что бы оставить комментарий после урока.
Как не странно, затруднения возникло не в самой теме урока и их примерах, щелкал как орешки, а при проверка НОК последнего примера для числа 24. Из за невнимательности неправильно просчитал 3192 поделить на 24. При делении 31 на 24 перенёс единицу из десятка, но забыл её убрать:) Так что изучайте и посторяйте тщательно все темы предыдущих уроков. Ну и внимание, под конец подустал видимо немнога, если решать все примеры за один заход с обратной проверкой НОД и НОК)
Благодарю за урок. А то при изучении программирования, я слышал НОД и НОК и думал, что это за таинственные незнакомцы.
В школе, не смотря на Физ мат класс, изучал математику на другом языке, по этому и возникло данное любопытство к данной теме.
Благодарю. Так держать! =)!
Боже, до меня дошло, неужели это из программы за 6 класс, страшно подумать что будет дальше). Огромное спасибо за данный материал
Здравствуйте. Объясните, пожалуйста, почему при разложении числа 24 на множители мы используем делитель 2 и 3? почему не используем, на пример, 4?
Потому что 4 можно разложить на 2 и 2, вн нам нужны простые (не разлагаемые) делители
вообще то это объясняют в 5 классе
Почти меня потеряли. Раньше три темы в день. Сейчас три дня на тему… пришлось вдогонку смотреть видосы на ютубчтике. Какой-то парниша показал, как решать, возводя простые множители в степени. Бинго. Дошло теперь
Спасибо, очень хорошо объяснили)))
Супер понятно! Спасибо
Добрый вечер, запутался.
Числа: 28, 24, 76
НОД нашел: 4
НОК = (28*24*76)/4=12768
12768/28=456
12768/24=532
12768/76=168
В ответах НОК = 3192
Где ошибка? Спасибо заранее!
Не могу понять как найти НОК. Как знать сколько или какие числа добавлять к первому разложению? Вот почему например: в примере 2 мы добавляем две тройки, а в третьем одну? (хотя там же находится еще одна). Пожалуйста, если не поняли вопрос уточните у меня, мне правда хочется понять как решать НОК вторым способом. Извините за глупый вопрос.
Здравствуйте, пожалуйста объясните мне как найти НОК вторым способом. Я не понимаю когда и какие простые числа нужна составлять с первым разложением. «Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.» А как понять каких именно не хватает? Какие дописывать, а какие нет? Извините за глупый вопрос я в математике тот еще валенок :p. Если не поняли вопрос уточните у меня пожалуйста.
Ааааа всё я понял. В инете пошарился и дошло. Извините что два раза написал, я думал то сообщение пропало. Спасибо вам за сайтик, он просто нечто. Цмок :#
Здравствуйте.
Скажите пожалуйста, третий способ нахождения НОК для трех чисел выходит не работает? только для двух?
И существует ли тогда одновременный способ нахождения НОД и НОК для трех чисел, при условии , если так же известен НОД этих трех чисел?
Просто ОГРОМНЕЙШЕЕ спасибо автору за объяснение! Попробую ученикам объяснить вашим способом. Может так до них дойдет?
Спасиб, теперь я написал программу для решения нок и нод, просто выполняю задания из проекта Эйлера
Кстати 232792560 это самое маленькое число, на которое делятся все числа от 1 до 20
Здравствуйте. Напишите, пожалуйста, у вас есть книга или вся информация по изучению математики 5-9 класс. Я бы купила ее. Так вы хорошо все обьясняете. Хочу стать учителем по математике.
Или посоветуйте, пожалуйста, хорошие учебники по изучению тем математики. Благодарю заранее за ответ.
Здравствуйте.
Книг и информации к сожалению нету. Уроки на сайте создаём опираясь на свой опыт и университетские лекции.
Из хороших книг по математике можем посоветовать учебники Киселёва А.П.
Добрый день! Не совсем понятно, как вы выписываете множители (по какому принципу), когда высчитывается НОК из 3 чисел. Например «Задание 12. Найдите НОК чисел 24, 48, 64», где у вас получается 2х2х2х2х2х2х2х3, хотя изначально у вас идёт пояснение, что выписывается разложение из первого числа т.е. 24 = 2х2х2х3 и каким образом совмещается с числами из двух других разложений, где 48=2х2х2х2х3 и 64=2х2х2х2х2х2
У меня, почему то, получается НОК = 1152, если следовать логики показанной вам методики разложения на множители.
Буду очень признателен за обратную связь!
Добрый день. У вас ошибка в комментарии (или опечатка) — одна двойка лишняя.
Выписываете первое разложение и дописываете туда множители из других разложений, которых нет в первом разложении
Ваше разложение должно работать так — в любой момент у вас должна быть возможность получить любое из чисел: 24, 48 и 64, путем перемножения множителей
Спасибо! Здесь я понял логику, но в то же время не понимаю, как (например) формируется выражение в примере НОК 18,48,96, где: 18=2х3х3; 48=2х2х2х2х3; 96=2х2х2х2х2х3 т.е. выписываем первую раскладку 2х3х3 из второй раскладки берём 2х2 или 2х3?, а из третьей 2х2х2 или 2х2х3.
У вас в решении получается выражение: 2х3х3х2х2х2х2 = … Как понять суть формирования этого выражения из 3х разборов по множителям.
Может я ошибочно пытаюсь найти логику, когда есть закономерный алгоритм действий.
Из второй раскладки берёте 2х2х2, а из третьей раскладки только одну двойку.
2 х 3 х 3 х 2 х 2 х 2 х 2
Получается итоговое разложение которое включает в себя множители чисел 18, 48, 96.
Разложение 2×3×3×2×2×2×2 и включает в себя множители этих чисел.
Примерно так это можно себе представить
НОД — наибольший общий делитель. Почему именно наибольший, а не наименьший? Почему для чисел 54 и 86 нод будет 2, а не 4 к примеру?
54:4=13(2 В ОСТАТКЕ) (54 НЕ РАЗДЕЛИЛОСЬ на 4 БЕЗ ОСТАТКА, значит число 4 НЕ ЯВЛЯЕТСЯ делителем числа 54)
54:2=27, 86:2=43. НОД (54 и 86)=2.
a и b, то есть 54 и 86 делятся без остатка на 2. Наибольший ОБЩИЙ делитель чисел 54 и 86 равен числу 2.
100 и 86, 100:4=25, 86:4=21(ост2)
Да только 2
54:4= не 13 в ост 2 а 13 ост 5, проверьте свой пример заново
Кто разбирается, можете написать несколько примеров (чем больше тем лучше) где это все в жизни применяется? Возможно про это будет дальше, но сейчас тоже хотелось бы узнать, чтобы сильнее замотивировать себя. Просто примеры, без решений
НОД — 2 и 3 способ одно и то же, только во втором случае мы делаем это в уме
Добрый день! Не перестаю удивляться тому, как придумывают новые способы, чтобы запутать детей. Мы учили дроби, сокращали, приводили к общему знаменателю, не имея понятия об этой «дурке» под названием НОК и НОД! Столько сил и времени уходит на освоение этих понятий, без которых и так всё ясно. Огромное спасибо ребятам, приславшим примеры и объяснения к ним, потому что приходится разбираться самой и впихивать это в головы детей.
Вы прогуляли просто
—
при ответе на мой E-mail, указывать ссылку на моё сообщение
mowgly-10@yandex.ru
НОД (54 и 68) почему 2?
Ведь 54 равна 2*3*3*3 а 86 равна 2*43
Во втором способе сказано что найти общие делители и УМНОЖИТЬ их, если умножить 2 на 2 то получается 4, а двойка откуда взялась? Объясните пожалуйста
Так 68, или 86?
Насколько я в восторге от обучения не передать словами. В школе математика в основном для меня была темным лесом. А сейчас, изучая математику на данном сайте я начинаю понимать как этот темный лес устроен. Хочется изучать и изучать дальше. Спасибо огромное автору данного ресурса за его работу. Как оказалось для того чтобы изучить математику с нуля не нужно снова идти в школу, нужно просто уметь донести информацию хотя бы в текстовом виде.
Спасибо админам за сайт. Все круто но что то пока не понимаю как находить НОК. если нужно найти НОК двух чисел то нахожу а если три и более то нет. Не совсем понятен алгоритм
Нифига не понял 14 задание.
Где мы взяли еще 4 двойки в конце ?
Огромное спасибо! Очень часто обращаюсь к Вашим урокам. За 3 года 3 учителя по математике у ребенка. И многое детям объясняют на бегу или не объясняют вовсе. Благодаря Вашим урокам могу объяснить ребёнку то, что он не понимает
Первая тема на которой немного стопорнулся, в итоге на второй день ещё раз, более полно (не пропуская примеры) всё прорешал и все дошло, так что не отчаивайтесь пацаны, упорно решайте все примеры и вперед дальше.
На примере 112 и 82 перепутал числа и искал НОД и НОК для 112 и 88.
Ответ:
НОД = 8
НОК = 1232
Правильно?
Здравствуйте!
Объясните, пожалуйста, почему когда ищем нок первым способом (в примере для 9 и 12), то кратные 9 пишем до 9×9, а кратные 12×12? а не до 12×9 (что точно будет наименьшим кратным, если у чисел нет общих делителей) зачем идти до 12×12?
Огромное спасибо Вам! Оказывается все так просто! Я столько мучилась с математикой. Респект Вам.
Доброго времени суток! Запутался немного. Могли бы объяснить почему в задании 2 «Найдите НОК чисел 12 и 16» в разложение добавляются ещё две двойки со второго разложения? Почему тогда в примере поиска НОК (где ищется НОК для 12 и 9) Не добавляется еще одна тройка со второго разложения?
Я обещала себе заниматься каждый день математикой, т.к хочу сдать экзамен и получить красный диплом. Мне всегда было интересно, почему и как люди понимают эту незаурядную науку. И вот я на пути этого понимания. Этот урок для меня был сложным в плане усидчивости и внимания. Я прошла его и проходила долго.
Мне очень нравится читать комментарии о том, как у людей получается пройти тему и меня это очень вдохновляет.
Спасибо большое за сайт! Как хорошо, что люди осознают проблему сложности понимания математики у других, и делают все, чтобы сделать мир лучше
Что-что, а вот назвать математику «незаурядной» язык не поворачивается.
Блин, год назад остановилась на этой теме. Самое время продолжать 🙂
Не совсем понимаю, по какому принципу из разложенных множителей формируется выражение для определения НОК. мы выписываем множители полученные из ПЕРВОГО числа, а из ВТОРОГО и ТРЕТЬЕГО выписываем те множители, которые не совпадают с множителями из ПЕРВОГО числа, так получается?