В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.
Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.
Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:
10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1
Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто как 2 + 2 или 9 − 3.
Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.
Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:
Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1
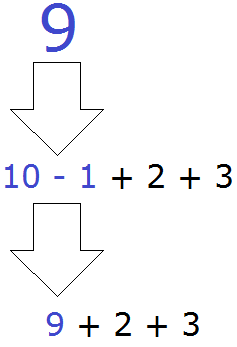
Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:
1. Сначала вычислить то, что находится в скобках!
2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!
3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!
Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:
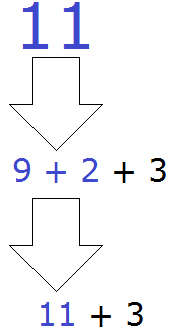
Осталось простейшее выражение 11 + 3, которое вычисляется легко:
11 + 3 = 14
Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14
10 − 1 + 2 + 3 = 14
Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:
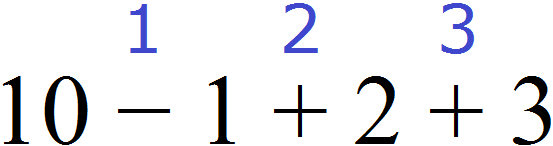
И далее можно выполнить действия по отдельности, что очень удобно:
1) 10 − 1 = 9
2) 9 + 2 = 11
3) 11 + 3 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:
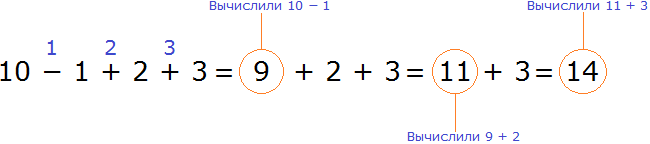
Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.
Пример 2. Найти значение выражения (3 + 5) + 2 × 3
Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:
8 + 2 × 3
Снова читаем первое правило:
Сначала вычислить то, что находится в скобках!
Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3
8 + 6
Осталось простейшее выражение 8 + 6, которое вычисляется легко:
8 + 6 = 14
Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14
(3 + 5) + 2 × 3 = 14
Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:
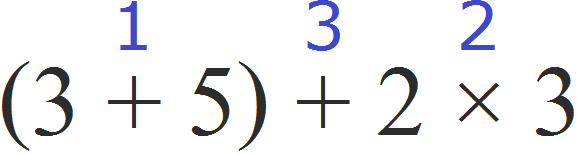
И далее можно выполнить действия по отдельности, что очень удобно:
1) 3 + 5 = 8
2) 2 × 3 = 6
3) 8 + 6 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
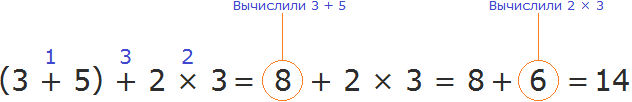
Но опять же, используя такой способ, нужно быть очень внимательным.
Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1
Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:
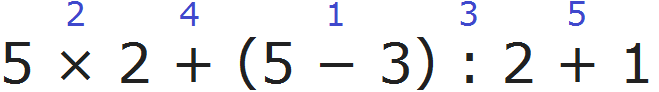
1) 5 − 3 = 2
2) 5 × 2 = 10
3) 2 : 2 = 1
4) 10 + 1 = 11
5) 11 + 1 = 12
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.
Пример 4. Найти значение выражения (3250 − 2905) : 5
Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым
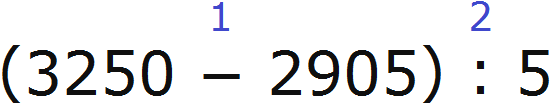
1) 3250 − 2905 = 345
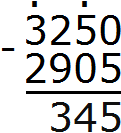
2) 345 : 5 = 69
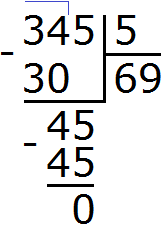
В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.
Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.
В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.
В результате будем иметь следующий порядок:
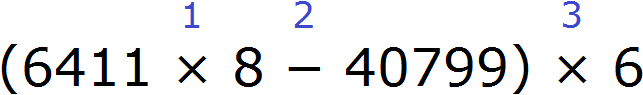
1) 6 411 × 8 = 51 288
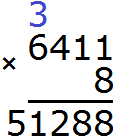
2) 51 288 − 40 799 = 10 489

3) 10 489 × 6 = 62 934
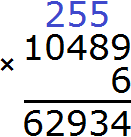
Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)
Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.
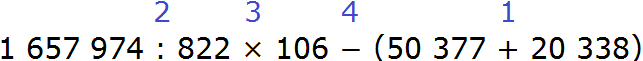
1) 50 377 + 20 338 = 70 715
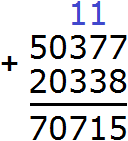
2) 1 657 974 : 822 = 2 017
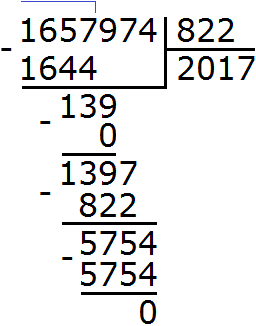
3) 2 017 × 106 = 213 802
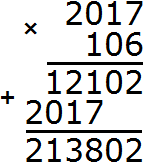
4) 213 802−70 715 = 143 087
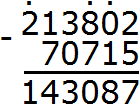
Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.
В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:
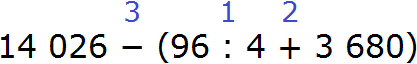
1) 96 : 4 = 24
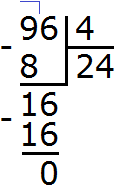
2) 24 + 3 680 = 3 704
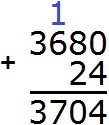
3) 14026 − 3 704 = 10 322
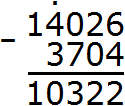
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
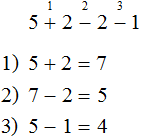
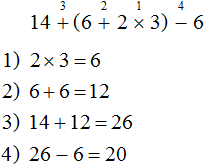
Спасибо.
Спасибо автору
Спасибо) Всё удобно и ясно.))
Спасибо автору! Всё ясно и просто)))
А где ссылка на официальную инфлрмацию по порядку действий?
Освежаю школьную программу в памяти и хочу сказать автору огромное спасибо!
Круто! все просто! спасибо!
Спасибо! перестал понимать с пятого класса) на этом и остановился) а тут занялся фундаментальным анализом на фондовой бирже) а там одни формулы)
Круто-круто, звучит солидно, желаю удачи в развитии навыков
Очень спасибо , вы делаете очень полезную работу , а геометрию проходить будете?
Спасибо! Сайт очень понравился. Урок тоже.
Если есть вопросы задавать в коментах или куда-то еще можно написать?
Здравствуйте, скажите пожалуйста, я попытался решить задание #4 своим путём, и ответ у меня получился другой. Решал так 756:((3:4)*28)=756:(0.75*28)=756:21=36. Почему ответ другой, ведь операции деления и умножения между собой равны, следовательно могут выполняться в любом порядке. Что я не так понял?
Здравствуйте.
Операции можно выполнять в любом порядке, если выражение состоит из нескольких сомножителей. Это сочетательный закон умножения.
А если же выражение состоит из деления и умножения, то операции надо выполнять слева направо в порядке их следования.
Записать так 756:((3:4)*28) можно было бы, если бы исходное выражение было дано в виде 756*3*4*28.
С какого перепуга ты взял их в скобки
Потому что 756:3:4=756:(3*4), а не 756:(3:4). Операции деления и умножения могут выполняться в любом порядке, а вот скобки вводить произвольным образом — нельзя.
Потому что, выполняя действия в другом порядке, вы получаете совершенно другие цифры. Операции деления и умножения абсолютно не равны, следовательно, в любом порядке рашться не могут. Поэтому решать необходимо в соответствии с написанным примером, а не ставить скобки самостоятельно.
756 : 3 =252
252 : 4 = 63
63 х 28 = 1764
Здравствуйте! высчитайте это выражение 6:2*(1+2)=?
Здравствуйте!
Разбирали уже. По правилам математики 9. Но в пособиях по физике такая запись иногда понимается как 1. Для устранения неоднозначности в таких случаях рекомендуется использовать скобки.
6:2*(1+2)=9,
6:2(1+2)=1
Добрый день. Спасибо за объяснения. Если бы у меня в детстве был такой учитель как вы, это очень многое бы поменяло! Я готова даже внести пожертвование, лишь бы вы выложили побольше уроков, включая и геометрию тоже.
Большое спасибо за ваши уроки. Очень полезный курс
Благодарю за курс! Очень удобно, чередуются сложные темы с простыми.
Просто восхищаюсь проделанной работой авторов этого курса! Это потрясающий ресурс! Лучший в своем направлении!
у меня через 2 года егэ, а я учу деление. Будь проклята моя училка
Для них всех отдельный котёл в аду будет!
Почему??
Спасибо, за проделанную вами работу для нас!)
Нельзя проклинать! Не всякий человек способен быть учителем, но может выбрать такую профессию. В школе другая обстановка, другой подход. Часто ученики балбесы. Не хотят учиться, бояться лишний раз спросить, а потом учитель виноват.
Ну да, виновата не халатность учителей, не их пофигизм, не их простое желание денег заработать, а именно дети, которым объясняют так, что половина не понимает (а если не понял и подошёл спросил — твои проблемы, раз не понял)..
Автор, спасибо Вам большое за труд.
Спасибо, двигаемся дальше).
у меня через 1,5 года ЕГЭ , вот и будем сдавать вместе .
Немного запутался, в примере 213802-70715=143087 , в данном выражении вычитание производится путем превращения в разряде сотен — 80 в 79 и отнимается число 71? В решении над нулем стоит точка, но у ноля ведь для 2 мы занять еденицу ведь не сможем?
На самом простейшем языке разложено всё. Даже кнопочка удобная в правом нижнем углу, чтобы быстро подняться вверх по странице.
Хах, я даже не заметила эту кнопку, пока вы не сказали
Гигантское спасибо, за полезный контент. Для меня большое значение имеет то, что вы делаете и делаете это на благотворительной основе, так как не у всех есть возможность платить за столь грамотно собранный материал. Обязательно поддержу донатом, как появится возможность.
Спасибо большое!
мне 34 года и вот пригодилась математика в жизни. И я поняла, что ничего не знаю, к своему стыду. Спасибо огромное за ваш сайт. Восполняю пробелы и даже подумать не могла, что это настолько увлекательно.
Спасибо ещё раз!
Спасибо!
Отлично преподнесено. Разжевано и помещено прямиком в мозг. Добавьте способ доната с банковской карты.
Какой будет ответ в этом примере
10-10×10+10
У меня получилось 100, но друзья говорят что это не правильный ответ
10 — 10 * 10 + 10 = -80
1) 10 * 10 = 100
2) 10 — 100 = -90
3) -90 + 10 = -80
в firefox и все браузера на движке хром:
правая кнопка мыши -> исследовать элемент -> консоль
Пишешь туда любое числовое выражение и получишь правильный ответ, если не произойдёт переполнение в программе переменных.
Если нужны подробности, это программирование на языке JavaScript
Ответ -8 0
Запустил математику еще во 2 или 3 классе. Был двоечник. Сейчас мне 34 и я хочу начать сначала.
Если бы в школе раздавали такие материалы, учиться было бы гораздо легче, и такие как я не отставали бы от остальных учеников.
Я из тех, кому нужно все разжевать, показать, а не решить пару раз у доски и перейти к следующему.
Я долго не мог начать изучать программирование, потому что большинство книг не «разжевывает» так же подробно как у вас на сайте, и дальше «hello world» не сдвигалось, пока не попалась однажды хорошая книга, где так же как у вас на сайте, все объяснили доступным языком для совсем «нулёвых».
Ваш сайт для меня большая ценность.
Подскажите, что это за книга по программированию, в которой всё объяснили доступным языком.
Что за книга по программированию?
Заинтриговали, что за книга ?
Дмитрий, что это за книга по программированию?
Спасибо!
Не спойлери 🙂
неужели я один заметил ошибку в примере 50377+20388?
Будьте внимательней. У автора в примере не: 20 388, а: 20 338
1. Скобки
2. Степень
3. Умножение/деление
4. Сложение/вычитания
Потрясающе просто изучать математику по вашему сайту, нигде больше такого не видела! Вы — явно мастер своего дела!
Спасибо автору, всё понятно разложено, решаю на одном дыхание.
Можно ссылку на источник по поводу однозначности выполнения деления и умножения по приоритету слева направо?
На пример, всем известный пример:
6 / 2(6 — 2)
по вашему это эквивалентно
(6 / 2)(6 — 4) = 3 * 2 = 6
но по факту это дробь
6 / 2 * (6 — 4) = 6 / 8 = 0.75
Ссылка на источник (учебник, может быть) поможет нам разобраться.
Пон
с малых лет перестал понимать математику. читаю внимательно и восполняю пустоту. написано очень доступно. надеюсь, что мне хватит ума освоить весь материал. потом буду осваивать русский язык Спасибо большое за очень хорошо проделанную работу
Спасибо большое вашему сайту, я раньше думала что умственно отсталая какая-то, без шуток я ОГЭ сдала на 2, даже в столбик делить не умела, выросла с горем пополам закончила колледж, математику чисто просто из жалости поставили 3, сейчас 25 для себя пытаюсь разобраться с этим прекрасным предметом, как разберусь пойму что понимаю азы, поступлю на высшее
Дай бог вам здоровья за эту работу, не один репетитор не моя тётя математик не могли мне это вдолбить, а тут я буквально прозрела