Продолжаем изучать основы алгебры. В данном уроке мы научимся раскрывать скобки в выражениях. Раскрыть скобки означает избавить выражение от этих скобок.
Чтобы раскрывать скобки, нужно выучить наизусть два правила. При регулярных занятиях раскрывать скобки можно с закрытыми глазами, и про те правила которые требовалось заучивать наизусть, можно благополучно забыть.
Первое правило раскрытия скобок
Рассмотрим следующее выражение:
8 + (−9 + 3)
Значение данного выражения равно 2. Раскроем скобки в данном выражении. Раскрыть скобки означает избавиться от них, не влияя на значение выражения. То есть после избавления от скобок значение выражения 8 + (−9 + 3) по прежнему должно быть равно двум.
Первое правило раскрытия скобок выглядит следующим образом:
При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.
Итак, мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Этот плюс нужно опустить вместе со скобками. Иными словами, скобки исчезнут вместе с плюсом, который перед ними стоял. А то, что было в скобках запишется без изменений:

Мы получили выражение без скобок 8−9+3. Данное выражение равно 2, как и предыдущее выражение со скобками было равно 2.
8 + (−9 + 3) = 2
8 − 9 + 3 = 2
Таким образом, между выражениями 8+(−9+3) и 8−9+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
8 + (−9 + 3) = 8 − 9 + 3
2 = 2
Пример 2. Раскрыть скобки в выражении 3 + (−1 − 4)
Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:
3 + (−1 − 4) = 3 − 1 − 4
Пример 3. Раскрыть скобки в выражении 2 + (−1)
Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:
2 + (−1) = 2 − 1
В данном примере раскрытие скобок стало своего рода обратной операцией замене вычитания сложением. Как это понимать?
В выражении 2 − 1 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 2 + (−1). Но если в выражении 2 + (−1) раскрыть скобки, то получится изначальное 2 − 1.
Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после каких-нибудь преобразований. То есть избавить его от скобок и сделать проще.
Например, упростим выражение 2a + a− 5b + b.
Чтобы упростить данное выражение, можно привести подобные слагаемые. Напомним, что для приведения подобных слагаемых, нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:
![]()
Получили выражение 3a + (−4b). В этом выражении раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок, то есть опускаем скобки вместе с плюсом, который стоит перед этими скобками:
3a + (−4b) = 3a − 4b
Таким образом, выражение 2a+a−5b+b упрощается до 3a−4b.
Раскрыв одни скобки, по пути могут встретиться другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в следующем выражении:
2 + (−3 + 1) + 3 + (−6)
Здесь два места, где нужно раскрыть скобки. В данном случае применимо первое правило раскрытия скобок, а именно опускание скобок вместе с плюсом, который стоит перед этими скобками:
2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6
Пример 3. Раскрыть скобки в выражении 6+(−3)+(−2)
В обоих местах, где имеются скобки, перед ними стоит плюс. Здесь опять же применяется первое правило раскрытия скобок:
6 + (−3) + (−2) = 6 − 3 − 2
Иногда первое слагаемое в скобках записано без знака. Например, в выражении 1+(2+3−4) первое слагаемое в скобках 2 записано без знака. Возникает вопрос, а какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ напрашивается сам — перед двойкой будет стоять плюс.
На самом деле даже будучи в скобках перед двойкой стоит плюс, но мы его не видим по причине того, что его не записывают. Мы уже говорили, что полная запись положительных чисел выглядит как +1, +2, +3. Но плюсы по традиции не записывают, поэтому мы и видим привычные для нас положительные числа 1, 2, 3.
Поэтому, чтобы раскрыть скобки в выражении 1+(2+3−4), нужно как обычно опустить скобки вместе с плюсом, стоящим перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:
1 + (2 + 3 − 4) = 1 + 2 + 3 − 4
Пример 4. Раскрыть скобки в выражении −5 + (2 − 3)
Перед скобками стоит плюс, поэтому применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед этими скобками. Но первое слагаемое, которое в скобках записываем со знаком плюс:
−5 + (2 − 3) = −5 + 2 − 3
Пример 5. Раскрыть скобки в выражении (−5)
Перед скобками стоит плюс, но он не записан по причине того, что до него не было других чисел или выражений. Наша задача убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он невидим)
(−5) = −5
Пример 6. Раскрыть скобки в выражении 2a + (−6a + b)
Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:
2a + (−6a + b) = 2a −6a + b
Пример 7. Раскрыть скобки в выражении 5a + (−7b + 6c) + 3a + (−2d)
В данном выражении имеется два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:
5a + (−7b + 6c) + 3a + (−2d) = 5a −7b + 6c + 3a − 2d
Второе правило раскрытия скобок
Теперь рассмотрим второе правило раскрытия скобок. Оно применяется тогда, когда перед скобками стоит минус.
Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный.
Например, раскроем скобки в следующем выражении
5 − (−2 − 3)
Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, стоящим перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Мы получили выражение без скобок 5 + 2 + 3. Данное выражение равно 10, как и предыдущее выражение со скобками было равно 10.
5 − (−2 − 3) = 10
5 + 2 + 3 = 10
Таким образом, между выражениями 5−(−2−3) и 5+2+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 − (−2 − 3) = 5 + 2 + 3
10 = 10
Пример 2. Раскрыть скобки в выражении 6 − (−2 − 5)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок, а именно опускаем скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, записываем с противоположными знаками:
6 − (−2 − 5) = 6 + 2 + 5
Пример 3. Раскрыть скобки в выражении 2 − (7 + 3)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
2 − (7 + 3) = 2 − 7 − 3
Пример 4. Раскрыть скобки в выражении −(−3 + 4)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
−(−3 + 4) = 3 − 4
Пример 5. Раскрыть скобки в выражении −(−8 − 2) + 16 + (−9 − 2)
Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить второе правило раскрытия скобок, а когда очередь доходит до выражения +(−9 − 2) нужно применить первое правило:
−(−8 − 2) + 16 + (−9 − 2) = 8 + 2 + 16 − 9 − 2
Пример 6. Раскрыть скобки в выражении −(−a − 1)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
−(−a − 1) = a + 1
Пример 7. Раскрыть скобки в выражении −(4a + 3)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
−(4a + 3) = −4a − 3
Пример 8. Раскрыть скобки в выражении a − (4b + 3) + 15
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
a − (4b + 3) + 15 = a − 4b − 3 + 15
Пример 9. Раскрыть скобки в выражении 2a + (3b − b) − (3c + 5)
Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить первое правило раскрытия скобок, а когда очередь доходит до выражения −(3c+5) нужно применить второе правило:
2a + (3b − b) − (3c + 5) = 2a + 3b − b − 3c − 5
Пример 10. Раскрыть скобки в выражении −a − (−4a) + (−6b) − (−8c + 15)
Здесь три места, где нужно раскрыть скобки. Вначале нужно применить второе правило раскрытия скобок, затем первое, а затем опять второе:
−a − (−4a) + (−6b) − (−8c + 15) = −a + 4a − 6b + 8c − 15
Механизм раскрытия скобок
Правила раскрытия скобок, которые мы сейчас рассмотрели, основаны на распределительном законе умножения:
a(b + c) = ab + ac
На самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)
3 × (4 + 5) = 3 × 4 + 3 × 5
Поэтому, если нужно умножить число на выражение в скобках (или выражение в скобках умножить на число) надо говорить раскроем скобки.
Но как связан распределительный закон умножения с правилами раскрытия скобок, которые мы рассматривали ранее?
Дело в том, что перед любыми скобками стоит общий множитель. В примере 3 × (4 + 5) общий множитель это 3. А в примере a(b + c) общий множитель это переменная a.
Если перед скобками нет чисел или переменных, то общим множителем является 1 или −1, в зависимости от того, какой знак стоит перед скобками. Если перед скобками стоит плюс, значит общим множителем является 1. Если перед скобками стоит минус, значит общим множителем является −1.
К примеру, раскроем скобки в выражении −(3b − 1). Перед скобками стоит минус, поэтому нужно воспользоваться вторым правилом раскрытия скобок, то есть опустить скобки вместе с минусом, стоящим перед скобками. А выражение, которое было в скобках, записать с противоположными знаками:
−(3b − 1) = −3b + 1
Мы раскрыли скобки, воспользовавшись правилом раскрытия скобок. Но эти же скобки можно раскрыть, воспользовавшись распределительным законом умножения. Для этого сначала записываем перед скобками общий множитель 1, который не был записан:
−1(3b −1)
Минус, который раньше стоял перед скобками относился к этой единице. Теперь можно раскрыть скобки, применяя распределительный закон умножения. Для этого общий множитель −1 нужно умножить на каждое слагаемое в скобках и полученные результаты сложить.
Для удобства заменим разность, находящуюся в скобках на сумму:
−1(3b −1) = −1( 3b + (−1) )
Далее умножаем общий множитель −1 на каждое слагаемое в скобках:
−1(3b −1) = −1(3b + (−1)) = −1 × 3b + (−1) × (−1) = −3b + 1
Как и в прошлый раз мы получили выражение −3b + 1. Каждый согласится с тем, что в этот раз затрачено больше времени на решение столь простейшего примера. Поэтому разумнее пользоваться готовыми правилами раскрытия скобок, которые мы рассматривали в данном уроке:
−(3b − 1) = −3b + 1
Но не мешает знать, как эти правила работают.
В данном уроке мы научились ещё одному тождественному преобразованию. Вместе с раскрытием скобок, вынесением общего за скобки и приведением подобных слагаемых можно немного расширить круг решаемых задач. Например:
Раскрыть скобки и привести подобные слагаемые в следующем выражении:
![]()
Здесь нужно выполнить два действия — сначала раскрыть скобки, а потом привести подобные слагаемые. Итак, по порядку:
1) Раскрываем скобки:
![]()
2) Приводим подобные слагаемые:
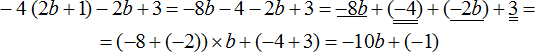
В получившемся выражении −10b+(−1) можно раскрыть скобки:
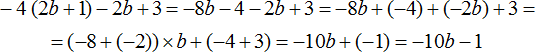
Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:
![]()
1) Раскроем скобки:
![]()
2) Приведем подобные слагаемые. В этот раз для экономии времени и места, не будем записывать, как коэффициенты умножаются на общую буквенную часть
![]()
Пример 3. Упростить выражение 8m+3m и найти его значение при m=−4
1) Сначала упростим выражение. Чтобы упростить выражение 8m+3m, можно вынести в нём общий множитель m за скобки:
8m + 3m = m(8 + 3)
2) Находим значение выражения m(8 + 3) при m = −4. Для этого в выражение m(8 + 3) вместо переменной m подставляем число −4
m (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
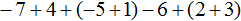
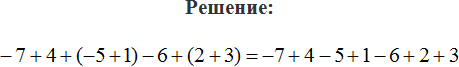
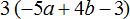
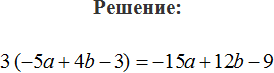
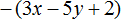
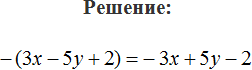
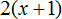
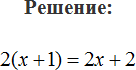
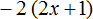
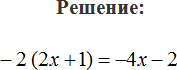
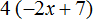
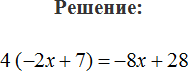
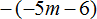
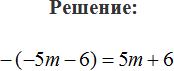
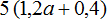
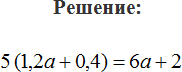
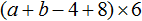
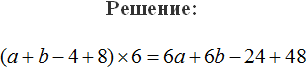
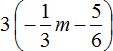
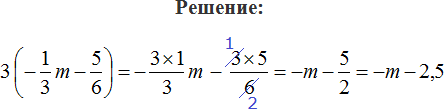
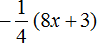

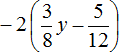

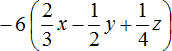
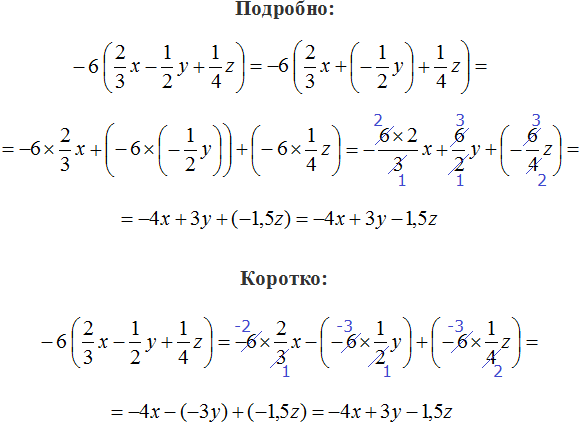
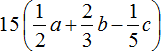
Ваши уроки еще будут выходить?
огромнейшее спасибо admin, а когда будут новые уроки?
жду с нетерпением)
Спасибо огромное за шикарные уроки!
Очень жаль, что уроки выходят так редко. Придется качать учебники и читать, хоть я и занимаюсь просто ради интереса, для себя, но каждое утро неистовое желание и интерес узнать что же там дальше.
Я все равно буду следить за выходом новых шагов и читать свежие уроки, так как вы умеете красиво и понятно подать материал.
Еще раз спасибо за отлично проведенное время и успехов Вам.
Когда будут новые уроки?
Здравствуйте! Админ когда обновление будет?
Спасибо за уроки. Ждём новых уроков.
Жду новых уроков!
Когда следующий урок? Говорили, что работа заморожена над сайтом, но так же сказали, что уроки будут выходить раз в месяц, а последний урок вышел судя по посту ВК в апреле, а уже сентябрь!?=(
Администраторы, веб программисты этого сайта, обращаю ваше внимание, что слева в контекстном меню и на главной странице сайта, после 42 шага, отсутствуют ссылки на следующие уроки, например про Простейшие Задачи и так далее. Доработайте кликабельные ссылки пожалуйста.
Сохраняю страницы к себе в архив ПДФ каждой темы, мало ли какие времена настанут с интернетом… Огромное спасибо вам за вашу работу, вы действительно делаете качественно и сердито! Прямо как после лекции «Плач математика»=) Подскажите пожалуйста, если вам известно, имеется ли на просторах интернета подобные сайты вашему, по тематике химии, физики, биологии, возможно вы встречали такое?
Класс. Спасибо большое.
Никак не могла понять одну тему и только здесь поняла!
Здравствуйте. Мне кажется 15 и16 задача одинаковые. Можете этот пост не опубликовать, главное админ получил это 🙂 Спасибо
Очень понравился материал, доступно, понятно. Вы большие молодцы, спасибо!
Решение не правильное.
Спасибо)
Пример 6. Раскрыть скобки в выражении −(−a − 1).
Правильно ли я понимаю что для указанного выражения раскрывать скобки нельзя, т. к. −(−a − 1) ≠ a+1?
Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но то что было в скобках поменяет свой знак на противоположный:
−(−a − 1) = a + 1?
Было: −(−a − 1)
Опустили скобки: − a − 1
Содержимому скобок поменяли знаки на противоположные: a + 1
Большое Спасибо!!!
Не понял третий пример во втором правиле раскрытия скобок там 2-(7+3) там нужно было убрать минус а в скобках сделать замену знаков с плюса на минус
Да, у семёрки же плюс. Когда минус опускается, плюс семерки обращается в минус
А что делать если перед скобками не стоит ни чего а после скобок мы что то отнимаем т.е после скобок стоит знак минус
если перед скобками не стоит ничего, то нужно применять первое правило раскрытия скобок.
Применяется распределительный закон умножения/
(x+2)=x+2 перед скобками всегда есть 1, но её принято не записывать. Выглядеть оно будет так 1*(x+2)=1*x+1*2=1x+2 оно тождественно записи (x+2)=x+2.
Спасибо, всё понятно и просто, огромная благодарность от меня!
Почему ты так решил?
Почему 5 — (-2-3)= 10
не понимаю ничего, вить если -2 + (-3) = 5
5+(-5)= 0
Чтобы сложить отрицательные числа, нужно сложить их модули и перед ответом поставить минус
−2 + (−3) = −5
−2 + (−3) = −2 − 3
5 − (−2 − 3) = 5 − (−5) = 10
Или через раскрытие скобок 5 + 2 + 3 = 10
Да ёлки ! 8:2(2+2)
А если 8:2(3+2)
8÷10=8/10
Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:
5(1-2a)-3(a+1)=5-10a-3a-3
вообще не понятно откуда автор взял 10а и 3, по правилам описанным выше нельзя получить такие числа
5(1-2a)-3(a+1)=5*1-5*2a-3*a-3=5-10a-3a-3. Если что-то не понятно всегда раскладывай.
Привет админ. Почему после раскрытия скобок в выражении 5(1-2a)-3(a+1) получилось 5-10a-3a-3. Почему последний знак это минус а не плюс?(который перед последней тройкой)у меня всегда там плюс получался
Потому что отрицательное число перед скобками -3. Оно имеет такой вид:
-3*a+(-3*1)=-3a-3. Первое правило. Когда перед скобками стоит знак плюс в скобках ничего не меняется. Плюс уходит по скобками, БЫЛО +(-3*1) СТАЛО -3*1 = -3
Админ ответь еще пожалуйста. Может ли быть общий множитель 1 или -1 в выражениях, где минус не один, а перед ним есть число? Например:
7-(3-4). Может ли здесь быть число 1 перед скобкой? Вот так:
7-1(3-4)
а(b-c) =ab-ac,-a(b+c) =-ab-ac.
Или
a(b-c)-d(e+f)=ab-ac-de-df
т.е.
5(1-2a)-3(a+1)=(5×1)-(5×2а)-(3×а)-(3×1)
=5-10а-3а-3
7-1(3-4)Именно так.
7-(3-4) и 7-1(3-4) это РАЗНЫЕ ВЫРАЖЕНИЯ!
7-(3-4)=-21+28
7-1(3-4)=7+(-1(3-4))=7+(-3+4)=7-3+4
Перед скобками стоит скрытая единица если перед скобками никакого числа больше нету. Если там 2(x+2) то единицы скрытой НЕ МОЖЕТ там быть! То есть 2(x+2) НЕ РАВНО 2-1(x+2)
а(b-c) =ab-ac,-a(b+c) =-ab-ac. Или
a(b-c) — d(e+f) =ab-ac-de-df
т.е.
5(1-2a)-3(a+1)=(5×1)-(5×2а)-(3×а)-(3×1)=
=5-10а-3а-3
Извините,можете объяснить?Откуда в -4(2b+1)-2b+3 взялось -8b у вас в раскрытии скобок.Спасибо.
-4*2b=-8b
первое действие при раскрытии скобок
Пожалуйста, объясните откуда взялась 8b в примере в -4(2b+1)-2b+3?
Понимаю, что для Вас это, возможно, лишняя нервотрепка, но для меня это очень важно. Я перечитывал предыдущие уроки, но все равно не совсем понимаю. Отдельно спасибо Вам за ваши труды.
-4 * 2b = -8b
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
Я подумал об этом сперва, но меня смутила последующая четверка после «-8b» (раз мы ее умножили откуда она взялась еще раз?) и я не совсем понял, что произошло с +1. Прошу извинить меня, если мой вопрос очень глупый. Пожалуйста, объясните в более развернутой форме я был бы Вам очень сильно благодарен. Постараюсь больше не беспокоить Вас.
Надеюсь, что вы отнесетесь с пониманием.
Еще раз спасибо Вам за Ваш ответ.
Всего хорошего.
Все я наконец-то додумался 😀
Нужно было -4 умножить на 2b и умножить на +1. Таким образом мы получили -8b — 4. Для меня это было неочевидно поначалу. Скорее всего где-то проморгал.
Спасибо за Ваш ответ.
Спасибо! С дочкой только что решали пример, а я не знал, как объяснить, почему скобки с минусом так раскрываются. Оказывается, там общий множитель +1/-1 подразумевается.
Почему так не разборчиво? Слишком много примеров. Почему вы не объясните сначала правило, ВЫДЕЛЕННОЕ ЯРКИМ ЦВЕТОМ, а потом примеры? У меня нет столько времени на примеры. Вот я сейчас на 48 шаге и не могу понять откуда взялось 12 в этом примере: 4(x + 3) = 16 после раскрытия скобок оно стало 4x+12=16. Откуда 12? Я щас пришла перечитывать урок, но не могу найти нигде этому ответ из-за слишком много примеров! Но а так вы так хорошо все объясняете. ☹️
Это обычное раскрытие скобок 4(x + 3) = 16
Получается:
4 * x = 4x
4 * 3 = 12
4x + 12 = 16
Математика такая вещь, если вы где-то пропустили какую-то тем
то последующие темы Вам будут не понятны.
Сначала изучите распределительный закон умножения.
a(b+c)=a*b+a*c
Подробно Ваш пример выглядит следующим образом:
4(х+3)=4*x+4*3=4x+12=16. И перед переменой если нету никакого числа там стоит скрытая 1, но её принято не записывать, выглядеть оно будет так 4*1x=4x
Пришла перечитывать 41 шаг
Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:
5(1-2a)-3(a+1)=5-10a-3a-3
Как не пытаюсь, не могу понять почему 3а-3, а не 3а+3
перемножая — 3(а+1) , знак минус это ведь знак операции, а не числа, тройка же положительная или нет?
Все никак не могу с этим моментом разобраться, помогите, пожалуйста.
я тоже не могу понять как это так получается
Офигеть вы математики)) скобки раскрываются только в алегбраических выражениях, а в математических вычислениях сначала производятся действия в скобках. 8+(-9+3) будет равно 14, а не 1.
Даже если выполнять действия по порядку, а не с помощью раскрытия скобок, то ответ будет одинаковым. Это следует из правила о тождественном преобразовании, что как бы мы не изменяли и упрощали выражение — ответ не должен измениться. 8+(-9+3)=2
1) -9+3=-6
2) 8+(-6)=2