Наш первый урок назывался числа. Мы рассмотрели лишь малую часть этой темы. На самом деле тема чисел достаточно обширна. В ней много тонкостей и нюансов, много хитростей и интересных фишек.
Сегодня мы продолжим тему чисел, но опять же не будем рассматривать её всю, чтобы не затруднять обучение лишней информацией, которая на первых порах не особо-то и нужна. Мы поговорим о разрядах.
Что такое разряд?
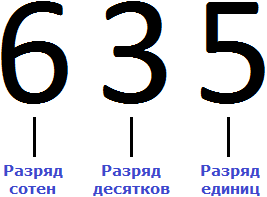
Если говорить простым языком, то разряд это позиция цифры в числе или место, где располагается цифра. Возьмём для примера число 635. Это число состоит из трёх цифр: 6, 3 и 5.
Разряды надо читать справа налево. В числе 635 на первой позиции располагается цифра 5, на второй позиции – цифра 3, на третьей позиции – цифра 6.
Позиция, где располагается цифра 5, называется разрядом единиц
Позиция, где располагается цифра 3, называется разрядом десятков
Позиция, где располагается цифра 6, называется разрядом сотен
Каждый из нас слышал со школы такие вещи как «единицы», «десятки», «сотни». Разряды помимо того что играют роль позиции цифры в числе, сообщают нам некоторую информацию о самом числе. В частности, разряды сообщают нам вес числа. Они сообщают сколько в числе единиц, сколько десятков и сколько сотен.
Вернёмся к нашему числу 635. В разряде единиц располагается пятёрка. О чём это говорит? А говорит это о том, что разряд единиц содержит пять единичек. Выглядит это так:
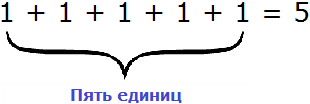
В разряде десятков располагается тройка. Это говорит о том, что разряд десятков содержит три десятка. Выглядит это так:
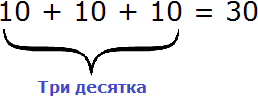
В разряде сотен располагается шестёрка. Это говорит о том, что в разряде сотен располагаются шесть сотен. Выглядит это так:
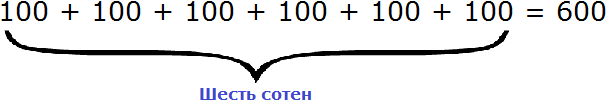
Если сложить число получившихся единиц, число десятков и число сотен, то получим наше изначальное число 635
Существуют и более старшие разряды такие как разряд тысяч, разряд десятков тысяч, разряд сотен тысяч, разряд миллионов и так далее. Такие большие числа мы будем рассматривать редко, но тем не менее о них тоже желательно знать.
Например, в числе 1 645 832 разряд единиц содержит 2 единицы, разряд десятков — 3 десятка, разряд сотен — 8 сотен, разряд тысяч — 5 тысяч, разряд десятков тысяч — 4 десятка тысяч, разряд сотен тысяч — 6 сотен тысяч, разряд миллионов — 1 миллион.
На первых этапах изучения разрядов желательно разбираться сколько единиц, десятков, сотен содержит то или иное число. К примеру, число 9 содержит 9 единиц. Число 12 содержит две единицы и один десяток. Число 123 содержит три единицы, два десятка и одну сотню.
Группировка предметов
После подсчета каких-нибудь предметов, разряды можно использовать для группировки этих предметов. К примеру, если мы насчитали во дворе 35 кирпичей, то можно использовать разряды для группировки этих кирпичей. В случае группировки предметов, разряды можно читать слева направо. Так, цифра 3 в числе 35 будет говорить о том, что в числе 35 содержатся три десятка. А это значит, что 35 кирпичей можно сгруппировать три раза по десять штук.
Итак, сгруппируем кирпичи три раза по десять штук:
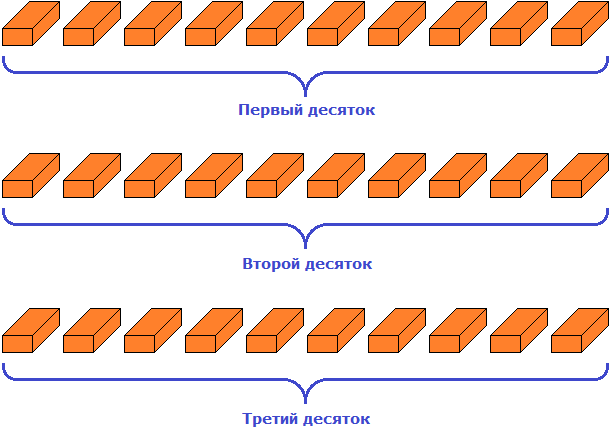
Получилось тридцать кирпичей. Но осталось еще пять единиц кирпичей. Их мы назовем как «пять единиц»
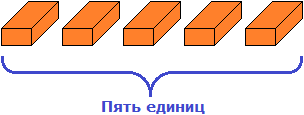
Получилось три десятка и пять единиц кирпичей.
А если бы мы не стали группировать кирпичи на десятки и единицы, то можно было бы сказать, что число 35 содержит тридцать пять единиц. Такая группировка тоже была бы допустимой:
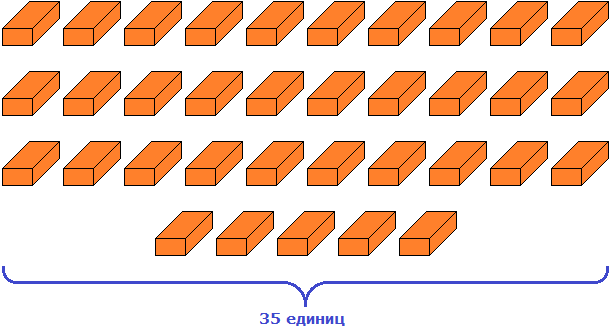
Аналогично можно рассуждать и про другие числа. К примеру, о числе 123. Ранее мы сказали, что это число содержит три единицы, два десятка и одну сотню. Но можно ещё сказать, что это число содержит 123 единицы. Более того, можно сгруппировать это число и другим образом, сказав что оно содержит 12 десятков и 3 единицы.
Слова единицы, десятки, сотни, заменяют собой множимые 1, 10 и 100. К примеру, в разряде единиц числа 123 располагается цифра 3. С помощью множимого 1 можно записать, что эта единица содержится в разряде единиц три раза:
1 × 3 = 3
Далее в разряде десятков числа 123 располагается цифра 2. С помощью множимого 10 можно записать, что эта десятка содержится в разряде десятков два раза:
10 × 2 = 20
Далее в разряде сотен числа 123 располагается цифра 1. С помощью множимого 100 можно записать, что эта сотня содержится в разряде сотен один раз:
100 × 1 = 100
Если сложить полученные результаты 3, 20 и 100, то получим число 123
3 + 20 + 100 = 123
То же самое будет происходить если мы скажем, что число 123 содержит 12 десятков и 3 единицы. Другими словами, десятки будут сгруппированы 12 раз:
10 × 12 = 120
А единицы три раза:
1 × 3 = 3
Это можно понять на следующем примере. Если имеется 123 яблока, то можно сгруппировать первые 120 яблок 12 раз по 10 штук:
Получилось сто двадцать яблок. Но осталось еще три яблока. Их мы назовем как «три единицы»
Если сложить полученные результаты 120 и 3, снова получим число 123
120 + 3 = 123
Ещё можно сгруппировать 123 яблока на одну сотню, два десятка и три единицы.
Сгруппируем сотню:
Сгруппируем два десятка:
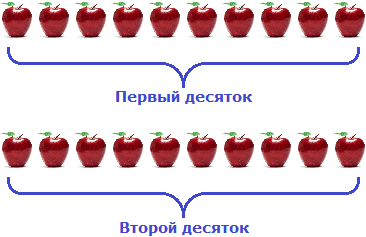
Сгруппируем три единицы:
Если сложить полученные результаты 100, 20 и 3, снова получим число 123
100 + 20 + 3 = 123
Ну и наконец, рассмотрим последнюю возможную группировку, где яблоки не будут распределяться на десятки и сотни, а будут собраны вместе. В таком случае число 123 будет читаться как «сто двадцать три единицы». Такая группировка тоже будет допустимой:
1 × 123 = 123
Пример 3. Прочитать число 523 всеми возможными способами.
Число 523 можно прочесть, как 3 единицы, 2 десятка и 5 сотен:
1 × 3 = 3 (три единицы)
10 × 2 = 20 (два десятка)
100 × 5 = 500 (пять сотен)
3 + 20 + 500 = 523
Ещё можно прочесть, как 3 единицы 52 десятка:
1 × 3 = 3 (три единицы)
10 × 52 = 520 (пятьдесят два десятка)
3 + 520 = 523
Ещё число 523 можно прочесть, как 523 единицы:
1 × 523 = 523 (пятьсот двадцать три единицы)
Где применить разряды?
Разряды существенно облегчают некоторые вычисления. Представьте, что вы у доски и решаете задачу. Вы почти закончили задачу, осталось только вычислить последнее выражение и получить ответ. Выражение, которое надо вычислить, выглядит следующим образом:
Калькулятора под рукой нет, а хочется быстро записать ответ и удивить всех скоростью своих вычислений. Всё просто, если отдельно сложить единицы, отдельно десятки и отдельно сотни. Начинать нужно с разряда единиц. В первую очередь после знака равно (=) необходимо мысленно поставить три точки. Вместо этих точек будет располагаться новое число (наш ответ):
Теперь начинаем складывать. В разряде единиц числа 632 располагается цифра 2, а в разряде единиц числа 264 — цифра 4. Это означает, разряд единиц числа 632 содержит две единицы, а разряд единиц числа 264 содержит четыре единицы. Складываем 2 и 4 единицы — получаем 6 единиц. Записываем цифру 6 в разряде единиц нового числа (нашего ответа):
Далее складываем десятки. В разряде десятков числа 632 располагается цифра 3, а в разряде десятков числа 264 — цифра 6. Это означает, что разряд десятков числа 632 содержит три десятка, а разряд десятков числа 264 содержит шесть десятков. Складываем 3 и 6 десятков — получаем 9 десятков. Записываем цифру 9 в разряде десятков нового числа (нашего ответа):
Ну и в завершении складываем отдельно сотни. В разряде сотен числа 632 располагается цифра 6, а в разряде сотен числа 264 — цифра 2. Это означает, что разряд сотен числа 632 содержит шесть сотен, а разряд сотен числа 264 содержит две сотни. Складываем 6 и 2 сотни, получаем 8 сотен. Записываем цифру 8 в разряде сотен нового числа (нашего ответа):
Таким образом, если к числу 632 прибавить 264, получается 896. Конечно, вы вычислите подобное выражение быстрее и окружающие начнут удивляться вашим способностям. Они будут думать, что вы быстро вычисляете большие числа, а на самом деле вы вычисляли маленькие. Согласитесь, что маленькие числа вычислять легче, чем большие.
Переполнение разряда
Разряд характеризуется одной цифрой от 0 до 9. Но иногда при вычислении числового выражения в середине решения может произойти переполнение разряда.
Например, при сложении чисел 32 и 14 переполнения не происходит. Сложение единиц этих чисел даст 6 единиц в новом числе. А сложение десятков этих чисел даст 4 десятка в новом числе. Получится ответ 46 или шесть единиц и четыре десятка.
А вот при сложении чисел 29 и 13 произойдёт переполнение. Сложение единиц этих чисел даёт 12 единиц, а сложение десятков 3 десятка. Если в новом числе в разряде единиц записать полученные 12 единиц, а в разряде десятков записать полученные 3 десятка, то получится ошибка:
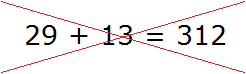
Значение выражения 29 + 13 равно 42, а не 312. Как же следует поступать при переполнении? В нашем случае переполнение случилось в разряде единиц нового числа. При сложении девяти и трёх единиц у нас получилось 12 единиц. А в разряд единиц можно записывать только цифры в диапазоне от 0 до 9.
Дело в том, что 12 единиц это не просто «двенадцать единиц». По другому это число можно прочитать как «две единицы и один десяток». Разряд единиц предназначен только для единиц. Десяткам там не место. Здесь и заключается наша ошибка. Сложив 9 единиц и 3 единицы мы получили 12 единиц, которые по-другому можно назвать двумя единицами и одним десятком. Записав две единицы и один десяток в одном разряде, мы допустили ошибку, которая в итоге привела к неправильному ответу.
Чтобы исправить ситуацию, две единицы нужно записать в разряде единиц нового числа, а оставшийся десяток перенести на следующий разряд десятков. После сложения десятков в примере 29 + 13, мы прибавим к полученному результату тот десяток, который остался при сложении единиц.
Итак, из 12 единиц две единицы запишем в разряде единиц нового числа, а один десяток перенесем на следующий разряд
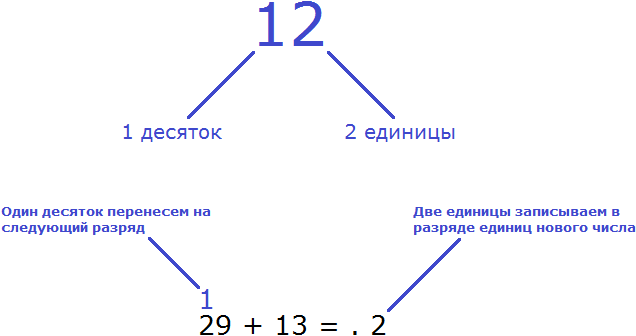
Как видно на рисунке, 12 единиц мы представили как 1 десяток и 2 единицы. Две единицы мы записали в разряде единиц нового числа. А один десяток перенесли к разрядам десятков. Этот десяток мы прибавим к результату сложения десятков чисел 29 и 13. Чтобы не забыть о нем, мы надписали его над десятками числа 29.
Теперь складываем десятки. Два десятка плюс один десяток будет три десятка, плюс один десяток, который остался от предыдущего сложения. В результате в разряде десятков получаем четыре десятка:
Пример 2. Сложить по разрядам числа 862 и 372.
Начинаем с разряда единиц. В разряде единиц числа 862 располагается цифра 2, в разряде единиц числа 372 — также цифра 2. Это означает, что разряд единиц числа 862 содержит две единицы, и разряд единиц числа 372 также содержит две единицы. Складываем 2 единицы плюс 2 единицы — получаем 4 единицы. Записываем цифру 4 в разряде единиц нового числа:
Далее складываем десятки. В разряде десятков числа 862 располагается цифра 6, а в разряде десятков числа 372 — число 7. Это означает, что разряд десятков числа 862 содержит шесть десятков, а разряд десятков числа 372 содержит семь десятков. Складываем 6 десятков и 7 десятков — получаем 13 десятков. Произошло переполнение разряда. 13 десятков это десятка повторенная 13 раз. А если повторить десятку 13 раз, то получится число 130
10 × 13 = 130
Число 130 состоит из трех десятков и одной сотни. Три десятка мы запишем в разряде десятков нового числа, а одну сотню отправим на следующий разряд:
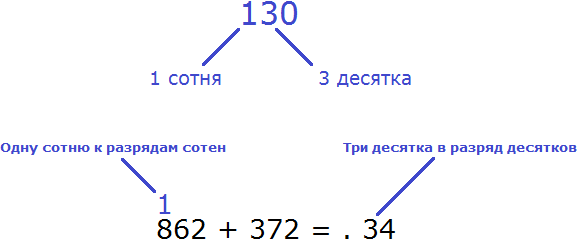
Как видно на рисунке, 13 десятков (число 130) мы представили как 1 сотню и 3 десятка. Три десятка мы записали в разряде десятков нового числа. А одну сотню перенесли к разрядам сотен. Эту сотню мы прибавим к результату сложения сотен чисел 862 и 372. Чтобы не забыть о ней, мы надписали её над сотнями числа 862.
Теперь складываем сотни. Восемь сотен плюс три сотни будет одиннадцать сотен плюс одна сотня, которая осталась от предыдущего сложения. В результате в разряде сотен получаем двенадцать сотен:
Здесь также происходит переполнение разряда сотен, но это не приводит к ошибке, поскольку решение завершено. При желании с 12 сотнями можно провести те же действия, что мы провели с 13 десятками.
12 сотен это сотня, повторенная 12 раз. А если повторить сотню 12 раз, то получится 1200
100 × 12 = 1200
В числе 1200 две сотни и одна тысяча. Две сотни записываются в разряд сотен нового числа, а одна тысяча перенеслась к разряду тысяч.
Теперь рассмотрим примеры на вычитание. Для начала вспомним, что такое вычитание. Это операция, которая позволяет от одного числа вычесть другое. Вычитание состоит из трёх параметров: уменьшаемого, вычитаемого и разности. Вычитать тоже нужно по разрядам.
Пример 3. Вычесть из числа 65 число 12.
Начинаем с разряда единиц. В разряде единиц числа 65 располагается цифра 5, а в разряде единиц числа 12 — цифра 2. Это означает, что разряд единиц числа 65 содержит пять единиц, а разряд единиц числа 12 содержит две единицы. Вычтем из пяти единиц две единицы, получим три единицы. Записываем цифру 3 в разряде единиц нового числа:
Теперь вычитаем десятки. В разряде десятков числа 65 располагается цифра 6, а в разряде десятков числа 12 — цифра 1. Это означает, что разряд десятков числа 65 содержит шесть десятков, а разряд десятков числа 12 содержит один десяток. Вычтем из шести десятков один десяток, получим пять десятков. Записываем цифру 5 в разряде десятков нового числа:
Пример 4. Вычесть из числа 32 число 15
В разряде единиц числа 32 содержится две единицы, а в разряде единиц числа 15 — пять единиц. От двух единиц не вычесть пять единиц, поскольку две единицы меньше, чем пять единиц.
Сгруппируем 32 яблока так, чтобы в первой группе было три десятка яблок, а во второй — оставшиеся две единицы яблок:
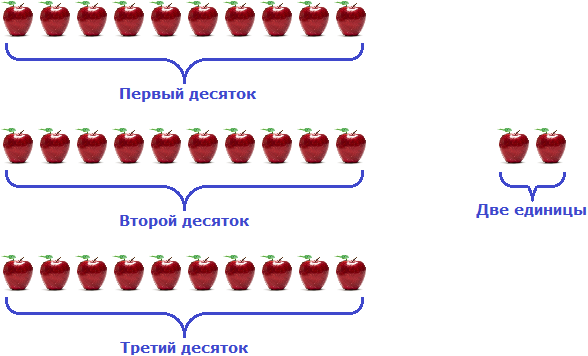
Итак, нам нужно из этих 32 яблок вычесть 15 яблок, то есть вычесть пять единиц и один десяток яблок. Причем вычесть по разрядам.
От двух единиц яблок нельзя вычесть пять единиц яблок. Чтобы выполнить вычитание, две единицы должны взять несколько яблок у соседней группы (разряда десятков). Но нельзя брать сколько хочется, поскольку десятки строго упорядочены по десять штук. Разряд десятков может дать двум единицам только один целый десяток.
Итак, берём один десяток из разряда десятков и отдаём его двум единицам:
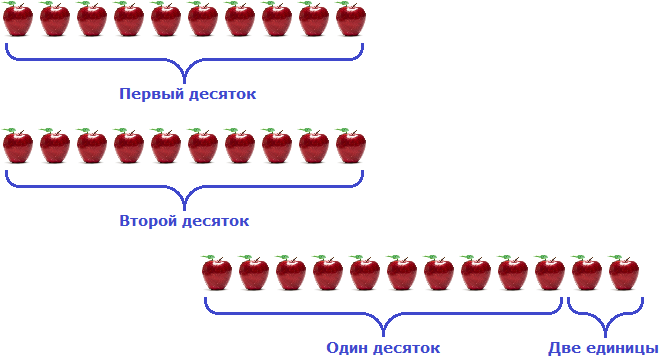
К двум единицам яблок теперь присоединился один десяток яблок. Получается 12 единиц яблок. А от двенадцати можно вычесть пять, получится семь. Записываем цифру 7 в разряде единиц нового числа:
Теперь вычитаем десятки. Поскольку разряд десятков отдал единицам один десяток, сейчас он имеет не три, а два десятка. Поэтому вычитаем из двух десятков один десяток. Останется один десяток. Записываем цифру 1 в разряде десятков нового числа:
Чтобы не забывать, что в каком-то разряде был взят один десяток (либо сотня либо тысяча), над этим разрядом принято ставить точку.
Пример 5. Вычесть из числа 653 число 286
В разряде единиц числа 653 содержится три единицы, а в разряде единиц числа 286 — шесть единиц. От трёх единиц не вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:
Взятый один десяток и три единицы вместе образуют тринадцать единиц. От тринадцати единиц можно вычесть шесть единиц, получится семь единиц. Записываем цифру 7 в разряде единиц нового числа:
Теперь вычитаем десятки. Раньше разряд десятков числа 653 содержал пять десятков, но мы взяли с него один десяток, и теперь в разряде десятков содержатся четыре десятка. Из четырех десятков не вычесть восемь десятков, поэтому берем одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню:
Взятая одна сотня и четыре десятка вместе образуют четырнадцать десятков. От четырнадцати десятков можно вычесть восемь десятков, получится шесть десятков. Записываем цифру 6 в разряде десятков нового числа:
Теперь вычитаем сотни. Раньше разряд сотен числа 653 содержал шесть сотен, но мы взяли с него одну сотню, и теперь в разряде сотен содержатся пять сотен. Из пяти сотен можно вычесть две сотни, получается три сотни. Записываем цифру 3 в разряде сотен нового числа:
Намного сложнее вычитать из чисел вида 100, 200, 300, 1000, 10000. То есть числа, у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда. Давайте посмотрим, как это происходит.
Пример 6. Вычесть из числа 200 число 84
В разряде единиц числа 200 содержится ноль единиц, а в разряде единиц числа 84 — четыре единицы. От нуля не вычесть четыре единицы, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:
Но в разряде десятков нет десятков, которые мы могли бы взять, поскольку там тоже ноль. Чтобы разряд десятков смог дать нам один десяток, мы должны взять для него одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню для разряда десятков:
Взятая одна сотня это десять десятков. От этих десяти десятков мы берём один десяток и отдаём его единицам. Этот взятый один десяток и прежние ноль единиц вместе образуют десять единиц. От десяти единиц можно вычесть четыре единицы, получится шесть единиц. Записываем цифру 6 в разряде единиц нового числа:
Теперь вычитаем десятки. Чтобы вычесть единицы мы обратились к разряду десятков за одним десятком, но на тот момент этот разряд был пуст. Чтобы разряд десятков смог дать нам один десяток, мы взяли одну сотню у разряда сотен. Эту одну сотню мы назвали «десять десятков». Один десяток мы отдали единицам. Значит на данный момент в разряде десятков содержатся не десять, а девять десятков. От девяти десятков можно вычесть восемь десятков, получится один десяток. Записываем цифру 1 в разряде десятков нового числа:
Теперь вычитаем сотни. Для разряда десятков мы брали у разряда сотен одну сотню. Значит сейчас в разряде сотен содержатся не две сотни, а одна. Поскольку в вычитаемом разряд сотен отсутствует, мы переносим эту одну сотню в разряд сотен нового числа:
Получили окончательный ответ 116.
Естественно, выполнять вычитание таким традиционным методом довольно сложно, особенно на первых порах. Поняв сам принцип вычитания, можно воспользоваться нестандартными способами.
Первый способ заключается в том, чтобы уменьшить число, у которого на конце нули на одну единицу. Далее из полученного результата вычесть вычитаемое и к полученной разности прибавить единицу, которую изначально вычли из уменьшаемого. Давайте решим предыдущий пример этим способом:
Уменьшаемое здесь это число 200. Уменьшим это число на единицу. Если от 200 вычесть 1 получится 199. Теперь в примере 200 − 84 вместо числа 200 записываем число 199 и решаем пример 199 − 84. А решение этого примера не составляет особого труда. Единицы вычтем из единиц, десятки из десятков, а сотню просто перенесем к новому числу, поскольку в числе 84 нет сотен:
Получили ответ 115. Теперь к этому ответу прибавляем единицу, которую мы изначально вычли из числа 200
Получили окончательный ответ 116.
Пример 7. Вычесть из числа 100000 число 91899
Вычтем из 100000 единицу, получим 99999
Теперь из 99999 вычитаем 91899
К полученному результату 8100 прибавим единицу, которую мы вычли из 100000
Получили окончательный ответ 8101.
Второй способ вычитания заключается в том, чтобы рассматривать цифру, находящуюся в разряде, как самостоятельное число. Решим несколько примеров этим способом.
Пример 8. Вычесть из числа 75 число 36
Будем считать, что каждая цифра в разряде это самостоятельное число.
Итак, в разряде единиц числа 75 располагается число 5, а в разряде единиц числа 36 располагается число 6. Из пяти не вычесть шести, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков.
В разряде десятков располагается число 7. Берем от этого числа одну единицу и мысленно дописываем её слева от числа 5
А поскольку от числа 7 взята одна единица, это число уменьшится на одну единицу и обратится в число 6
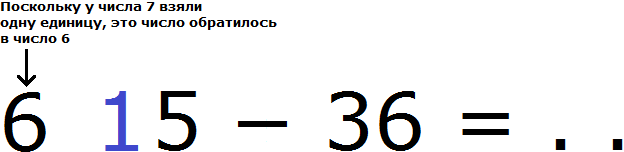
Теперь в разряде единиц числа 75 располагается число 15, а в разряде единиц числа 36 число 6. Из 15 можно вычесть 6, получится 9. Записываем число 9 в разряде единиц нового числа:
Переходим к следующему числу, находящемуся в разряде десятков. Раньше там располагалось число 7, но мы взяли с этого числа одну единицу, поэтому сейчас там располагается число 6. А в разряде десятков числа 36 располагается число 3. Из 6 можно вычесть 3, получится 3. Записываем число 3 в разряде десятков нового числа:
Пример 9. Вычесть из числа 200 число 84
Будем считать, что каждая цифра в разряде это самостоятельно число.
Итак, в разряде единиц числа 200 располагается ноль, а в разряде единиц числа 84 — располагается четыре. От нуля не вычесть четыре, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в разряде десятков тоже ноль. Ноль не сможет дать нам единицу. В таком случае за следующее принимаем число 20.
Берём одну единицу от числа 20 и мысленно дописываем её слева от нуля, располагающегося в разряде единиц. А поскольку от числа 20 взята одна единица, это число обратится в число 19
Теперь в разряде единиц располагается число 10. Десять минус четыре равно шесть. Записываем число 6 в разряде единиц нового числа:
Переходим к следующему числу, находящемуся в разряде десятков. Раньше там располагался ноль, но этот ноль вместе со следующей цифрой 2 образовал число 20, от которого мы брали одну единицу. В результате число 20 обратилось в число 19. Получается, что теперь в разряде десятков числа 200 располагается число 9, а в разряде десятков числа 84 располагается число 8. Девять минус восемь равно одному. Записываем число 1 в разряде десятков нашего ответа:
Переходим к следующему числу, находящемуся к разряду сотен. Раньше там располагалось число 2, но это число вместе с цифрой 0 мы приняли за число 20, от которого взяли одну единицу. В результате число 20 обратилось в число 19. Получается, что теперь в разряде сотен числа 200 располагается число 1, а в числе 84 разряд сотен пустой, поэтому мы переносим эту единицу к новому числу:
Этот метод поначалу кажется сложным и лишенным всякого смысла, но на деле он самый лёгкий. В основном мы будем им пользоваться при сложении и вычитании чисел в столбик.
Сложение в столбик
Сложение в столбик это школьная операция, которую помнят многие, но не мешает вспомнить её ещё раз. Сложение в столбик происходит по разрядам — единицы складываются с единицами, десятки с десятками, сотни с сотнями, тысячи с тысячами.
Рассмотрим несколько примеров.
Пример 1. Сложить 61 и 23.
Сначала записываем первое число, а под ним второе число так, чтобы единицы и десятки второго числа оказались под единицами и десятками первого числа. Всё это соединяем знаком сложения (+) по вертикали:
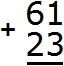
Теперь единицы первого числа складываем с единицами второго числа, а десятки первого числа складываем с десятками второго числа:
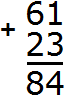
Получили 61 + 23 = 84.
Пример 2. Сложить 108 и 60
Записываем числа в столбик. Единицы под единицами, десятки под десятками:
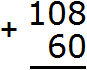
Теперь складываем единицы первого числа с единицами второго числа, десятки первого числа с десятками второго числа, сотни первого числа с сотнями второго числа. Но сотня есть только у первого числа 108. В этом случае цифра 1 из разряда сотен добавляется к новому числу (нашему ответу). Как говорили в школе «сносится»:
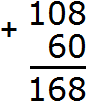
Видно, что мы снесли цифру 1 к нашему ответу.
Когда речь идёт о сложении, нет разницы в каком порядке записывать числа. Наш пример вполне можно было записать и так:
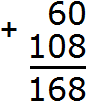
Первая запись, где число 108 было наверху, более удобнее для вычисления. Человек вправе выбирать любую запись, но обязательно нужно помнить, что единицы надо записывать строго под единицами, десятки под десятками, сотни под сотнями. Другими словами, следующие записи будут неправильными:
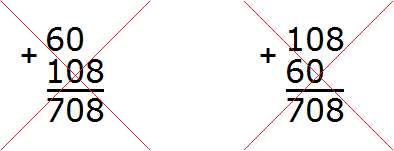
Если вдруг при сложении соответствующих разрядов получится число, которое не помещается в разряд нового числа, то необходимо записать одну цифру из младшего разряда, а оставшуюся перенести на следующий разряд.
Речь в данном случае идет о переполнении разряда, о котором мы говорили ранее. Например, при сложении 26 и 98 получается 124. Давайте посмотрим, как это получилось.
Записываем числа в столбик. Единицы под единицами, десятки под десятками:
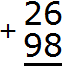
Складываем единицы первого числа с единицами второго числа: 6+8=14. Получили число 14, которое не вместится в разряд единиц нашего ответа. В таких случаях мы сначала вытаскиваем из 14 цифру, находящуюся в разряде единиц и записываем её в разряде единиц нашего ответа. В разряде единиц числа 14 располагается цифра 4. Записываем эту цифру в разряде единиц нашего ответа:
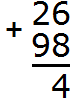А куда девать цифру 1 из числа 14? Здесь начинается самое интересное. Эту единицу мы переносим на следующий разряд. Она будет добавлена к разряду десятков нашего ответа.
Складываем десятки с десятками. 2 плюс 9 равно 11, плюс добавляем единицу, которая досталась нам от числа 14. Добавив к 11 нашу единицу, мы получим число 12, которое и запишем в разряде десятков нашего ответа. Поскольку это конец решения, здесь уже не стоит вопрос о том, вместится ли полученный ответ в разряд десятков. 12 мы записываем целиком, образуя окончательный ответ.
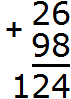
Получили ответ 124.
Говоря традиционным методом сложения, при сложении 6 и 8 единиц получилось 14 единиц. 14 единиц это 4 единицы и 1 десяток. Четыре единицы мы записали в разряде единиц, а один десяток отправили на следующий разряд (к разрядам десятков). Затем сложив 2 десятка и 9 десятков, мы получили 11 десятков, плюс добавили 1 десяток, который остался при сложении единиц. В результате получили 12 десятков. Эти двенадцать десятков мы записали целиком, образуя окончательный ответ 124.
Этот простенький пример демонстрирует школьную ситуацию, в которой говорят «четыре пишем, один в уме». Если вы будете решать примеры и у вас после сложения разрядов останется цифра, которую надо держать в уме, запишите её над тем разрядом, куда она будет потом добавлена. Это позволит вам не забыть о ней:
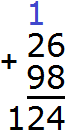
Пример 2. Сложить числа 784 и 548
Записываем числа в столбик. Единицы под единицами, десятки под десятками, сотни под сотнями:
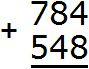
Складываем единицы первого числа с единицами второго числа: 4+8=12. Число 12 не вмещается в разряд единиц нашего ответа, поэтому мы из 12 вынимаем цифру 2 из разряда единиц и записываем её в разряд единиц нашего ответа. А цифру 1 переносим на следующий разряд:
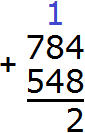
Теперь складываем десятки. Складываем 8 и 4 плюс единица, которая осталась от предыдущей операции (единица осталась от 12, на рисунке она выделена синим цветом). Складываем 8+4+1=13. Число 13 не вместится в разряд десятков нашего ответа, поэтому мы запишем цифру 3 в разряде десятков, а единицу перенесём на следующий разряд:
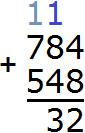
Теперь складываем сотни. Складываем 7 и 5 плюс единица, которая осталась от предыдущей операции: 7+5+1=13. Записываем число 13 в разряд сотен:
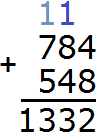
Вычитание в столбик
Пример 1. Вычтем из числа 69 число 53.
Запишем числа в столбик. Единицы под единицами, десятки под десятками. Затем вычитаем по разрядам. Из единиц первого числа вычитаем единицы второго числа. Из десятков первого числа вычитаем десятки второго числа:
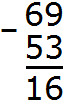
Получили ответ 16.
Пример 2. Найти значение выражения 95 − 26
Записываем в столбик данное выражение:
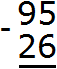
Разряд единиц числа 95 содержит 5 единиц, а разряд единиц числа 26 содержит 6 единиц. От пяти единиц нельзя вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Этот десяток и имеющиеся пять единиц вместе составляют 15 единиц. Из 15 единиц можно вычесть 6 единиц, получится 9 единиц. Записываем цифру 9 в разряде единиц нашего ответа:
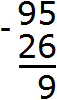
Теперь вычитаем десятки. Разряд десятков числа 95 раньше содержал 9 десятков, но мы взяли с этого разряда один десяток, и сейчас он содержит 8 десятков. А разряд десятков числа 26 содержит 2 десятка. Из восьми десятков можно вычесть два десятка, получится шесть десятков. Записываем цифру 6 в разряде десятков нашего ответа:
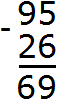
Воспользуемся нестандартным способом вычитания при котором каждая цифра, входящая в число, рассматривается как отдельное число. При вычитании больших чисел в столбик этот способ очень удобен.
В разряде единиц уменьшаемого располагается число 5. А в разряде единиц вычитаемого число 6. Из пятёрки не вычесть шестёрку. Поэтому берем одну единицу у числа 9. Взятая единица мысленно дописывается слева от пятёрки. А поскольку у числа 9 мы взяли одну единицу, это число уменьшится на одну единицу:
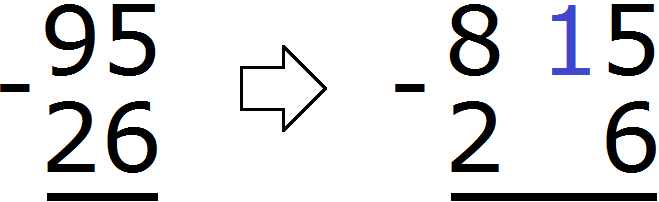
В результате пятёрка обращается в число 15. Теперь можно из 15 вычесть 6. Получается 9. Записываем число 9 в разряде единиц нашего ответа:
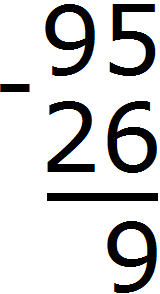
Переходим к разряду десятков. Раньше там располагалось число 9, но поскольку мы взяли у него одну единицу оно обратилось в число 8. В разряде десятков второго числа располагается число 2. Восемь минус два будет шесть. Записываем число 6 в разряде десятков нашего ответа:
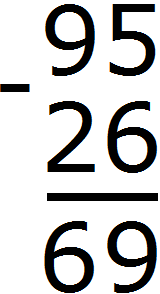
Пример 3. Найдем значение выражения 2412 − 2317
Записываем в столбик данное выражение:
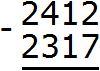
В разряде единиц числа 2412 располагается число 2, а в разряде единиц числа 2317 располагается число 7. Из двойки не вычесть семёрку, поэтому берем единицу у следующего числа 1. Взятую единицу мысленно дописываем слева от двойки:
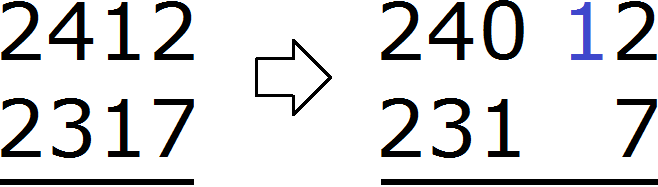
В результате двойка обращается в число 12. Теперь можно из 12 вычесть 7. Получается 5. Записываем цифру 5 в разряде единиц нашего ответа:
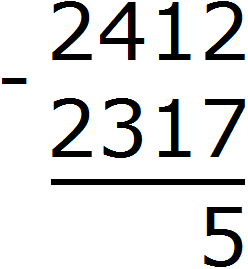
Переходим к десяткам. В разряде десятков числа 2412 раньше располагалось число 1, но поскольку мы взяли у него одну единицу, оно обратилось в 0. А в разряде десятков числа 2317 располагается число 1. Из нуля не вычесть единицу. Поэтому берем одну единицу у следующего числа 4. Взятую единицу мысленно дописываем слева от нуля. А поскольку у числа 4 мы взяли одну единицу, это число уменьшится на одну единицу:
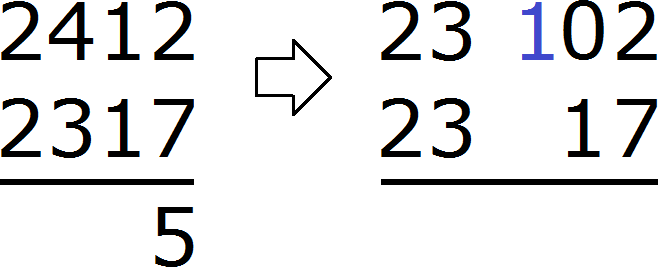
В результате ноль обращается в число 10. Теперь можно из 10 вычесть 1. Получается 9. Записываем цифру 9 в разряде десятков нашего ответа:
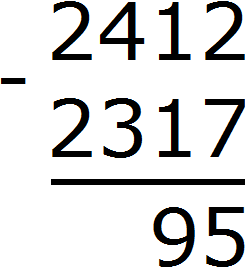
В разряде сотен числа 2412 раньше располагалось число 4, но сейчас там располагается число 3. В разряде сотен числа 2317 также располагается число 3. Три минус три равно нулю. То же самое и с разрядами тысяч в обоих числах. Два минус два равно нулю. А если разность старших разрядов равна нулю, то этот ноль не записывают. Поэтому окончательным ответом будет число 95.
Пример 4. Найти значение выражения 600 − 8
Запишем в столбик данное выражение:
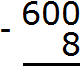
В разряде единиц числа 600 располагается ноль, а в разряде единиц числа 8 само это число. Из нуля не вычесть восьмерку, поэтому берем единицу у следующего числа. Но следующее число это тоже ноль. Тогда за следующее число принимаем число 60. Берем одну единицу у этого числа и мысленно дописываем её слева от нуля. А поскольку у числа 60 мы взяли одну единицу, это число уменьшится на одну единицу:
Теперь в разряде единиц располагается число 10. Из 10 можно вычесть 8, получится 2. Записываем число 2 в разряде единиц нового числа:
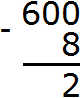
Переходим к следующему числу, находящемуся в разряде десятков. В разряде десятков раньше располагался ноль, но сейчас там располагается число 9, а во втором числе разряд десятков отсутствует. Поэтому число 9 переносится к новому числу:
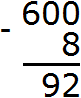
Переходим к следующему числу, находящемуся в разряде сотен. В разряде сотен раньше располагалось число 6, но сейчас там располагается число 5, а во втором числе разряд сотен отсутствует. Поэтому число 5 переносится к новому числу:
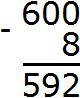
Пример 5. Найти значение выражения 10000 − 999
Запишем в столбик данное выражение:
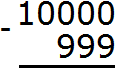
В разряде единиц числа 10000 располагается 0, а в разряде единиц числа 999 располагается число 9. Из нуля не вычесть девятку, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в следующем разряде тоже ноль. Тогда за следующее число принимаем 1000 и берем от этого числа единицу:
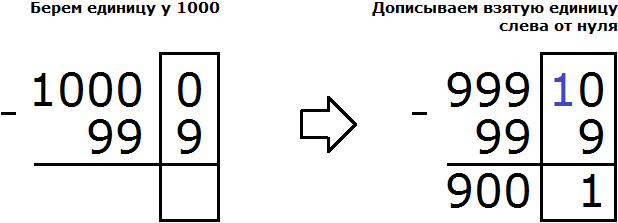
Следующее число в данном случае было 1000. Взяв у него единицу, мы обратили его в число 999. А взятую единицу дописали слева от нуля.
Дальнейшее вычисление не составило особого труда. Десять минус девять равно одному. Вычитание чисел, находящихся в разряде десятков обоих чисел дало ноль. Вычитание чисел, находящихся в разряде сотен обоих чисел тоже дало ноль. А девятка из разряда тысяч была перенесена к новому числу:
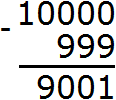
Пример 6. Найти значение выражения 12301 − 9046
Запишем в столбик данное выражение:
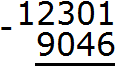
В разряде единиц числа 12301 располагается число 1, а в разряде единиц числа 9046 располагается число 6. Из единицы не вычесть шесть, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в следующем разряде располагается ноль. Ноль ничего нам дать не сможет. Тогда за следующее число принимаем 1230 и берем от этого числа единицу:
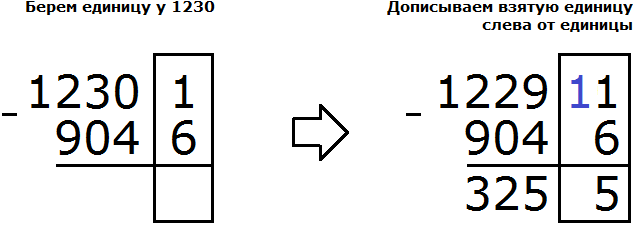
Следующее число в данном случае было 1230. Взяв у него единицу, мы обратили его в число 1229. А взятую единицу мысленно дописали слева от единицы, находящейся в разряде единиц.
Дальнейшее вычисление не составило особого труда. Одиннадцать минус шесть равно пять. Вычитание чисел, находящихся в разряде десятков обоих чисел дало число 5. Вычитание чисел, находящихся в разряде сотен обоих чисел дало число 2. Вычитание чисел, находящихся в разряде тысяч обоих чисел дало число 3.
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
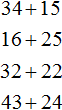
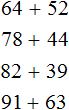
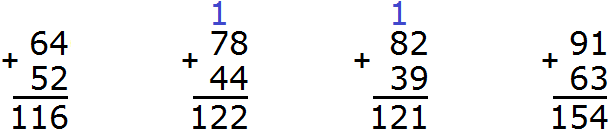
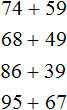
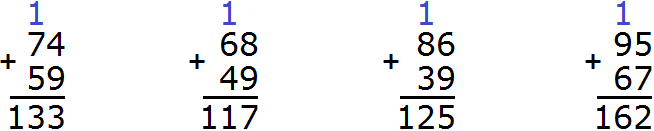
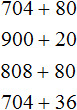
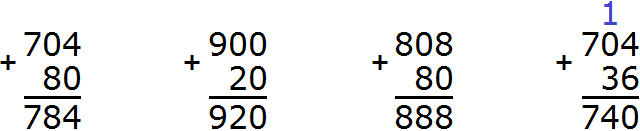
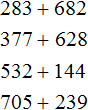
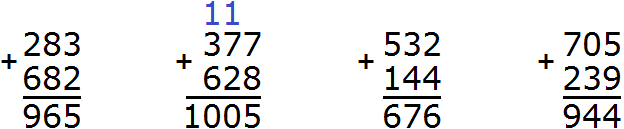
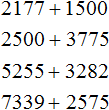
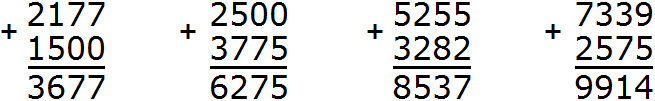
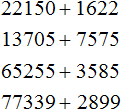
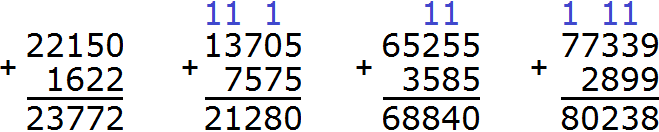
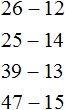
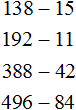
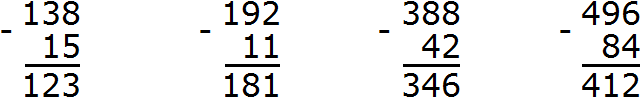
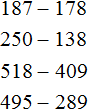
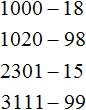
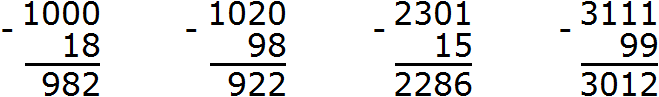
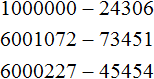
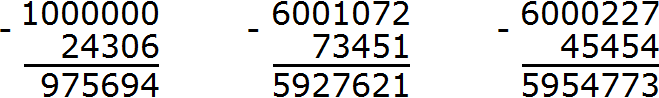
До этого урока уже многие не дошли )
Дошёл. Завершил.
Молодец!
Я дошел до этого урока. Но он был самый сложный и запарный. Но в итоге я все выучил. Теперь умею решать все это дело. Хотя это и заняло на пару часов больше чем прошлые уроки.)
я 3 часа учил
я смог дойти готовлюсь к ОГЭ
+++
Четко и понятно. Респект админу
Большое спасибо вам за знания, что вы даёте!
очень доступно , без лишней воды . Спасибо
Без лишней воды? Whaaaat?….
Много пить вредно.
Я напишу только один комментарий на этом сайте. Администратору всего самого наилучшего ! Круто сделал, все четко, ясно и понятно.
Минус.
Я бы этот сайт начал бы с элементов линейной алегебы и Евклидовой геометрии. После рассказывал бы уже тригонометрию и высшие элементы, где на такие простые вещи просто не обращаешь внимание. Если в 21 веке обычные люди не знают первые 30 статей этого сайта. То это очень печально и очень грустно что на столь не развита логика и мышление у людей, что даже элементарные вещи которые еще наверно в садике и в первом классе рассказывают. Стоило бы задуматься, куда катиться наш мир, а тем более куда катиться наше будущее поколение которое не может построить элементарный график показателя погоды и рассчитать примерный процент.
Огромное спасибо автору сайта за то что рассказывает вам то что вам уже рассказывали 100500 раз !!!
Ну а если я скажу тебе что с логикой и анализом у меня все более чем в порядке, более того — я композитор, и что я просто забивал на математику все школьные годы? Ибо она мне даже сейчас пригодится только для программирования. Я теперь от этого тупой, деградант, плохое поколение?
О, ещё один композитор, обнулившийся в математике, на которую забивал, для чего-то другого. Мне для физики.
Вы, будьте добры, не судите, да не будете судимы. Ведь не так уж страшно, что Вы не знаете о том, что в Вашем предложении: Стоило бы задуматься, куда катиться наш мир, а тем более куда катиться наше будущее поколение… — катиТСя — пишется без мягкого знака, из-за которого Ваш комментарий воспринимается уже, как пустой претенциозный фарс, и его содержание перестаёт быть интересным.
Вы, будьте добры, не судите, да не будете судимы. Ведь не так уж страшно, что Вы не знаете о том, что в Вашем предложении: Стоило бы задуматься, куда катиться наш мир, а тем более куда катиться наше будущее поколение… — катиТСя — пишется без мягкого знака, из-за которого Ваш комментарий воспринимается уже, как пустой претенциозный фарс, и его содержание перестаёт быть интересным.
Уважаемый аноним, вы очень не правы)) Да, первые уроки очень просты, но даже я узнала что то новое из них) Эти уроки закладывают математическую логику (у меня ее нет вообще)))), например я знаю как считать в столбик, но почему именно так я не знаю, а тут именно объяснено что, как и почему. Это иногда как в русском языке (к примеру), ты знаешь как правильно писать слово потому что вызубрил-выучил его, но не знаешь почему оно пишется именно так, потому что не знаешь правила)
Админу спасибо за уроки! Все доступно и понятно! Если бы еще были такие же по биологии/химии/физики то было бы просто замечательно 🙂
Я согласна. В классе мне иногда не объясняли такие вещи даже если я спрашивала. Говорили мол «просто делай так и всё».
Ну госпожа Мария, на то вы и Мария а не Хендрик Лоренц или Макс Планк. И то что вы русский просто взубрили тоже не есть хорошо. А я сюда пришёл выучить математику необходимую для понимания физики, в частности астрофизики. Пришёл и ничего не нашёл(
Я это все знала,но нужно вспомнить,так как мозги особо не напрягала, ведь есть же калькулятор)))
Ну как видишь люди интересуются математикой раз на сайте так много комментариев. Проблема не в людях, а в системе образования которая не способна зародить интерес у людей к науке .
Не стану спорить,первые статьи реально детские. С другой стороны,если математику решит изучать ребенок,то это в самый раз. И,в добавок,в более сознательном возрасте каждый может пересмотреть свой взгляд на элементарную математику. Например,я начал понимать,какого это — мыслить математически. В математике мы всегда задаём себе ЦЕЛЬ(Вычислить х-2=4),потом определяем,какие условия есть у этой цели(Мы не знаем Х),и выбираем инструменты для решения этой цели(Формулы). Звучит элементарно,но дело в том,что такие вот «цели,инструменты,условия» есть у всех проблем в нашей жизни:) даже у самых сложных и запутанных. Очень простая мысль,но спроси меня раньше,»по какому порядку решаются проблемы»(Цель,определение условий,поиск формул/создание формулы),то четкого ответа я бы не смог дать. Да и банальные тезисы повторить тоже полезно…
Доброго дня, Аноним) про «катится мир»: разница между Вами и автором, что он создал этот ресурс, где я могу начать всё заново, а Вы со своей линейной алгеброй и тригонометрией — нет.
Спасибо.
Спасибо большое автору за возможность!
На ресурсе, где девиз «математика с нуля», написать такой комментарий — это просто сверх разумом нужно быть.
ХАХАХАХАХАХХАХАХАХАХАХАХАХ
РЕАЛЬНО НАПИСАТЬ ТАКОЙ КОММЕНТАРИЙ ПОД ДЕВИЗОМ »МАТЕМАТИКА С НУЛЯ» ЭТО КАК-ТО ******) СВЕРХ—РАЗУМ)) АЛЕКСАНДР БРОО УВАЖАЮ И ЦЕНЮ ТО ЧТО ТЫ СДЕЛАЛ ДЛЯ ЭТОГО САЙТА КАК И МНОГИЕ ПОЗИТИВНЫЕ АДЕКВАТНЫЕ ЛЮДИ ( НЕ СМОТРИ НА КОММЕНТЫ НЕ БЛАГОДАРНЫЕ !! СПАСИБО ЗА ТРУД ! РЕСПЕКТ
знаете эти статьи нужны например для того чтобы в 25-30 лет подготовить ребенка к школе или чтобы он сам мог выучить некоторые темы зарание
Чувак, ну я не знаю первые тридцать статей этого курса. Если ты такой шибко умный, то найди себе другие учебники или ресурсы и учись с «с элементов линейной алегебы и Евклидовой геометрии». Этот курс явно не для тебя.
Я работаю и учусь по этому курсу. А в школе я был намного тупее, чем ныне.
А так вообще ты можешь написать свой курс «для особо одарённых.
Ну а если погасить возмущение и не кидаться в крайности, то могу сказать что в интернете очень мало ресурсов, собирающих в себе всю информацию, от начала до конца.
Не зная, что искать, извиняюсь, хер найдёшь.
Ну раз Вам автор, ув. Аноним, ничего нового не рассказал, то будьте добры, найдите какой-нибудь форум, где и пойте песни в стиле «куда катиться наш мир», и не нужно никому понижать самооценку, и никого «опускать». У всех были свои причины, чтобы сюда прийти.
Здравствуйте! =)
Большое Вам спасибо
У меня возникли трудности с решением примеров как в 12 задании =( Мы рассматривали более простые числа в уроке
Пожалуйста, можете объяснить также детально решение семизначных чисел с нулями в столбик
Привет.
От нуля не вычесть шесть, поэтому занимаешь единицу у соседнего числа 100000 и мысленно дописываешь эту единицу слева от нуля из которого хочешь вычесть 6. А 100000 обращается в число 99999, потому что была занята одна единица. Дальше вычитание происходит как обычно.
А так, тема довольно сложная не только для освоения, но и для объяснения. Советую очень внимательно прочитать подраздел Переполнение разряда, выполняя в тетради все описанные шаги.
Большое спасибо! =)
Здравствуйте еще раз 😀
Сидела-сидела, вроде, поняла Ваше объяснение
Но!
Допустим вычитаем из 2000000 число 75333
Занимаем же в итоге десяток, почему от 200 000 остается 199 999, а не 199 990 ?
Привет.
Это нестандартный метод вычитания 🙂 Не путайте его с традиционным.
От 200 000 вы занимаем не 10, а 1 и дописываем эту единицу слева от нуля, тем самым обращая этот ноль в число 10. А 200 000 обращается в число 199 999.
Если же вы пользуетесь обычным методом, как в школе, то сначала пытайтесь занять десяток, если его нет, то сотню для десятка. Если и сотни нет, то занимаете тысячу для сотни и так далее, пока не будет выполнено вычитание в младшем разряде.
Изучите раздел группировка предметов и переполнение разряда. Должно стать понятным 😉
А если на месте 2000000, поставить 2000200. Как тогда будет правильно объяснить тот же пример.
Точно так же. Вычитаем единицы. Разряд единиц пуст. Берем десяток от разряда десятков. Но разряд десятков тоже пуст. Тогда берем сотню для разряда десятков. Взяв сотню для разряда десятков, один десяток от этой сотни отправляем в разряд единиц, а девять десятков оставляем в разряде десятков.
Теперь вычитаем единицы 10-3=7
Вычитам десятки 9-3=6
Вычитаем сотни, но там теперь не две, а одна сотня, поскольку у нее занимали одну сотню. Занимаем тысячу у разряда тысяч, но разряд тысяч пуст. Тогда занимаем десяток тысяч для разряда тысяч, но разряд десятков тысяч тоже пуст. Тогда занимаем сотню тысяч, для разряда десятков тысяч, но разряд сотен тысяч тоже пуст. Тогда занимаем миллион для сотен тысяч. Взяв миллион, девять сотен тысяч оставляем в разряде сотен тысяч, а одну сотню тысяч отправляем в разряд десятков тысяч. В разряде десятков тысяч оставляем девять десятков тысяч, а один десяток тысяч отправляем в разряд тысяч. В разряде тысяч оставляем девять тысяч, а одну тысячу отправляем в разряд сотен. Теперь в разряде сотен одна сотня плюс десять сотен, которые взяли от разряда тысяч, итого 11 сотен
Далее вычитаем тысячи. Теперь там девять тысяч, поскольку была занята одна тысяча для разряда сотен
Далее вычитаем десятки тысяч. Теперь там девять десятков тысяч, поскольку был занят один десяток тысяч для разряда тысяч
Далее сносим сотни и миллионы:
Ну или вообще попроще:
Спасибо большое! Я понимаю Ваше объяснение.
Я не понимаю, как традиционным методом произвести вычитание 2 000 000 и 75 333
К примеру, Ваш пример 200-84 я понимаю, что там 10 десятков от одной сотни
Но я не понимаю, как раскладывается 2 000 000
Извините!
с 2 убираешь один у тебя из 2 000 000 превращается 1 999 99/10 и теперь спокойно отнимаешь 75 333 ответ 1925667
Ответ 1924667
. . . . . .
из 2 000 000 яблок забираем 75 333
Вы занимаете из 7 разряда(миллионов) 1 миллион яблок в 6 разряд (сотни тысяч) получается что у нас в 6 разряде 100 000 раз по 10 яблок.
Далее из 6 разряда(сотни тысяч) мы берем в 5 разряд (десятки тысяч) 100 000 яблок, получается что в 5 разряде у нас 10 000 раз по 10 яблок.
Далее из 5 разряда(десятки тысяч) мы берем в 4 разряд(тысячи) 10 000 яблок значит в разряде 4 у нас 1000 раз по 10 яблок.
Далее из 4 разряда(тысячи) мы берем в 3 разряд(сотни) 1 000 яблок значит в разряде 3 у нас 100 раз по 10 яблок.
Далее из 3 разряда(сотни) мы берем во 2 разряд(десятки) 100 яблок значит в разряде 2 у нас 10 раз по 10 яблок.
Далее из 2 разряда(десятки) мы берем в 1 разряд(единицы) 10 яблок значит в 1 разряде у нас 1 раз по 10 яблок
итого получается что заняв на каждый разряд яблоки выходит такая сумма 1 999 99(10 единиц) — 75 333, вычитаем единицы получается 1 999 997 — 75 330, дальше я думаю понятно. Традиционно решать такое мазохизм конечно.
Медленно но верно, дорога к сопромату. Пожелайте мне удачи друзья
Привет
Когда я впервые зашол на сайт я нечего не понимал но сейчас я решил 12 заданий в уме и мне 16 … из Кыргызстана.
Спасибо админу☺☺
Здравствуйте! скажите почему нельзя группировать 523 как 5 сотен и 23 единицы?
Здравствуйте.
Можно.
Все очень даже годно, единственное заданий для само-проверки побольше бы, и вообще перфек)
Очень внятное объяснение!
Спасибо за Ваш труд!
Спасибо огромное! всем тем кто придумал это все,это намного легче и понятливее чем в школе,хотя в школе то я не учился )) с большой радостью,обучаюсь у вас! Вы супер
Спасибо Вам огромное!
Я на этом сайте разбираю математику со своим ребёнком, к сожалению в школе учитель математики не утруждает себя что-то объяснять ребёнку, а тут всё понятно, доступно. Отличный сайт! Комментарий про деградацию поколения был лишний, так как человек, писавший комментарий, сам тут оказался, наверное, непросто так.
Админ ты красавчик зашел на твой сайт по совету канала в youtube «Хауди Хо» я изучаю программирование поэтому надо развить логику математика единственный предмет который хорошо повышает ее. Спасибо тебе Админ.
Полезно считать, что не считать не полезно.
Не пойму, в пункте про вычитание указаны кроме традиционного способа еще два дополнительных. В одном говорится про вычитание из уменьшаемого единицы, а во втором способе про представление цифр как чисел. Но этот второй способ вообще ничем не отличается на практике от традиционного, они абсолютно идентичны. Зачем он тогда нужен, только путаница возникает.
И еще подскажите, как столбиком вычесть из 333 999? У меня не получается 666 вообще никаким способом.
Точно так же. Но чтобы из меньшего числа вычесть бОльшее, нужно из бОльшего вычесть меньшее, и перед полученным ответом поставить минус.
Поэтому сначала решаете пример 999-333
и перед ответом 666 ставите минус
333 — 999 = -666
Метод столбиком работает тогда, когда уменьшаемое больше вычитаемого.
Все очень доступно для понимания!
И в конце отличные примеры для закрепления!!!
Все решил правильно!
Спасибо авторам, идем дальше!
Нигде не встречал настолько подробных разъяснений!
Автору огромное спасибо за такой труд. После таких уроков все становится понятно, Математика перестает быть чем то страшным и непонятным. Отдельное спасибо за столь простое и лаконичное оформление сайта, ничто не отвлекает от основного материала. Все так же красиво и гармонично, как и в самой математике )
Спасибо большое за сайт,очень помогает.
Все знать не будешь).
que jenial …que Dios les bendiga mucho.. muchas gracias les amo mucho …Mando saludos desde Argentina ..Abrazos hermanos Rusos ..
моя жена в математике просто супер.Она решает задачи как по маслу. А вот я разговариваю на 5 языках а она учен затрудняется даже на одном .Так что …авторам сайта огромное спосибо и большой поклон .. а всезнайкам советую одуматься ..Есть и жизненная математика в котором многие не тянут даже на двойку …а эта математика труднее даже квантовой ….так что callate tu
Как делать 109678×458
Подробнее в Умножение
Спасибо! Всё очень доступно и детально изложено.
Решил посчитать в уме. Не так просто сосчитать все что имеет больше 3 разрядов.
Спасибо большое
Спасибо за подробное разъяснение, этого очень не хватало, так как раньше просто говорили это делается так и так, а почему именно так, никто не говорил. Не было понимания процесса действий. Желаю вам развития проекта и создания новых в точных науках. Кому не хватает задач для решения, вот сайт https://uchik.ru (не реклама), очень удобно, каждый раз генерит новые задания, можно распечатать, я так и делаю.
Уважаемый Автор проета! Огромное СПАСИБО за проделанную работу!!! Предельно просто,ясно и интересно.
Один вопрос-несколько лет назад впервые нашла Ваш сайт, когда искала способ обьяснить на примерах моему сыну действия с дробями.И в тот момент сайт имел traductor на испанский.(Живу в Аргентине,дети не владеют русским…) И мой сын осилил тему без усилий и потом несколько раз самостоятьно искал нужную тему на Вашем сайте.Очень успешно!
Сейчас хотела»открыть»математику для младшей дочери и не смогла найти»переводчик».Может быть я плохо ищу,помогите пожалуйста! Еще раз Огромное Спасибо за Ваш труд!
Здравствуйте. Спасибо и Вам.
Сайт не имеет перевода на испанский язык.
Некоторые браузеры делают перевод автоматически. Возможно в прошлый раз вы пользовались таким браузером, и он вам перевёл страницы автоматом.
Если ваш браузер Google Chrome, найдите в правом верхнем углу браузера значок
и нажмите на него, сайт будет переведён автоматически.
Здравствуйте !
Как связаться с автором для обсуждения вопросов о сотрудничестве ?
Здравствуйте. Предложения по сотрудничеству временно не рассматриваются.
Привет Админ Я Из Узбекистан Я не очень хорошо знаю русский язык ну Серовно все понятно мне спасибо за все Я учусь В Университет дажи в университете наш пропадавател не абиснеяет как тебе ты супер 998911100611
ozodvaijonov564@gmail.com
Уххху. Прочитал весь урок, хоть все это знал,но не помешало повторить. Но после листая от начала до конца был в шоке, как мне не надоело столько читать известной мне информации? Админу огромная благодарность за твой труд, и пусть Бог тебя благословит в ещё большем успехе за то , что ты сделал такой удобный ,понятный, по полочкам разложенный урок. Такой вариант как раз многим не хватает,не все люди быстро и хорошо соображают,каждому дан свой талант , но этот сайт выручает таких людей.
Объясните плиз что значат следующие слова:
«В случае группировки предметов, разряды можно читать слева направо. Так, цифра 3 в числе 35 будет говорить о том, что в числе 35 содержатся три десятка. А это значит, что 35 кирпичей можно сгруппировать три раза по десять штук.»
Ничего не понял, учитывая что всё с легкостью понимал именно до этих строк.
Число 35 содержит пять единиц и три десятка (или три десятка и пять единиц).
Аналогия с кирпичами была введена для наглядности. Думали, что людям проще будет понимать, если приводить в пример реальное число каких-нибудь предметов.
«В случае группировки предметов, разряды можно читать слева направо. Так, цифра 3 в числе 35 будет говорить о том, что в числе 35 содержатся три десятка. А это значит, что 35 кирпичей можно сгруппировать три раза по десять штук.»
Удобно сначала сложить кирпичики по три десятка, а потом доложить еще пять штук.
Vielen Dank!
Нетрадиционный метод вычитания, как по мне, какой-то загонный. Мне кажется, он полезен только для начинающих, чтобы более наглядно принцип понять. А вот фишка с вычитанием единицы из числа с нулями (1000-55=999-55+1) удобная, не помню, чтобы нам про это в школе рассказывали 🙂
Вы не правы, нестандартный метод проще и быстрее всего — если его понять, конечно. Технически он прост, а причины его работы лежат в самой сути десятичной системы исчисления — десять единиц одного разряда образуют одну единицу старшего разряда . По сути это то же самое разложение числа на группы, но методически более удобное для целей вычисления . Способ же с единицей может и неплох, но он во—первых, слишком узкоспециализированн, так как может быть применим только для чисел; содержащих одни нули кроме самого старшего разряда ( для числа 20101 что вам даст этот способ?), а во—вторых, нетрадиционный способ все равно будет гораздо быстрее, так как не будет лишних действий при решении примера.
Отличный сайт! Всё структурировано, чётко и понятно. Задания для самостоятельной тренировки — также замечательные, но есть 1 единственный минус (или пожелание): дело в том, что сайтом хотят воспользоваться люди с ограниченными возможностями — по зрению, в том числе, и все они (задания), непосредственно, до данной темы были доступны, а здесь уже, судя по-всему, представлены в формате картинки и, с помощью программ экранного доступа (далее, озвучивающих) не прочитываются вовсе. Не сочтите за критику — всего лишь пожелание к улучшению. С большим удовольствием продолжила бы заниматься на данном сайте, если бы информация стала более доступной. Спасибо за внимание.
Спасибо большое за урок. Решил вот, программистом попробовать стать. Начать решил с азов. С математики 🙂 На вычитание с нулями чутка буксанул, но в итоге освоил. Надеюсь и дальше все пойдет)
Привет.
Спасибо за объяснения! Немного запутался.
Решаю пример:
69 — 53 = 16 — все верно
Решаю пример столбиком (69 — 53)
69
53
—-
16 — тоже все верно
Решаю пример столбиком, но поменял местами уменьшаемое и вычитаемое (53 — 69)
53
69
——
-16 (калькулятор говорит, что должно получится),
но если считать следуя рассуждениям, то из 3х не вычесть 9 следовательно надо занять единицу из разряда десятков числа 53. Получится 13 — 9 = 4. Далее считаем десятки. Было 5 десятков, стало 4. Из 4х вычесть 6 не получается. Если уйти в отрицательные числа то получится -24 ? Почему не получается -16? где ошибка в рассуждениях? Верно ли я понимаю, что при вычитании столбиком важно, что бы большее число (уменьшаемое) всегда было сверху, а внизу всегда меньшее число (вычитаемое)?
Привет, на сколько я понимаю да, при вычитании это важно
Перепутал два разных действия, вычитание в столбик, и переход в отрицательные числа. Это две разные темы которые нельзя совмещать.
Вычитание в разряде единиц произведено правильно. Но ошибка при вычитании в разряде десятков. Следуя правилам вычитания в столбик, нельзя просто из «4» вычесть «6» и получить «- 2».
В соответствии с правилами вычитания в столбик, что бы вычесть большее «6» из меньшего «4», нужно занять из разряда сотен, которого в данном примере не существует.
Однако, предположим, что мы мысленно добавляем в разряд сотен «1», (Что увеличивает наше уменьшаемое «53» на «100»), Теперь мы можем занять из разряда сотен, и нам необходимо продолжить вычитание в столбик. В соответствии с правилами, теперь, мы должны вычесть «6» из «14» и получим «8».
Получится ответ «84».
Однако, теперь из результат «84» необходимо отнять ту сотню, на которую мы увеличили наше уменьшаемое. (но уже без стобика) мы получим результат «-16».
Смотри, у 53 не хватает 16 единиц чтобы он стал 69 (он меньше 69 на 16)
Из-за того что отнимается число больше уменьшаемого, то насколько вычитаемое больше уменьшаемого уходит в «долг»
Например — мне нужно оплатить товар который стоит 69 рублей, а у меня с собой только 53, в итоге я должен занести продавцу еще 16 рублей
Благодарю вас за то что вы делаете. Но этот шаг слишком большой и я думаю лучше было бы его разделить. Особенно для начинающих. Можно было бы разделить на несколько подшагов и добавить больше практики.
Мне 32, целый день ушло на эту тему.) Но, как вы объясняете, мне пока очень нравится.
Раньше до этого урока было легко, а этот оказался труднее, так как у меня есть свой метод решения в уме. Но сложность было не в том, что сложно решать с данным вами предоставленным способом, а просто в голове тикают одни разряды, десятки, единицы и сотни из-за того что урок оказался длинным со спамленными словами, сам запутался..
Сайт отличный , изучаю постепенно. Автору спасибо!
Большое спасибо! Очень понравился урок!
Спасибо большое, очень нравятся Ваши уроки. Мне было не сложно, очень интересно выполнять задания.
Спасибо и Вам!
Большое спасибо за информацию
Мне нравится эти задачи ✌️️ приятно было с вами познакомиться
Изучая эту тему увидел аналогию (ещё один пример) иллюстрирующий парадокс Галилея. Суть вот в чем: количество чисел кратных данному бесконечно. Но мощность этого множества меньше, чем мощность множества натуральных чисел.
Изучая тему делителей и кратности. Не в ту тему кинул комментарий
Yeah Admin i’m glad Спасибо админ Больше спасибо я из Таджикистана Первый лучший сайт!
А тут только геометрия и алгебра в какой части начинается? Или тут только математика (арифметика)
Пример 6. Вычесть из числа 200 число 84 :
это как бы сложно, но и очень легко!!
главное отминусоват (-1)
например:
200(-1)=199
—
84(-1)=83
.
минусуем 1.
199
—
83
…
116
Последний тест жесть, в уме столько цифр держать мне сложно
У меня немного другой подход к решению этих задач но было очень интересно
Вообще кайф от души, удовольствие получил и знания тоже! Благодарю.
Едем дальше;)
Благодарю разработчиков и создателей . Я благодаря вашим урокам открыл в себе желание познавать математику с нуля. У меня всегда с ней были сложности . И сейчас мне приходиться по не несколько раз прочитывать материал и решать задачи . Но сегодня в отличии от школы я это делаю с удовольствием и главное эти знания я смогу использовать в моей профессиональной деятельности.
WHAAAAAAAAAT!?!?!?!?!?!?!
Наконец-то научился считать впервые за свои 20 лет
мне кажется нужно за одно не только учить то что есть а создавать что-то своё
На деле очень глубокая для понимания тема. Я во многом полагаюсь на интуицию при расчётах, и этот урок указал на опасность такого подхода.