В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем — к тому что падают самолёты, зависают компьютеры, крыши домов улетают из-за сильного ветра, качество связи снижается, а также происходят другие нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства всем знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего обучения.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется.
Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — снова получите семёрку:
5 + 2 = 7
2 + 5 = 7
Если на одну чашу весов положить пакет, в котором 10 килограмм яблок, и на другую чашу так же положить пакет, в котором 10 килограмм яблок, то весы выровнятся, и не важно что яблоки в пакетах лежат вразброс.
Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не измéнится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
5 + 2 = 2 + 5
7 = 7
Полагаем что вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
a + b = b + a
Записанный переместительный закон сложения будет работать для любых чисел.
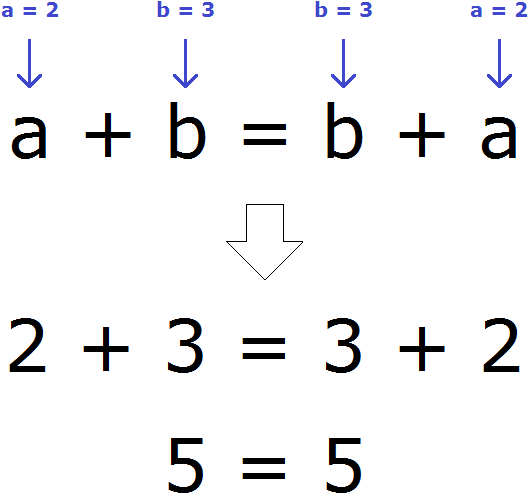
Например, возьмём любые два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отпрáвятся в главное выражение a + b = b + a и подстáвятся куда надо. Число 2 подстáвится вместо а, число 3 — вместо b
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
5 × 2 = 10
2 × 5 = 10
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
10 = 10
Запишем переместительный закон умножения с помощью переменных:
a × b = b × a
Для записи законов в качестве переменных необязательно использовать именно буквы a и b. Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
x × y = y × x
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
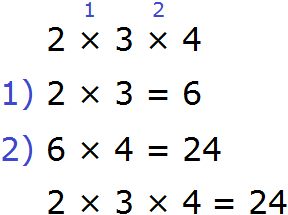
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
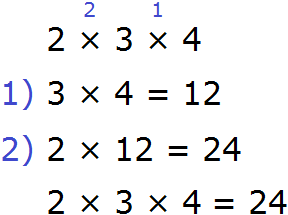
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
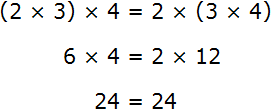
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
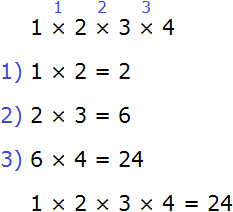
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
(3 + 5) × 2
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
(3 + 5) = 8
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
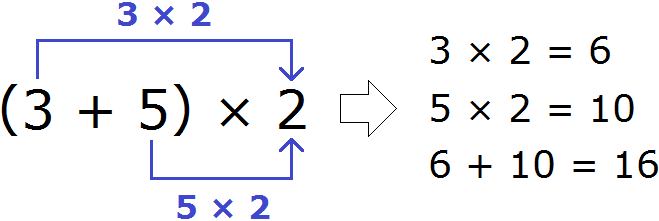
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
Или ещё короче:
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
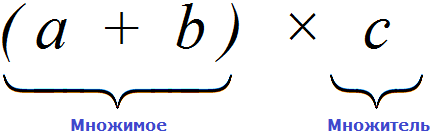
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7
Задания для самостоятельного решения
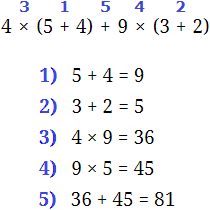
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Наконец-то нашла самый идеальный сайт , но нет продолжения. Пожалуйста не останавливайтесь на этом. Вы мне так нужны!
Спасибо, Алия!
Да, новые уроки в процессе создания. Скоро они будут размещены на сайте.
Спасибо. Продолжаю заниматься. Удачи и добра вам. Терпения и усидчивости мне.
ребята ! огроменнейшее спасибо, вы просто герои. во времена тотального невежества ваш сайт просто спасательный круг. не бросайте нас. с бесконечным уважением ваш почитатель Блохин Сергей
Полностью с вами согласен, Сергей и Алия. Сайт замечательный, но для хотя бы уровня ЕГЭ этого мало , здесь только правила до класса 8…
Прошу прокачать уроки примерно до этого уровня, дальше конечно по вашему желанию!)
Админу огромное спасибо ,выучил фундамент за пол часа ,хотя сам не увлекался математикой ,и в правду останавливайтесь
Добавьте больше практики в ваши уроки.
Спасибо со школы не помню ничего,а ребенку нужна помощь плавает ,здесь все четко,кратно и ясно ,ребят спасибо,если будет продолжение,цены вам не будет,всех благ вам,ждем продолжения
Мне тоже повезло математику с 0 встретить… очень рада. Супер! Спасибо!
Я с вами согласен +++
Приветствую.объясняют всё очень доходчиво. Спасибо!
Спасибо большое теперь у меня есть шанс сдать ЕГЭ
Сдал))), как жизнь:?
О мой гот кто то с 2017 кто то с 2020 я вообще с 2022
2023
2024
ура
2025 здрасте
Замечательный сайт!
Всё подробно и понятно расписано. Продолжайте в том же духе, нужно больше информации.
Сайт просто великолепен!) Спасибо огромное, цели большие
Ещё пожалуйста!
Спасибо! admin
Спасибо большое . Лучший сайт . Готовлюсь к поступлению в универ . Учу математику с нуля. Спасаете . Ещё раз спасибо . Буду ждать новые уроки
Спасибо! Математика нужна всегда и везде! Очень доходчиво объясняете!
Спасибо вам огромное,мне скоро поступать на программиста,а математика очень необходима,так как только с ней проблема, спасибо вам огромное,не останавливайтесь,вы очень нам нужны.
P.S а почему бы вам не оставить свои кошельки на сайте? Думаю,многие люди смогут так вас отблагодарить за ваш труд.
СПАСИБО!!!
Огромное человеческое спасибо Вам! Вы делаете большое и очень доброе дело.
Спасибо этот сайт мне очень помог
Так как мне скоро задавать ЕГЕ
Тут я остановлюсь.Слишком сложно для новичка.Вы детально не объясняете.
Мовсар вы не правы зачем обижаете человека очень доходчиво и четко и понятно все пишет,долгих вам лет жизни многоуважаемый составитель сайта.
Скажите пожалуйста из чего вытекают законы порядка действий? Почему, например, сначала выполняются действия умножения или деления, а только потом сложения и вычитания для выражений? Это вытекает из самих законов математики? Тогда где можно найти математическое обоснование этому? Или просто так договорились люди?
вытекает из самой физики. механики над конкретными предметами — неверите? проверьте сами
Разобрался)))
162/26*2 В данном случаи, что с начало выполняется деление или умножение?
деление
по порядку слева направо
Я бы добавил названия законов — дистрибутивный, коммутативный, ассоциативный. В физмат шуолах дают именно эти названия. Мне нравится идея проекта — не подстраиваться под учебники, программы. Давайте пожалуйста максимально полную, избыточную информацию. Также иногда хочется прочитать интересные истории. Кто это придумал, как считали до этого? Как менялась запись со временем?
Очень доходчиво и простым способом обясняете! Сайт супер! Продолжайте в том же духе! Спасибо Вам и всех благ!!!
Может ли в ЕГЕ помочь?
Спасибо вам огромное за сайт,пожалуйста не останавливайтесь на этом,желаю вам счастье и удачи во всех ваших делах.
извините, сайт конечно очень крут. Но, не могли бы, вы добавить уроки по тригонометрия? Заранее, спасибо.
отличный сайт)спасибо!
отлично!!! ВСЕ СУПЕР!! спасибо автору , весьма понятно и очень удобно … С нетерпением жду новых уроков.ПОБЫСТРЕЕЕЕ!!!
Дорогой автор! Подскажите,пожалуйста,какой — нибудь ресурс,подобный вашему, для изучения геометрии с нуля.
Здравствуйте, Анна!
К сожалению, я не знаю есть ли ресурс на котором можно изучать геометрию.
Могу только посоветовать школьные учебники Киселева и Погорелова.
Здравствуйте! Admin, подскажите пожалуйста, учебники каких авторов Вы рекомендуете для изучения математики?
Здравствуйте. Учебники Киселева и Погорелова
Что значит «переместительно свойство»?
И ещё вопрос.
Почему «множимое»? Почему не «первый множитель» и «второй множитель»? У нас в школе так.
Разницы нету. Множимое и множитель вместе называются сомножителями. Просто на начальных этапах изучения математики удобно первый сомножитель называть множимым. Подробно об этом написано здесь в теме «запись выражений содержащих умножение и деление».
Спасибо большое.
отличный сайт, спасибо вам ребята )))
Этот сайт мне очень помог спасибо разрабртчикам
Спасибо большое за ваш труд ребята!! Отличный сайт!!
Всегда был с математикой и алгеброй на «вы», теперь же, благодаря вам, все больше на «ты». Ну очень подробно и понятно, школьные учителя — «отдыхают».
Спас-ибо вам огромное!
Приятный и продуманный сайт, очень помог!
Спасибо большое!
Удачи Вам!
Тупые законы, ни о чем, ничто не развивают, в советское время было 2 закона: от перемены мест слагаемых сумма не изменяется, также и с умножением, в скобках действие выполняют первым, и ВСЕ, от этого плясали, развивали самостоятельное мышление, творчество.
С Вами согласен! В матем. Самый верный путь тот, что короче. Все тривиальное облепили водой.
Чем законы в советское время отличаются от современных законов?
Хороший сайт.Настоятельно рекомендую всем!
Я возможно ошибаюсь, но пропущен второй раздел про умножение (сочетательный закон).
Не ошиблись. Тема действительно отсутствует. Дело в том, что этот урок еще не закончен. Нужно дополнить его некоторыми вещами и заданиями для самостоятельного решения.
А где же описание сочетательного закона умножения? Переместительный описан, распределительный описан, а сочетательный — нет. Дополните, пожалуйста урок. Спасибо.
Огромное СПАСИБО. Нигде не мог найти такой сайт или книгу где всё так хорошо объясняют. Если и находил, то там были только формулы и способы их решения, объяснения принципов вычисления выражений равнялись 0.
Когда создам свой сайт, в благодарность за ваши труды выложу ссылки на ваш♦☻♦
Админ, если это возможно: поставь кнопки на следующий\ предыдущий урок перед коментами, а не после, я понимаю что есть за и против этого, но хочется поглощать информацию базовых уроков линейно, не отвлекаясь на коменты.
Спасибо большое, всё чётко и грамотно показано и объяснино 😉
Спасибо Админу!просто нет слов!
Формулировка распределительного закона умножения:
Распределительный закон умножения позволяет умножить сумму на число или число на сумму,
мягко говоря расплывчата, а по существу неправильна.
Скорее будет верна формулировка:
Распределительный закон умножения позволяет вместо умножения суммы на число, умножить каждое слагаемое по отдельности на число, после чего результат сложить
Спасибо.
О, спасибо за сайт!!! Помогаю ребенку в начальном образовании!!!
Пожалуйста, давайте продолжение! Автор, вы самый лучший! Желаю вам всего наилучшего!
Просто класс!
Дожился! Программист учит математику с нуля 🙂
Этот сайт много мне помог, я начал изучать данный предмет и очень не хватало такого материала, тут всё по полочкам. За всё время это первый такой сайт. Очень благодарен то что он есть,спасибо разроботчикам. Надеюсь он будет в бесплатном виде и дальше когда будет ещё больше материала.
Это та самая математика для умно-ленивых гуманитариев. Невероятно подобран материал, отличная последовательность и «разжевано» досконально. Где можно донатнуть?
Спасибо! Не стóит донатить)
Почему не стоит?
Разве распределительный закон умножения не нарушает предыдущюю тему — порядок действий?
Спасибо вам за труды, этот сайт то что давно искал, запущенна математика с 5го класса, а мне далеко за 30, буду наверстывать потихоньку, вы главное не прерывайте процесс пожалуйста.
Пожалуйста, скажите в чем разница между переместительным и сочетательным законом
Спасибо, я уже понял
Спасибо Вам огромное за то, что просвещаете мою невежественную голову!
Вы так и не показали почему (a + b)с = aс + bс, а точнее, надо было доказать. Я то знаю и могу обьяснить, а многие не знают. Я даже на работе своим сотрудникам инженерам-конструкторам задал этот вопрос, они не могли ответить, пока я им не объяснил.
в распредилительном законе умножения разве не доказано?
Объясняли бы в школе так! Иногда такое чувство, то что учебники в школах специально написаны что бы их плохо понимали или пишут лишнюю информацию.
Здравствуйте, благодарю за отличный сайт. Хотел узнать будут ли уроки по тригометрии? Очень нужно.
Здравствуйте! Спасибо вам, сайт очень классный. В математике не особо шарю, но тут реально доходчиво объясняется.
Спасибо Вам огромное.
Большое спасибо создателям уроков! Я сейчас в 7 классе и для повторения всех тем этот сайт подходит просто идеально, все понятно и доходчиво♡
спасибо за сайт я здесь даже не читаю правила просто на образец примеров и становится все ясно. спасибо большое
Meni magisterlik disertatdiyam mavzusi matematik qonuniyatlarga doir masalalar yechish deyilgan mavzu edi qòshimcha manba topdim agar shu mavzuda Yana qanday ma’lumotlar izlasam bòladi
Boshlanģich sinflarda matematik qonuniyatlarga doir masalalar yechish
Огромное спасибо! Благодаря вам я стала лучше понимать математику и даже полюбила её.
Сайт потрясающий! Помогает (бесплатно!) освоить практически всю школьную программу, начиная с самого 1 класса. Настолько понятно объяснено, что проходишь темы на раз. Создатели этого замечательного сайта – здоровья вам всем и благополучия!